华为2016暑假实习机试题
华为技术岗上机测试有三道编程题,总体难度偏简单,题目的质量一般。我指的一般,并不是说难度不高就代表不好,只是hw机试题部分题目说得比较模糊,有歧义,以至于我和同学后面讨论的时候发现他原先bug百出的代码也照样能ac全部testcase。
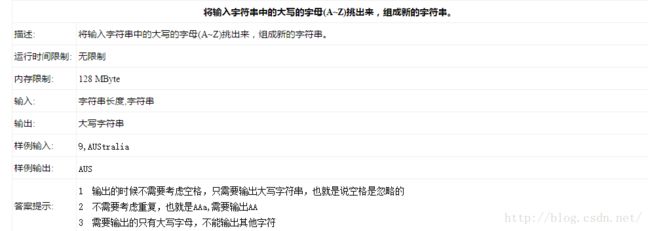
第一题、字符串处理
最简单的做法就是无需考虑输入要求,直接把两个变量当作一行数据存储,然后将其中的大写字符输出。
#include <iostream>
#include <string>
using namespace std;
int main() {
string str;
cin >> str;
int len = str.size();
for (int i = 0; i < len; ++i)
if (str[i] <= 'Z' && str[i] >= 'A')
cout << str[i];
}
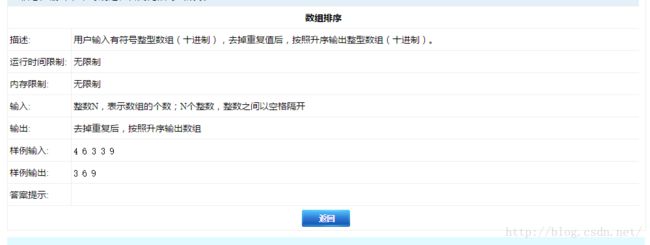
第二题、排序
直接排序,然后输出的时候加入当前元素与上一个元素不同时,才输出该元素。感觉hw的机试有点点小坑就在这里,以往做oj题,基本都是multiple case直至自己用Ctrl+Z终止程序,于是这道题也是这样的做法,但发现最后一个测试用例总是过不了,最后修改一下用只有一次测试用例的做法,AC了。
#include <iostream>
using namespace std;
int cmp(const void* a, const void* b) {
return (*(int*)a - *(int*)b);
}
int main() {
int n, i;
cin >> n;
if (n <= 0) return 1;
if (n == 1) {
cin >> n;
cout << n;
return 0;
}
int* arr = new int[n];
for (i = 0; i < n; ++i)
cin >> arr[i];
qsort(arr, n, sizeof(int), cmp);
cout << arr[0];
for (i = 1; i < n; ++i)
if (arr[i] != arr[i - 1])
cout << " " << arr[i];
}
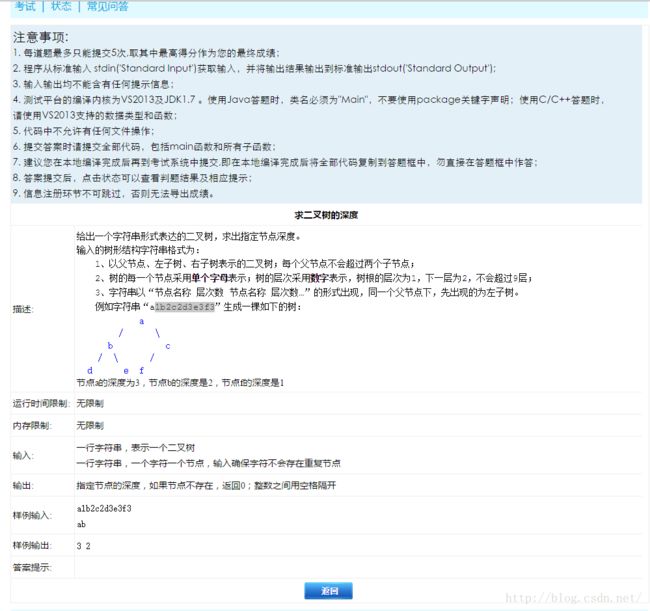
第三题、树
前面两道题都是在几分钟内可以搞定的,这道题比较花时间。通过分析,题目中每一层如果有多个节点都是按照从左到右排布,虽然不是完全二叉树,但是可以看成是完全二叉树通过剪枝得到,因此完全二叉树的所有性质完全符合。我自己的第一种做法是通过建树,然后按照要求输出结果。
#include <iostream>
#include <string>
using namespace std;
struct TreeNode
{
char val;
TreeNode* left;
TreeNode* right;
TreeNode() {};
TreeNode(char val) {
this->val = val;
this->left = this->right = NULL;
}
};
void buildTree(TreeNode*[], int);
int findDepth(TreeNode*[], char);
int getDepth(TreeNode*);
int max(int , int);
int main() {
string tree, nodes;
cin >> tree >> nodes;
int len = tree.size();
//int maxLevel = tree[len - 1] - '0'; // 由于最大层可能不是在最后一个字符,例如a1b2c2d3e3f3和b2c2d3e3f3a1是两棵完全一样的树
int maxLevel = 0;
for (int i = 1; i < len; i += 2) {
if ((tree[i] - '0') > maxLevel)
maxLevel = (tree[i] - '0');
}
TreeNode* trees[512] = {NULL}; // 最大层数为9层
int offset[9] = { 0 };
// 初始化树节点
for (int i = 0; i < len - 1; ++i) {
int level = tree[i + 1] - '0';
int levelBeg = _Pow_int(2, level - 1) - 1; // 每一层的起点为2^(level - 1) - 1
trees[levelBeg + offset[level - 1]] = new TreeNode(tree[i]); // 层数的下标从0开始
offset[level - 1]++;
i++; // 跳过数字
}
// 建树
buildTree(trees, maxLevel);
// 输出每个节点的深度
int test = nodes.size();
for (int i = 0; i < test - 1; ++i) {
cout << findDepth(trees, nodes[i]) << " ";
}
cout << findDepth(trees, nodes[test - 1]) << endl;
}
void buildTree(TreeNode* root[], int maxLevel) {
int total = _Pow_int(2, maxLevel) - 1;
for (int i = total / 2 - 1; i >= 0; --i) {
if (root[i] != NULL) {
root[i]->left = root[2 * i + 1];
root[i]->right = root[2 * i + 2];
}
}
}
int max(int a, int b) {
return a > b ? a : b;
}
int getDepth(TreeNode* root) {
if (root == NULL)
return 0;
return max(getDepth(root->left), getDepth(root->right)) + 1;
}
int findDepth(TreeNode* root[], char ch) {
bool flag = false;
for (int i = 0; i < 512; ++i)
if (root[i] != NULL && root[i]->val == ch)
return getDepth(root[i]);
return 0;
}
上面的代码比如冗余,后来跟同学讨论之后了解到,可以不通过建树来得到节点深度的,或者说用更简单的方式来保留树的结构。依题意,由于一个节点的深度只能从左儿子的深度+1得到,因此可以忽略右儿子情况。另外由于树是完全二叉树的一个剪枝版,节点和左右儿子节点之间的对应关系还在,即假设节点的下标为n,左右儿子的下标分别为2n+1和2n+2,因此如果某一层的节点下标为n,则如果对应的下一层中下标为2n-1为空,则表示无左儿子,也即肯定无右儿子。按照交流后的思路,我code如下,不过没有测试过hw的测试用例,只是自己测试过,不能保证完全正确。
#include <iostream>
#include <string>
using namespace std;
int main() {
string str, testcase;
cin >> str;
cin >> testcase;
// 特殊情况判断
if (str.size() <= 1 || testcase.size() <= 0)
return -1;
int lvl[256];
for (int i = 0; i < 256; ++i)
lvl[i] = 10; // 依题意最大层数不超过9层,且层数从1计起,其他不在树的节点默认为10
int lvlPos[256] = { 0 }; // 记录每个节点在所在层的位置,从1计起
int numPerLvl[11] = { 0 }; // 记录每一层的节点数,最大层数不超过9层,且层数从1计起
int len = str.size();
int tlen = testcase.size();
for (int i = 0; i < len - 1; i += 2) {
// 保留每个节点所在的层数
lvl[str[i]] = str[i + 1] - '0';
// 记录每个节点在所在层偏移的位置,按照完全二叉树的规律,节点的左右儿子为2*n-2, 2*n-1)
lvlPos[str[i]] = ++numPerLvl[lvl[str[i]]];
}
for (int i = 0; i < tlen; ++i) {
// 当节点不在树中,输出0
if (lvl[testcase[i]] == 10) {
cout << 0 << endl;
continue;
}
int depth = 1;
int level = lvl[testcase[i]];
int childNum = lvlPos[testcase[i]];
for (int k = lvl[testcase[i]]; k < 10; ++k) {
// 对于每一层的节点,计算由偏移量得出的儿子数目个数,若少于2*n-1则表示没儿子
childNum = 2 * childNum - 1;
if (numPerLvl[level + 1] < childNum) {
break;
}
else { // 若有儿子,则继续往儿子方向迭代计数
depth++;
level++;
}
}
cout << depth << endl;
}
}