无监督学习

coffe Time

> 类脑计算：根据一个图片进行分类，使用机器学习的方法。使用机器的消耗1000000w 而使用人脑20w。类似于大脑神经元的连接来做识别的硬件。
> Neuron
> Synapse:Digital circuits和Nanotech(memristors忆阻)
> 忆阻：the missing memristor found 
> 机器学习：学习一些参数

原空间问题转化为对偶问题的解，对偶空间的优化问题，（x1,x2）两个空间的内积。
引入核空间的概念，把x转入到另外一个空间。

无监督学习

最简单的情况：用normalized mutual information

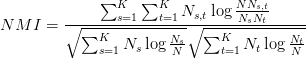
它可以度量同一组数据的两种给标签的方法之间的差异

所以你可以选取有标签的数据来训练，先去掉标签混到一起，用不同的算法聚类，聚类之后再按照聚好的类打上标签，然后分别计算标准标签（就是原来的标签）和聚好类之后的标签之间的差异大小，跟标准标签相差最小的标签就是最好的
问题1：K值选取问题
K的选取通常是我们的目标，也就是说，我们要将这队数据分为几类。因此，是相对明确的。
问题2：初始值的选取问题
初始值的选取对于迭代的结果有较大的影响，选取不当，会出现所有点都归为一类的情况。一个通常的解决方案是：随机选取多组初始值进行分类，选取损失函数最小的分类结果。
编程举例：
将如下三维空间的点进行k-means分类：
[input.txt]
1.0 , 5.7 , 2.8
4.5 , 5.2 , -0.3
-0.9 , 8.1 , 1.4
0.5 , 6.6 , 2.3
3.5 , 4.7 , 0.2
4.7 , 5.9 , -1
5.1 , 8.2 , 0.9
2.1 , 7.4 , 3.0
0.6 , 6.5 , 3.8
在三维空间的图及k-means分类的结果

k-means c++实现

#include <iostream> 
#include <fstream> 
#include <cmath> 
#include <vector> 
#define dim 3//输入特征x的维数 
#define K 2//分类的个数 
#define MAX_NUM 100//读取输入数据的最大数目 
using namespace std;  
//定义类，封装输入向量x,及它要分到哪个类别 
class InputFeature  
{  
public:  
    double x[dim];//保存输入数据的向量坐标 
    int cluster;//标志分类的哪一类(0,1,...,K) 
    InputFeature(double x[dim])//构造函数 
    {  
       memcpy(this->x,x,sizeof(double)*dim);  
       cluster=-1;  
    }  
    //输入函数 
    void print()  
    {  
        cout<<"cluster="<<cluster<<" x=[";  
        for (int i=0;i<dim;i++)  
        {  
            cout<<x[i]<<" ";  
        }  
        cout<<"]"<<endl;  
    }  
    //计算该特征向量与输入向量的2范数(欧式距离) 
    double distanceOf(double u[dim])  
    {  
        double distance=0;  
        for (int i=0;i<dim;i++)  
        {  
            distance+=(u[i]-x[i])*(u[i]-x[i]);  
        }  
        distance=sqrt(distance);  
        return distance;  
    }  
};  
vector<InputFeature> InputVector;//保存输入特征向量 
void inputData()//从文件中读取数据 
{  
    ifstream ifile("input.txt");    
    if(!ifile)    
    {    
        cout<<"input.txt cannot be opened!"<<endl;    
        return;    
    }  
    char ch;    
    int i;  
    for (i=0;i<MAX_NUM;i++)//读取数目 
    {    
        string s_X1,s_X2,s_X3;  
        if(!ifile.get(ch))    
        {  
            return;    
        }    
        while (ch!=',')//读取第一个数据 
        {    
            if (ch==' ')//跳过空格 
            {    
                if(!ifile.get(ch))    
                {  
                    return;    
                }  
                continue;    
            }  
            s_X1+=ch;   
            if(!ifile.get(ch))    
            {  
                return;    
            }    
        }    
        if(!ifile.get(ch))    
        {  
            return;    
        }  
        while (ch!=',')//读取第二个数据 
        {    
            if (ch==' ')    
            {    
                if(!ifile.get(ch))    
                {  
                    return;    
                }  //跳过空格 
                continue;    
            }    
            s_X2+=ch;    
            if(!ifile.get(ch))    
            {  
                return;    
            }     
        }    
        if(!ifile.get(ch))    
        {  
            return;    
        }   
        while(ch!='\n')//读取第三个数据 
        {    
            if (ch==' ')    
            {    
                if(!ifile.get(ch))    
                {  
                    return;    
                }      
                continue;    
            }    
            s_X3+=ch;    
            if(!ifile.get(ch))    
            {  
                cout<<"文件已经读完！"<<endl;    
                return;    
            }     
        }  
        double xt[dim];//将读入的字符串转化为小数 
        xt[0]=atof(s_X1.c_str());  
        xt[1]=atof(s_X2.c_str());  
        xt[2]=atof(s_X3.c_str());  
        InputFeature t1(xt);//生成特征向量 
        InputVector.push_back(t1);//保存到数组 
    }    
    ifile.close();  
}  
//计算在误差err内，2次迭代的结果是否一样 
bool CompareU(double U0[K][dim],double U[K][dim],double err)  
{  
    for (int k=0;k<K;k++)  
    {  
        for (int d=0;d<dim;d++)  
        {  
            if(abs(U0[k][d]-U[k][d])>err)  
            {  
                return false;  
            }  
        }  
   }  
    return true;  
}  
//k-means算法核心 
void k_means(double U[K][dim])  
{  
   double U0[K][dim];  
   memcpy(U0,U,sizeof(double)*K*dim);  
   while (true)  
   {  
       //第一步 标定集合中的点，离哪个U点最近，即将其cluster修改为对应的分类 
       int j;  
       vector<InputFeature>::iterator it;  
       for(it = InputVector.begin(); it != InputVector.end(); ++it)  
       {  
           double dist[K];  
           for (j=0;j<K;j++)//计算该向量到各个标定向量的欧式距离 
           {  
               dist[j]=it->distanceOf(U[j]);  
           }  
           double minDist=dist[0];//初始化最小距离 
           it->cluster=0;//初始化分类 
           for (j=1;j<K;j++)  
           {  
               if (dist[j]<minDist)//如果发现离第j个更近，则更新分类 
               {  
                   minDist=dist[j];  
                   it->cluster=j;  
               }  
           }  
       }  
       //第二步 更新重心U 
       double sum[K][dim],num[K];  
       memset(&sum,0,sizeof(double)*K*dim);  
       memset(&num,0,sizeof(double)*K);  
       for(it = InputVector.begin(); it != InputVector.end(); ++it)  
       {  
           for (int d=0;d<dim;d++)//计算所有相同分类的坐标重心 
           {  
               sum[it->cluster][d]+=it->x[d];  
           }  
           num[it->cluster]++;//计算相同分类的数目 
       }  
       for (j=0;j<K;j++)//更新标定向量的重心 
       {  
           for (int d=0;d<dim;d++)  
           {  
               if (num[j]!=0)  
                 U[j][d]=(sum[j][d])/(num[j]);  
           }  
       }  
       //判断是否收敛， U==U0时收敛 
       if (CompareU(U0,U,1.0e-5))  
       {  
           break;  
       }  
       memcpy(U0,U,sizeof(double)*K*dim);//将本次迭代的结果保存 
   }  
   //输出聚类的结果 
   cout<<"k-means聚类的中心点坐标为："<<endl;  
   for (int k=0;k<K;k++)  
   {  
       cout<<"U"<<k<<"=";  
       for (int d=0;d<dim;d++)  
       {  
           cout<<U[k][d]<<" ";  
       }  
       cout<<endl;  
   }  
   //此时每个元素的分类情况为： 
   cout<<"输入向量的聚类情况及坐标点："<<endl;  
   vector<InputFeature>::iterator it;  
   for(it = InputVector.begin(); it != InputVector.end(); ++it)  
   {  
       it->print();  
   }  
   //计算误差函数 
   double J=0;  
   for(it = InputVector.begin(); it != InputVector.end(); ++it)  
   {  
       J+=it->distanceOf(U[it->cluster]);  
   }  
   cout<<"误差函数J(c,u)="<<J<<endl;  
}  
int main()  
{  
    inputData();//读入输入的数据 
    //初始化K=2个标定向量 
    double U[K][dim]={{4.5,8.1,2.8},{-0.9,4.7,-0.3}};  
    k_means(U);//进行k-means聚类 
    return 0;  
}