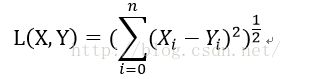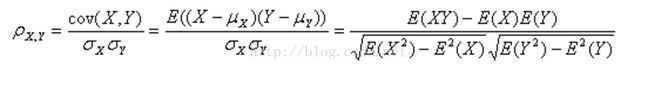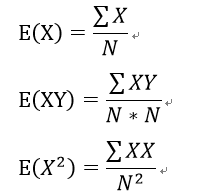《统计学习方法》-KNN笔记和python源码
K近邻法
K近邻法(k-nearest neighbor,k-NN)是一种基本分类与回归方法。
k近邻法实际上利用训练数据集对特征向量空间经行划分,并作为其分类的“模型”。
1.算法:
输入:训练数据集T,其中的实例类别已定。
输出:实例x的所属的类y。
分类时,对新的实例,根据k个最近邻的训练实例的类别,通过多数表决等方式经行预测。
(1)根据给定的距离度量,在训练数据集T中找出与x最近的k个点,涵盖这k个点的x的邻域记作N(x)。
(2)在N(x)中根据分类决策规则决定x的类别y。
2.距离度量方法
(1)欧几里得距离:
(2)皮尔逊距离:
3.k值的选择
如果选择较小的k值,就相当于用较小的领域中的训练实例经行预测,“学习”的近似误差会减小,但缺点估计误差会增大,预测实例对近邻的实例点会非常敏感。
反之亦然。
k-NN的实现:kd树
最简单的实现方法是采用线性扫描,计算耗时巨大。
采用kd树,kd树是二叉树,表示对k维空间的一个划分。构造kd树不断地用垂直于坐标轴的超平面将k维空间划分,构造一系列的k维超矩形区域。
1.构造:
输入:k维数据集T={x1,x2,x3,...xn}
输出:kd树
(1)开始:构造根节点,根节点对应于包含T的k维空间的超矩形区域。
选择xl为坐标轴,以T中所有实例的xl坐标的中位数为切分点,将根节点对应的超矩形区域切分为两个子域。切分由通过切分点并与坐标轴xl垂直的超平面实现。
由根节点生成深度为1的左右子结点:左结点对应于坐标xl小于切分点的子区域,右子结点对应于坐标xl大于切分点的区域。
将落在切分超平面的实例点保存在根结点。
(2)重复:对深度为j的结点,选择xl为切分的周坐标,l=j(modk)+1,以该结点的区域中的所有实例的xl坐标的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域,切分由通过切分点并且与坐标轴xl垂直的超平面实现。
由根节点生成深度为1的左右子结点:左结点对应于坐标xl小于切分点的子区域,右子结点对应于坐标xl大于切分点的区域。
将落在切分超平面的实例点保存在该结点。
(3)直到两个子域没有实例存在时停止。从而形成kd树的区域划分。
2.kd树搜索
# coding=utf-8
# author=altman
class BinaryTree(object):
'''
创建结点
'''
class __node(object):
def __init__(self, value, k,left=None, right=None):
self.value = value
self.left = left
self.right = right
self.s = k
def getValue(self):
return self.value
def setValue(self, value):
self.value = value
def getLeft(self):
return self.left
def getRight(self):
return self.right
def setLeft(self, newLeft):
self.left = newLeft
def setRight(self, newRight):
self.right = newRight
def getS(self):
return self.s
def __iter__(self):
if self.left != None:
for elem in self.left:
yield elem
yield self.value
if self.right != None:
for elem in self.right:
yield elem
'''
创建根
'''
def __init__(self,length):
self.length = length
self.root = None
def insert(self, value):
k = 0
length = self.length
def __insert(k,root, value):
index = k%length
k +=1
if root == None:
return BinaryTree.__node(value,index)
if value[index] < root.getValue()[index]:
root.setLeft(__insert(k,root.getLeft(), value))
else:
root.setRight(__insert(k,root.getRight(), value))
return root
self.root = __insert(k,self.root,value)
def __iter__(self):
if self.root != None:
return self.root.__iter__()
else:
return [].__iter__()
def main():
pass
if __name__ == '__main__':
main()构建和查询
import numpy as np
import binarayTree as bt
import copy as cp
import stack as st
def sim_distance(item1,item2):
diff = (item1-item2)**2
sum_diff = np.sum(diff)
sqrt = sum_diff**0.5
return sqrt
#递归插入
def insertRecursively(k,tree,testArray,length,start,stop):
if start>=stop:
return
middleIndex = (start+stop)//2
count = k%length
tmp = testArray[start:stop,count]
#排序
sortedId = tmp.argsort()
nextArray = cp.deepcopy(testArray)
for i,x in enumerate(sortedId):
nextArray[i+start] = testArray[x+start]
value = (nextArray[middleIndex])
tree.insert(value)
k +=1
insertRecursively(k,tree,nextArray,length,start,middleIndex)
insertRecursively(k,tree,nextArray,length,middleIndex+1,stop)
#创建kd树
def makeTree(tree,testArray):
k = 0
length = testArray.shape[1]
insertRecursively(k,tree,testArray,length,0,len(testArray))
#寻找当前最近点
def findNode(tree,goal,length):
root = tree.root
k = 0
value = root.getValue()
#最小距离
max_distance = 0.0
min_distance = 0.0
#通过栈保存搜索路径
path = st.Stack()
while True:
index = k%length
value = root.getValue()
path.push(root)
k +=1
if goal[index]<root.getValue()[index]:
if root.getLeft()!=None:
root = root.getLeft()
else:
max_distance = sim_distance(goal,value)
nearest = value
break
else:
if root.getRight()!=None:
root = root.getRight()
else:
max_distance = sim_distance(goal,value)
nearest = value
break
min_distance = cp.deepcopy(max_distance)
path.pop()
while not path.isEmpty():
print(nearest)
back_point = path.pop()
index = back_point.getS()
value = back_point.getValue()
tmp_dis = sim_distance(goal[index],value[index])
#判断进入子结点
if tmp_dis <= max_distance:
kd_point = None
if goal[index] < value[index]:
kd_point = back_point.getRight()
if kd_point != None:
path.push(kd_point)
else:
kd_point = back_point.getLeft()
if kd_point != None:
path.push(kd_point)
#判断是否与当前结点,距离更近
tmp_dis = sim_distance(goal,value)
if min_distance >= tmp_dis:
min_distance = tmp_dis
nearest = value
print(nearest)
def main():
testNum = [2,3,5,4,9,6,4,7,8,1,7,2]
goal = np.array([7,2])
testArray = np.reshape(testNum,(6,2))
tree = bt.BinaryTree(2)
makeTree(tree,testArray)
findNode(tree,goal,len(goal))
if __name__ == '__main__':
main()