LCA在线算法ST算法
求LCA(最近公共祖先)的算法有好多,按在线和离线分为在线算法和离线算法。
离线算法有基于搜索的Tarjan算法较优,而在线算法则是基于dp的ST算法较优。
首先说一下ST算法。
这个算法是基于RMQ(区间最大最小值编号)的,不懂的可以这里学习一些
而求LCA就是把树通过深搜得到一个序列,然后转化为求区间的最小编号。
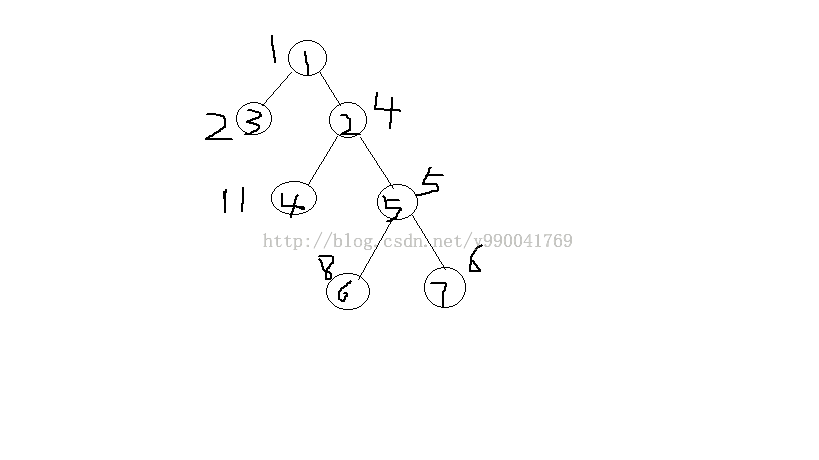
比如说给出这样一棵树。
我们通过深搜可以得到这样一个序列:
节点ver 1 3 1 2 5 7 5 6 5 2 4 2 1 (先右后左)
深度R 1 2 1 2 3 4 3 4 3 2 3 2 1
首位first 1 4 2 11 5 8 6
那么我们就可以这样写深搜函数
int tot,head[N],ver[2*N],R[2*N],first[N],dir[N];
//ver:节点编号 R:深度 first:点编号位置 dir:距离
void dfs(int u ,int dep)
{
vis[u] = true; ver[++tot] = u; first[u] = tot; R[tot] = dep;
for(int k=head[u]; k!=-1; k=e[k].next)
if( !vis[e[k].v] )
{
int v = e[k].v , w = e[k].w;
dir[v] = dir[u] + w;
dfs(v,dep+1);
ver[++tot] = u; R[tot] = dep;
}
}
搜索得到序列之后假如我们想求4 和 7的 LCA
那么我们找4和7在序列中的位置通过first 数组查找发现在6---11
即7 5 6 5 2 4 在上面图上找发现正好是以2为根的子树。而我们只要找到其中一个深度最小的编号就可以了、
这时候我们就用到了RMQ算法。
维护一个dp数组保存其区间深度最小的下标,查找的时候返回就可以了。
比如上面我们找到深度最小的为2点,返回其编号10即可。
这部分不会的可以根据上面链接研究一些RMQ
代码可以这样写:
void ST(int n)
{
for(int i=1;i<=n;i++)
dp[i][0] = i;
for(int j=1;(1<<j)<=n;j++)
{
for(int i=1;i+(1<<j)-1<=n;i++)
{
int a = dp[i][j-1] , b = dp[i+(1<<(j-1))][j-1];
dp[i][j] = R[a]<R[b]?a:b;
}
}
}
//中间部分是交叉的。
int RMQ(int l,int r)
{
int k=0;
while((1<<(k+1))<=r-l+1)
k++;
int a = dp[l][k], b = dp[r-(1<<k)+1][k]; //保存的是编号
return R[a]<R[b]?a:b;
}
int LCA(int u ,int v)
{
int x = first[u] , y = first[v];
if(x > y) swap(x,y);
int res = RMQ(x,y);
return ver[res];
}
那么接下来的应该不是问题了。
上一个题目hdoj 2586 的AC代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
//#pragma comment(linker, "/STACK:102400000,102400000") //不需要申请系统栈
const int N = 40010;
const int M = 25;
int dp[2*N][M]; //这个数组记得开到2*N,因为遍历后序列长度为2*n-1
bool vis[N];
struct edge
{
int u,v,w,next;
}e[2*N];
int tot,head[N];
inline void add(int u ,int v ,int w ,int &k)
{
e[k].u = u; e[k].v = v; e[k].w = w;
e[k].next = head[u]; head[u] = k++;
u = u^v; v = u^v; u = u^v;
e[k].u = u; e[k].v = v; e[k].w = w;
e[k].next = head[u]; head[u] = k++;
}
int ver[2*N],R[2*N],first[N],dir[N];
//ver:节点编号 R:深度 first:点编号位置 dir:距离
void dfs(int u ,int dep)
{
vis[u] = true; ver[++tot] = u; first[u] = tot; R[tot] = dep;
for(int k=head[u]; k!=-1; k=e[k].next)
if( !vis[e[k].v] )
{
int v = e[k].v , w = e[k].w;
dir[v] = dir[u] + w;
dfs(v,dep+1);
ver[++tot] = u; R[tot] = dep;
}
}
void ST(int n)
{
for(int i=1;i<=n;i++)
dp[i][0] = i;
for(int j=1;(1<<j)<=n;j++)
{
for(int i=1;i+(1<<j)-1<=n;i++)
{
int a = dp[i][j-1] , b = dp[i+(1<<(j-1))][j-1];
dp[i][j] = R[a]<R[b]?a:b;
}
}
}
//中间部分是交叉的。
int RMQ(int l,int r)
{
int k=0;
while((1<<(k+1))<=r-l+1)
k++;
int a = dp[l][k], b = dp[r-(1<<k)+1][k]; //保存的是编号
return R[a]<R[b]?a:b;
}
int LCA(int u ,int v)
{
int x = first[u] , y = first[v];
if(x > y) swap(x,y);
int res = RMQ(x,y);
return ver[res];
}
int main()
{
//freopen("Input.txt","r",stdin);
//freopen("Out.txt","w",stdout);
int cas;
scanf("%d",&cas);
while(cas--)
{
int n,q,num = 0;
scanf("%d%d",&n,&q);
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
for(int i=1; i<n; i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w,num);
}
tot = 0; dir[1] = 0;
dfs(1,1);
/*printf("节点ver "); for(int i=1; i<=2*n-1; i++) printf("%d ",ver[i]); cout << endl;
printf("深度R "); for(int i=1; i<=2*n-1; i++) printf("%d ",R[i]); cout << endl;
printf("首位first "); for(int i=1; i<=n; i++) printf("%d ",first[i]); cout << endl;
printf("距离dir "); for(int i=1; i<=n; i++) printf("%d ",dir[i]); cout << endl;*/
ST(2*n-1);
while(q--)
{
int u,v;
scanf("%d%d",&u,&v);
int lca = LCA(u,v);
printf("%d\n",dir[u] + dir[v] - 2*dir[lca]);
}
}
return 0;
}