直线hough变换原理及实现
看了一天的hough变换,总算是有些眉目。一开始总是纠结于hough变换把图像中的点映射到另一个参考系中的直线中,是怎么实现的。即我怎么知道图像中的点事映射到哪些直线中的。。。。。后面终于明白,其做法是将映射到另一个参考系的直线离散化,通过求直线上每个点,来构成直线,从而表达出原图像此点所在的所有直线。至于最后是选择映射到极坐标系中是因为减少运算量。本来无边无际的直线,都可以用有边有界的模和角度来表示。
Hough 变换是基于点-线的对偶性思想。
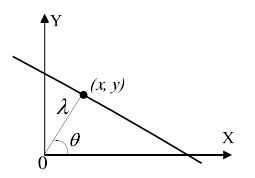
在图像 XY 里,所有过点(x ,y)的直线的方程为
y = px + q (1)
其中 p 为斜率, q为截距,它也可以改写成如式(2)的形式:
q = −px+ y (2)
式(2)可以看作为参数空间 PQ 中过点(p ,q)的一条直线。
如图下所示,在图像空间中 XY 中过点(xi , yi)的直线方程可以写成yi=pxi+q,也可以写成q=-pxi+yi,后者表示在参数空间PQ中的一条直线。同理对于(xj , yj)也可以写成上式形式。如下图:
由此可知,在图像空间中共线的点对应在参数空间里面相交的线,反过来,在参数空间里面相交于同一个点的所有直线在图像空间里面都有共线的点与之对应,这就是点-线的对偶性。
Hough 变换就是根据这样的关系把空间里面的检测问题转换到参数空间,通过参数空间里面进行简单的累计统计来完成直线的检测任务。
在运算式(2)直线方程时候,如果直线接近竖直方向,则会由于p的值都接近无穷而使得计算量增大,此时我们使用直线的极坐标方程来表示直线,如下图,其方程如式(3) ,
λ=xcosθ+ysinθ (3)
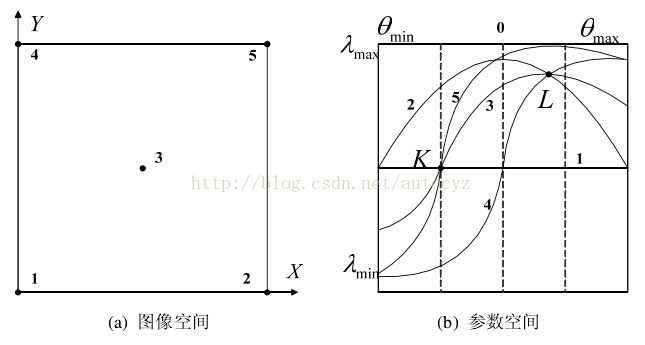
根据这个方程,对于任意一组(λ,θ)都对应一条直线。即原来的点-线对偶性变成了现在的点-正弦曲线对偶性,如图所示,图(a)表示图像空间XY 中的5个点,在图(b)参数空间中对应着5条曲线,这里的θ为[−90 , +90 ],λ的取值范围为 , N为图像的宽度。
, N为图像的宽度。
由图可知,图像空间中各个点可以看作它们在参数空间里面的对应曲线。在图(b)中,曲线 1,3,5 都过 K 点,这表示在图(a)中点 1,3,5 处于同一条直线上,同理,图(a)中点 2,3,4 处于同一条直线上,在图(b)中它们对应的曲线2,3,4 都通过点 L。
Hough 变换的具体实现步骤如下:
(1) 建立一个参数(λ,θ) 空间的二维的数组,该数组相当于一个累加器。
(2) 顺序搜索图像中所有目标(黑色)像素,对于每一个目标像素,在参数空间中根据式(3)找到对应位置,然后在累加器的对应位置加 1。
(3) 求出参数空间(累加器)中最大值,其位置为(λ',θ')。
(4) 通过参数空间位置(λ',θ') ,根据式(3)找到图像空间中相对应的直线参数。
对于直线hough变换过程,可以这么认为。依次遍历图像的所有像素,对每个像素判断是否满足某个特定条件,若满足,则经过该像素的所有直线区域的计数器加1。为了得到经过某个像素的所有直线区域,可以依次用θ的所有可能取值(例如θ可以以1度为增量,从-90度取到+90度),根据(3)式求出λ的值,从而得到很多组(λ,θ),就对应了所有经过此像素的直线。
下面是实现方式:
为避免hough变换程序中多次计算三角函数值,可以采用先用数组存储每个可能的三角函数值,再用查找表的方法查找对应三角函数值,从而提高效率。示例如下:
double sin_value[180];
double cos_value[180];
for(int i=-90; i<90; i++)
{
sin_value[i+90] = sin(i*3.1415926/180);
cos_value[i+90] = cos(i*3.1415926/180);
}
Hough变换的主要流程如下:
for(y=0; y<h; y++) //h为图像和宽度
{
for(x=0; x<w; x++) //w为图像宽度
{
//对θ的所有取值进行计算
for(i=0; i<180; i++)
{
tp = (int)(x*sin_value[i] + y*cos_value[i]);
hough_acc[tp][i] += 1;
}
}
}
上面只是简单的计算流程,在实际应用中,可以根据像素点的灰度值、像素点的范围等来判断是否计算当前点对应的所有(λ,θ)