数据结构_线性表_顺序存储之1顺序栈2共享栈_链式存储之链栈_栈的应用举例
1>//栈是先进后出,后进先出的线性表 简称LIFO线性表
//栈的顺序存储结构成为顺序栈(sequebtial stack).
//顺序栈利用一组地址连的存储单元依次存放从栈底到 栈顶的数据元素,通常用一维数组存放栈的元素
//”指针”top并非指针,而是表示栈顶元素的当前位置
//top不是指针型变量而是整形变量,top=0空栈,top=MaxSize 表示满栈,当top>maxsize 表示栈溢出
代码
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define maxsize (10)
typedef int elemtype;
#pragma mark 定义一个顺序栈
typedef struct stack {
elemtype elem[maxsize];
int top;
}sqstack;
#pragma mark 初始化栈
void InitStack(sqstack*s){
s->top=0;//将顺序栈s置空
}
#pragma mark 判断栈是否为空
bool StackEmpty (sqstack*s){
if (s->top==0) {
printf("空栈");
return false;
}
else {
return true;
}
}
#pragma mark 进栈操作
void push(sqstack*s,elemtype x) {
if (s->top==maxsize) {
printf("栈溢出");
}
else
{
s->elem[s->top++]=x;
}
}
#pragma mark 出栈操作(返回栈顶元素的值)
elemtype Pop(sqstack*s) {
if (s->top==0) {
printf("空栈");
return (elemtype)NULL;
}
else {
s->top--;
return s->elem[s->top];
}
}
#pragma mark 栈深
int Size(sqstack*s) {
return s->top;
}
#pragma mark 取栈顶元素
elemtype Top (sqstack*s){
if (s->top==0) {
printf("空栈");
return (elemtype)NULL;
}
else {
return s->elem[s->top-1];
}
}
#pragma mark 打印取栈中所有元素
void VisitStack(sqstack*s) {
if (s->top==0) {
printf("空栈");
}
else {
for (int i=0; i<s->top; i++) {
printf("%4d",s->elem[i]);
}
}
printf("\n");
}
调用
int main(int argc, const char * argv[]) {
// insert code here...
//void InitStack(sqstack*s); 这样写不会编译出错
sqstack*s;
s=malloc(sizeof(sqstack));
InitStack(s);
for (int i=100; i<110; i++) {
push(s, i);
}
VisitStack(s);
return 0;
}
2>共享栈
//栈使用起来非常方便,但由于要避免栈溢出,就要分配很大的内存的空间,这样就很容易造成空间浪费,当程序同时使用两个栈时,为了提高空间的使用率,可以生成一个共享栈,让两个栈的栈底分别出栈空间的两端,让两个栈各自向空间延伸,当两个栈的栈顶相遇,就表示满栈
typedef struct {
elemtype elem[maxsize];
int top[2];
}dusStack;
//ds 是 dusStack 型变量
//栈1的栈顶有 ds.top[0] 指示,ds.top[0]=0,表示栈1为空
//栈2的栈顶有 ds.top[1] 指示,ds.top[1]=maxsize+1,表示栈2为空
//ds.top[0]+1=ds.top[1] 表示满栈
3>链栈
概述
//顺序栈很有造成存储空间的浪费,而且很多时候不能保证所分配的空间足够使用,这样大大降低了顺序栈的可用性,这时候可以考虑链式存储结构
//栈的链式存储结构称为链栈(linked stack) ,组织结构和单链表相似,链表的尾部结点是栈底,链表的头部结点是栈顶.由于只在链表的头部进行操作,故链栈没有设置头部结点
#pragma mark --链栈的定义
typedef int elemtype;
typedef struct stacknode {
elemtype data;
struct stacknode* next;
}stacknode;
typedef struct {
stacknode*top;
}LinkStack;
#pragma mark --链栈的初始化
void initStack(LinkStack*ls){
ls->top=NULL;//建立一个空栈ls
}
#pragma mark --链栈的进栈操作
void push(LinkStack*ls,elemtype x) {
stacknode*s=NULL;
s=malloc(sizeof(stacknode));//生成新的结点
s->data=x; //结点的数据源赋值
s->next=ls->top; //链入新的结点
ls->top=s; //修改ls栈顶指针
}
#pragma mark --链栈的出栈操作
elemtype Pop (LinkStack*ls) {
stacknode*p=NULL;
elemtype x;
if (ls->top==NULL) {//若栈不为空,删除栈顶的元素并返回元素值,否则返回空元素
return NULL;
}else {
x=(ls->top)->data;
p=ls->top;
ls->top=p->next;
free(p);
return x;
}
}
#pragma mark --链栈的结点值遍历 ,并打印
void visitLinkStack(LinkStack*ls) {
if (ls->top==NULL) {
printf("空栈\n");
return;
}
stacknode*p=ls->top;
while (p) {
printf("%4d\n",p->data);
p=p->next;
}
printf("\n");
}
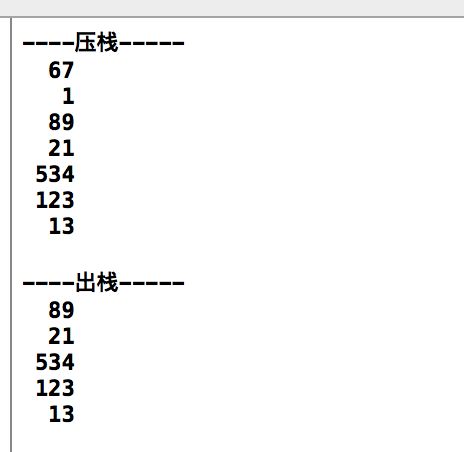
int main(int argc, const char * argv[]) { // insert code here... LinkStack*ls; ls=malloc(sizeof(LinkStack)); initStack(ls); printf("----压栈-----\n"); push(ls, 13); push(ls, 123); push(ls, 534); push(ls, 21); push(ls, 89); push(ls, 1); push(ls, 67); visitLinkStack(ls); printf("----出栈-----\n"); Pop(ls); Pop(ls); visitLinkStack(ls); return 0; } 4>栈的应用举例利用链栈将十进制转换成二进制
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#pragma mark --应用举例1.将十进制转换成二进制输出(采用链栈)
#pragma mark --链栈的定义
typedef int elemtype;
typedef struct stacknode {
elemtype data;
struct stacknode* next;
}stacknode;
typedef struct {
stacknode*top;
}LinkStack;
#pragma mark --链栈的初始化
void initStack(LinkStack*ls){
ls->top=NULL;//建立一个空栈ls
}
#pragma mark --链栈的进栈操作
void push(LinkStack*ls,elemtype x) {
stacknode*s=NULL;
s=malloc(sizeof(stacknode));//生成新的结点
s->data=x; //结点的数据源赋值
s->next=ls->top; //链入新的结点
ls->top=s; //修改ls栈顶指针
}
#pragma mark --链栈的出栈操作
elemtype Pop (LinkStack*ls) {
stacknode*p=NULL;
elemtype x;
if (ls->top==NULL) {//若栈不为空,删除栈顶的元素并返回元素值,否则返回空元素
return NULL;
}else {
x=(ls->top)->data;
p=ls->top;
ls->top=p->next;
free(p);
return x;
}
}
#pragma mark --链栈的结点值遍历 ,并打印
void visitLinkStack(LinkStack*ls) {
if (ls->top==NULL) {
printf("空栈\n");
return;
}
stacknode*p=ls->top;
while (p) {
printf("%d",p->data);
p=p->next;
}
printf("\n");
}
int main(int argc, const char * argv[]) {
// insert code here...
LinkStack*ls;
ls=malloc(sizeof(LinkStack));
initStack(ls);
printf("输入一个要转换的数:\n");
int n;
scanf("%d",&n);
if (n<0) {
printf("要输入正数:");
return 0;
}
if (n==0) {
push(ls, 0);
}
if (n>0) {
while (n) {
push(ls, n%2);
n=n/2;
}
}
visitLinkStack(ls);
return 0;5>栈的逆置合并
#pragma mark --线性表的逆置运算
//设有一个具有n个元素的线性表存放在一个一位数组A[M]前n个数组单元中,编写一个算法,将这个线性表原地逆置
//思路----将最后一个元素变为第一个元素,使ai 编变成ai-1的直接前驱
typedef int elemType;
elemType* inverse(elemType a[],int n) {
elemType t;
for (int i=0; i<=(n-1)/2; i++) {
t=a[i];
a[i]=a[n-i-1];
a[n-i-1]=t;
}
return a;
}
void visit(int a[],int n) {
for (int i=0; i<n; i++) {
printf("%3d",a[i]);
}
printf("\n");
}
//编写一个算法讲一个单链表逆置,要求在原表上进行,不允许重新建链表
//思路:在遍历原表的时候,从原表的第一个结点开始,将各个结点的指针逆转,最后修改头结点的指针域,令其指向原表的最后一个结点,即位新表的第一个结点
typedef int MyInt;
typedef struct node{
MyInt data;
struct node*next;
}Lnode,linkList;
Lnode* initLinklist() {
Lnode*h;
h=malloc(sizeof(Lnode));
h->next=NULL;
return h;
}
void insert(Lnode*p,elemType x) {
Lnode*s;
s=(Lnode*)malloc(sizeof(Lnode));
s->data=x;
s->next=p->next;//核心描述
p->next=s; //核心描述
}
void visitList(Lnode*L) {
if (L==NULL) {
printf("链表不存在\n");
return;
}
Lnode* p=L->next;;
while (p) {
printf("%4d",p->data);
p=p->next;
}
printf("\n");
}
//逆置链表
Lnode* inverseList (Lnode*h) {
Lnode*r,*q,*p;
p=h->next;
if (p==NULL) {
printf("空表,怎么逆置,哥");
return NULL ;
}
if(p->next==NULL) {
printf("链表只有一个结点,怎么逆置");
return NULL;
}
q=p;
// visitList(q);
p=p->next;
// visitList(p);//D C B A
q->next=NULL; //首节点变成了尾结点
// visitList(q); //空
while (p) {
r=p->next;
p->next=q;//逆转指针
//visitList(p);
q=p; //指针迁移
// visitList(q);
p=r;
// printf("r==\n");
// visitList(r);
// printf("p==\n");
// visitList(p);
}
h->next=q; //头指针的h后继是q
return h;
}
//合并有序单链表
//两个按元素值递增的有序排列的单链表A和B归并成一个按元素值递增的有序排列的单链表C.
//指针平行移动,依次扫描完成
//逐一扫描两个表的元素,赋值较小值的数据元素并插入到C的表尾,当两表之一已经到头,赋值另一个表的剩余部分插入到C的表尾
//例如 A=(2,3,6,7,9),B=(1,5,7,23,78,89,900)---->C=(1,2,3,5,7,9,23,78,89,900)
Lnode*hb(Lnode*pa,Lnode*pb) {
Lnode*p,*q,*pc;
pa=pa;
pb=pb;
pc=malloc(sizeof(Lnode));//建立C的头结点PC
p=pc; //将p指向C的头结点
while (pa&&pb) {
q=(Lnode*)malloc(sizeof(Lnode)); //建立新的结点q
if (pb->data<pa->data) { //比较A,B数据域较小的,
q->data=pb->data; //较小的值赋给q的数据域
pb=pb->next; //B的指针后移
}
else{
q->data=pa->data;
pa=pa->next;
}
p->next=q; //将q接在p的后面
p=q; //p始终指向表C当前的尾结点
}
while (pa) { //若A比B长,将A余下的结点连接在C的表尾
q=(Lnode*)malloc(sizeof(Lnode*));
q->data=pa->data;
pa=pa->next;
p->next=q;
p=q;
}
while (pb) { //若B比A长,将B余下的结点连接在C的表尾
q=(Lnode*)malloc(sizeof(Lnode*));
q->data=pb->data;
pb=pb->next;
p->next=q;
p=q;
}
p->next=NULL;//表尾指向空
return pc;
}
6线性表应用举例>一元多项式相加
//一元多项式相加
typedef struct Node {
int coef;//系数域
int exp; //指数域
struct Node*next;//指针域
}JD;
void dxsxj(JD*ha,JD*hb) {
JD*p,*q,*r,*pre;
int x;
p=ha->next;//q和q分别指向多项式的第一个结点
q=hb->next;
pre=ha;//pre 指向多项式A的头结点
while (p&&q) {
if (p->exp==q->exp) {
x=p->coef+q->coef;//系数相加
if(x!=0){
p->coef=x;//和不是0x修改p的系数域
pre=p;
}else {
pre->next=p->next;//和为0,从A中删除P
free(p);//释放结点
}
p=pre->next;
r=q;
q=q->next;
free(r);
}else if (p->exp>q->exp) { //将q插在p之前,q后移,p不动
r=q->next;
q->next=p;
pre->next=q;
pre=q;
q=r;
} else {//p是多项式中的一项,p后移
pre=p;
p=p->next;
}
}
if(q)//若B表长,将B的剩余结点连接到A中
pre->next=q;
free(hb);
}