matlab的parcorr函数

参考文章http://wenku.baidu.com/view/32b8f843fc4ffe473268ab2a.html
零均值的平稳时间序列：
样本自协方差
样本自相关系数函数：
偏相关函数：从中解出的一串
程序如图所示

clear ;
A = [1 2 3 4] ;
n = length(A) ;
[ACF,lags,bounds] = autocorr(A,n-1) ;
% ACF = [1,0.2500,-0.3000,-0.4500]
%构造矩阵[1     0.25    -0.3
%         0.25  1       0.25
%         -0.3  0.25    1    ]
B = [1 0.25 -0.3 ; 0.25 1 0.25 ; -0.3  0.25 1 ] ;
%构造向量[0.25;-0.3;-0.45]
C = ACF(2:4)' ;
%保存 x11 ,x22 ,x33
x = zeros(n-1,1) ;

%计算x11
% [1][x11] = [0.25] ====>x11 = 0.25
x(1,1) = C(1) ;

%计算x22
%[1 0.25 ; 0.25 1][x21 ; x22] = [0.25;-0.3]
temp =  B(1:2,1:2) \ C(1:2) ;
x(2,1) = temp(end) ;

%计算x33
%[1 0.25 -0.3 ; 0.25 1 0.25 ; -0.3 0.25 1][x11;x22;x33] = [0.25;-0.3;-0.45]
temp =  B \ C ;
x(3,1) = temp(end) ;
x = [1;x] ;
subplot(2,1,1) ;
plot([0:n-1],x',[0:n-1],0,'-k',[0:n-1],x','*') ;
title('自己求偏相关') ;

subplot(2,1,2) ;
[PartialACF,lags,bounds] = parcorr(A,n-1) ;
plot(lags,PartialACF,lags,0,'-k',lags,PartialACF,'*') ;
title('parcorr求偏相关') ;

得到的图像如图所示：

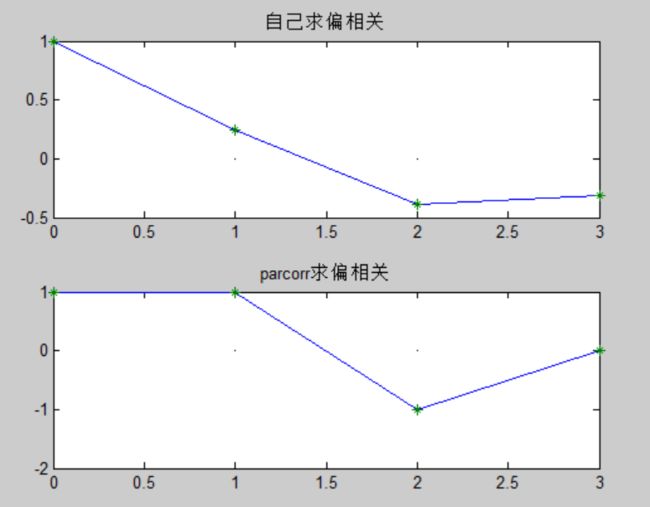
得到的图像不怎么相似，以为自己的错了，然后在上面参考文章里找到了求偏相关函数的程序

clear ;
A = [1 2 3 4] ;
n = length(A) ;

%[ACF,lags,bounds] = autocorr(A,n-1) 
% ACF = 1 0.25 -0.3 -0.45

%求自相关函数
A = A - mean(A) ;
rc = 0 ;
for k = 1 : n
    rc = rc + A(k)*A(k)/n ;
end

for k = 1 : n-1
    x = 0 ;
    for j = 1 : n-k
        x = x + A(j)*A(j+k)/n ;
    end
    r(k) = x ;
    p(k) = r(k) / rc ;
end

x = 1 : n-1 ;
figure;plot(x,p,x,0,'-k',x,p,'*') ;
title('自相关函数') ;

%求偏相关函数m(k,k)
m(1,1) = p(1) ;
for k = 1 : n-2
    x = 0 ;
    y = 0 ;
    for j = 1 : k
        x = x + p(k+1-j) * m(k,j) ;
        y = y + p(j) * m(k,j) ;
    end

    m(k+1,k+1) = (p(k+1)-x) / (1-y) ;

    for j=1 : k
        m(k+1,j) = m(k,j) - m(k+1,k+1)*m(k,k-j+1) ;
    end
end

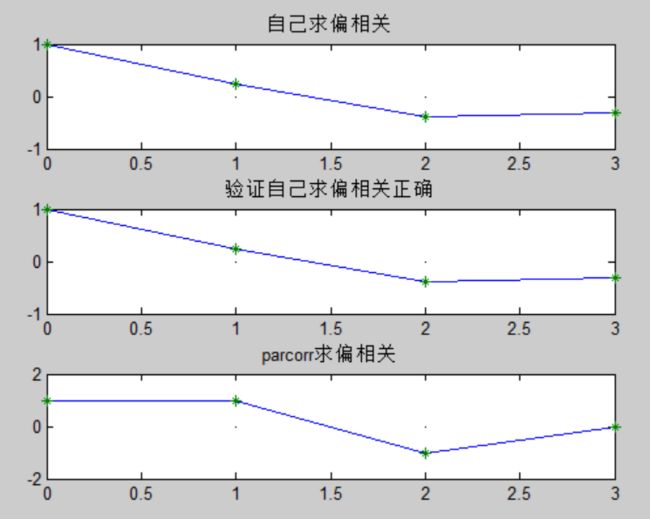
result = [1,(diag(m))'] ; plot([0:n-1],result,[0:n-1],0,'-k',[0:n-1],result,'*') ; axis([0 3 -0.5 1]) ; title('验证自己求偏相关正确') ; 

为了方便对比，我把图像集成到了一起，如图所示：。

为什么自己写的偏相关程序与parcorr函数不一样呢，我也不知道！！！
但是我们可以在序列比较大的情况下再对比一下。

clear ;
z = [15600 8960 10400 10600 10800 9880 9850 10900 8810 9960 ...
    12200 7510 8640 6380 6810 8820 14400 7440 7240 6430 11000 ...
    7340 9260 5290 9130 7480 6980 9650 7260 8750 9900 7310 9040 ...
    7310 8850 7840 10700 6190 9610 7580 9990 6150 8250 6030 8980 ...
    6180 9630 9490 2340 11100 5090 10900 6490 12600 6640 7430 6760 ...
    10000 9300] ;

m = mean(z) ;
for k = 1 : 59
    X(k) = z(k) - m ;
end

%求自相关函数
rc = 0 ;
for k = 1 : 59
    rc = rc + 1/59*X(k)*X(k) ;
end

for k=1:15
    x=0;
    for j=1: 59-k
        x = x + 1/59*X(j)*X(j+k) ;
    end

    r(k) = x ;
    p(k) = r(k) / rc ;
end

x = 1 : 15 ;
figure;plot(x,p,x,0,'-k',x,p,'*') ;
title('自相关函数');


%求偏相关函数m(k,k)
m(1,1) = p(1) ;
for k = 1 : 14
    x = 0 ;
    y = 0 ;
    for j = 1 : k
        x = x + p(k+1-j) * m(k,j) ;
        y = y + p(j) * m(k,j) ;
    end

    m(k+1,k+1) = (p(k+1)-x) / (1-y) ;

    for j = 1 : k 
        m(k+1,j) = m(k,j) - m(k+1,k+1) * m(k,k-j+1) ;
    end
end

result = [1,(diag(m))'] ; x = 0 : 15 ; figure;subplot(2,1,1) ; plot(x,result,x,0,'-k',x,result,'*') ; title('自己求偏相关函数') ; subplot(2,1,2) ; [PartialACF,lags,bounds] = parcorr(z,15) ; plot(lags,PartialACF,lags,0,'-k',lags,PartialACF,'*') ; title('parcorr求偏相关') ;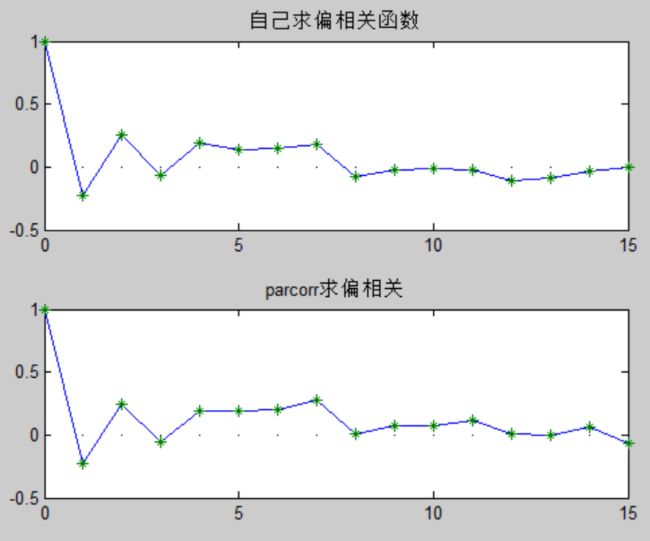

可以看出来，虽然每个具体值还存在偏差，但是整体趋势还是一致的，从而可以说明我们写的偏相关函数是正确的。

既然偏相关函数搞清楚了，我们就了解一下ARMA模型识别
举个例子：

clear ;
z = [15600 8960 10400 10600 10800 9880 9850 10900 8810 9960 ...
    12200 7510 8640 6380 6810 8820 14400 7440 7240 6430 11000 ...
    7340 9260 5290 9130 7480 6980 9650 7260 8750 9900 7310 9040 ...
    7310 8850 7840 10700 6190 9610 7580 9990 6150 8250 6030 8980 ...
    6180 9630 9490 2340 11100 5090 10900 6490 12600 6640 7430 6760 ...
    10000 9300] ;
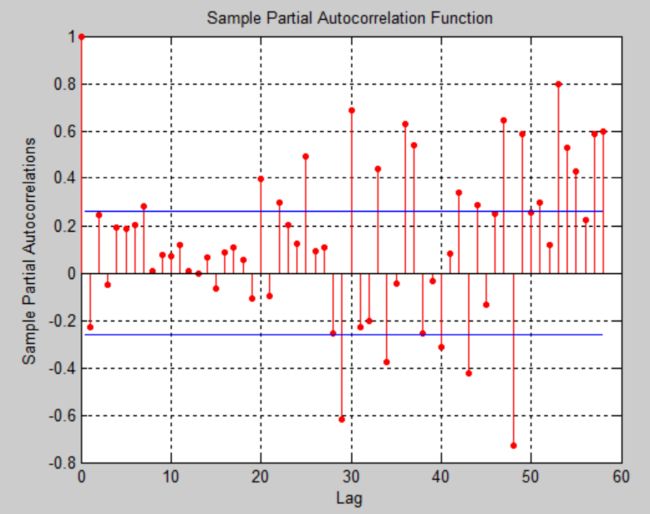
figure ;parcorr(z,length(z)-1) ;

figure ;autocorr(z,length(z)-1) ;

自相关函数如图所示，3阶结尾
偏相关函数如图所示，具有拖尾现象，所以上面的序列可以判断为MA（3）模型