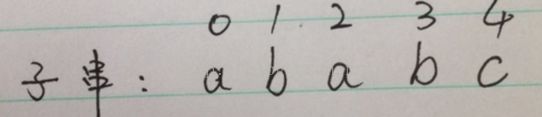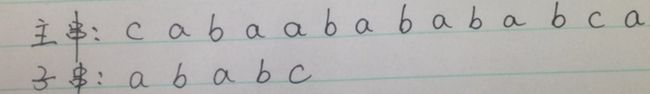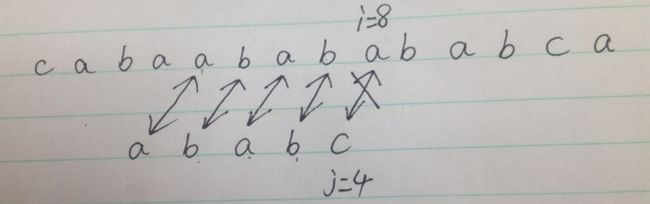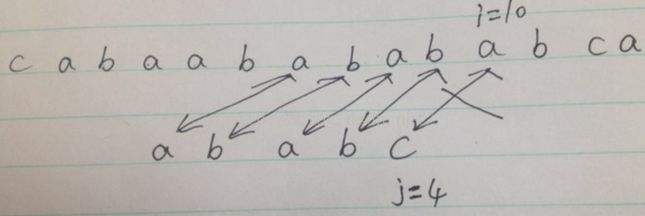串模式匹配——从BF到KMP最精讲

（转载自朋友的博客http://blog.csdn.net/msdnwolaile/article/details/51287911#comments）

看了好多关于KMP算法的书籍和资料，总感觉没有说的很清楚，为什么会产生next数组，为什么给出了那么简短的程序，没有一个过程，而有的帖子虽然next及其字符串匹配说的很清楚，但是推理的一些过程相当复杂，比较抽象，今天在这里简单的提一下我的理解，尽可能的把这个过程讲的简单，容易理解

从模式匹配之初：我们先是研究的是BF算法，鉴于我们经常行的需要回溯，总是做一些无用功，为了提高算法的时间度和空间度，引入了next数组（至于为什么提高时间，下面会提到），也就是采用next数组，我们不需要再去回溯了，可以直接比较，这也就是KMP算法了

所以说：从BF到KMP，只是简单的嫌弃BF算法，花费的时间空间太长太大了而已，一切都在进步！！！

串的模式匹配或者串匹配：

子串的定位操作是找子串在主串中从POS个字符后首次出现的位置

一般将主串S称为目标串，子串T称为模式串

BF算法：

Brute-Force，也称为蛮力（暴力）匹配算法

1，从主串S的第pos个字符开始，和模式串T的第一个字符进行比较，

2，若相等，则逐个比较后续的字符;不然，就回溯到主串的第POS+1个字符开始，继续和模式串T的第一个字符进行比较，反复执行步骤2，知道模式串T中的每一个字符都和主串相等（返回当前主串S匹配上的第一个字符）或者找完主串S(POS位置后的所有字符（返回0）)，

程序1：

 #include <stdio.h>
 #include <string.h>
 #include <malloc.h>

 int BFmode(char *s, char *t, int pos)
 {
         int flag1,flag;
         int i,j;
         int slength, tlength;
         slength = strlen(s);
         tlength = strlen(t);

         for(i = pos; i < slength; i++)
         {
                 flag1 = i,flag = 0;
                 for(j = 0; j < tlength; j++)
                 {
                         if(s[i] == t[j] && i < slength)
                         {
                                 flag ++;
                                 i++;
                         }
                         else
                                 break;
                 }
                 if(flag == tlength)
                 {
                         return flag + 1;
                 }
                 i = flag1;
         }

         return 0;
 }

  int main()
 {
         char s[50];   //目标串
         char t[20];   //模式串同时也是子串
         int pos;
         scanf("%s", s);
         scanf("%s", t);
         scanf("%d", &pos);
         pos = BFmode(s,t, pos);

         printf("POS:%d\n", pos);

         return 0;
 }

编写完了之后，总觉得怪怪的，程序不应该这么复杂啊，

程序2：

 int BFmode(char *s, char *t, int pos)
 {
         int flag1,flag;
         int i,j = 0;
         int slength, tlength;
         slength = strlen(s);
         tlength = strlen(t);

         for(i = pos; i < slength && j < tlength; i++)
         {

                 if(s[i] == t[j])
                 {
                         j++;
                         if(j == tlength)
                                 return i - j + 2;
                 }
                 else
                 {
                         i = i - j;
                         j = 0;
                 }
         }

         return 0;
 }

我们还可以将程序优化一下： 毕竟程序的重点是（时间和空间），

算法比较简单，但是在最坏的情况下，算法的时间复杂度为O(n×m)，n，m分别为主串和模式串的长度。从第一个程序就可以很容易的看出来了，主要时间都耗费在失配后的比较位置有回溯，主要都给拉回来，因而比较次数过多

为了时间都不浪费在主串的回溯上面，那么我们引入了next数组

什么是next数组呢？

1，首先：next数组是针对于子串而言的

      求子串相对的前缀和后缀，看是否相等(相等即退出)，最大的相等个数即就是next的值

           

           如上：上面的数字代表字符在字符数组中的下标

      next[0]:         "a"     (无前缀，无后缀)                             next[0] = 0

      next[1]:         "ab"   ("a"  !=  "b")                                      next[1] = 0

      next[2]:         "aba" ("ab"!="ab", "a" == "a")                     next[2] = 1

      next[3]:         "abab"

                           ("aba" != "bab" , "ab" == "ab")                   next[3] = 2

      next[4]:         "ababc"

                           ("abab" != "babc", "aba" != "abc", "ab" != "bc", "a" != "c")

                                                                                             next[4] = 0

        

      这样求到的next串没有问题，代码也没有问题

      程序：

     

 #include <stdio.h>
 #include <string.h>

 int next[30] = {0};
 int flag;

 int get_2_next(char *p, int current, int flag1) //P为所求的字符串，current为当前的位置，flag1为函数中的移动标志位
 {
         int i,j;
         char p1[30];
         char p2[30];                             //临时数组，便于比较

         if(current == 0)
                 next[0] = 0;                     //因为位置为0的时候，既没有前缀，也没有后缀
         while(flag1 <= current)
         {
                 for(i = 0; i <= current - flag1; i++)
                 {
                         p1[i] = p[i];
                 }
                 p1[i] = '\0';

                 for(i = flag1; i <= current; i++)
                 {
                         p2[i - flag1] = p[i];
                 }
                 p2[i - flag1] = '\0';

                 if(strcmp(p1, p2) == 0)
                 {
                         return strlen(p1);
                 }

                 flag1 ++;
         }

         return 0;
 }

 void get_1_next(char *p, int plength)            //p为所求的字符串，plength为所求字符串的长度
 {
         int i;
         for(i = 0; i < plength; i++)
         {
                 flag = 1;
                 next[i] = get_2_next(p, i, flag);
         }
 }

 int main()
 {
         int i;
         char p[30];
         int plength;

         scanf("%s", p);
         plength = strlen(p);
         get_1_next(p, plength);

         for(i = 0; i < plength; i++)
         {
                 printf("%c:%d\n", p[i], next[i]);
         }
         printf("\n");
 }

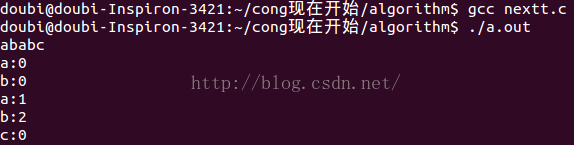
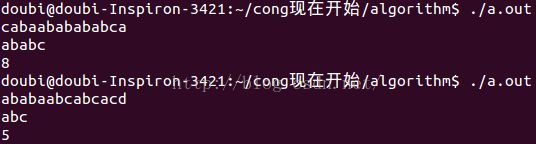
运行结果：

嗯嗯，对，这是我初步的想法，这样求得，但是，但是，但是，翻了翻资料，感觉在时间复杂度和空间复杂度方面太low了，别人的时间空间都是极少的，一定有优化的办法的，一定有

经过长时间的思考，终于想明白了，

哈哈，也就是说，上面的写法做了很多的无用功，

在求后续的next串的时候，完全没有必要去从最大的前缀去求，可以借用之前求到的next

如：串s  =  "ababc"          求next[4]

        由于我们已经知道了，next[3]    =   2,("aba" != "bab" , "ab" == "ab")，所以，我们非常的没有必要去做求

       （“abab”是不是等于“babc”）等等这些判断，因为从之前的next[1] = 0（可以知道“a”不等于“b”，也就是s[1]和s[0]直接的比较），

        所以当前我们要处理的就是：

        1，当前的字符（s[4]  = 'c'）是不是等于next[3]也就是（s[2]）,即就是判断s[2]是不是等于s[4]，如果相等：next[4]  =  next[3] + 1

        2，如果不相等的话，那么我们需要比较的就是s[4]是不是和s[next[next[3]]],由于next[3] = 2,那就是next[2],

              next[2]等于1，那么就是s[4]和s[1]进行比较，判断是否相等，如果相等next[4] = next[2] + 1并且退出;

        3，如果不想等的话，那么需要继续执行类似于我们上面的步骤，当带比较的字符为0的时候，那么就退出

这里：我们是通过next[3]简易的求了一下next[4],当然，这里完全可以通过递归或者循环来求出后面的next数组，因为next[0]是知道的（next[0]没有前缀，也没有后缀，所以说：next[0] = 0），由此，我们就可以求出next[1,2,3,4,....]等等

为了便于理解，我没有采用i，j的说法，觉得那样的话，可能会越说越糊涂

下面是一个简单的程序：

 #include <stdio.h>
 #include <string.h>

 int next[30] = {0};

 void get_1_next(char *p, int plength)            //p为所求的字符串，plength为所求字符串的长度
 {
         int i, j,a;
         next[0] = 0; //没有前缀，也没有后缀
         for(i = 1; i < plength; i++)
         {
                 j = i;
                 while(1)
                 {
                         if(p[next[j - 1]] == p[i])
                         {
                                 next[i] = next[j - 1] + 1;
                                 break;
                         }
                         else if(next[j - 1] == 0)
                         {
                                 next[i] = 0;
                                 break;
                         }
                         else
                         {
                                 a = next[j - 1];   //这两行是为了说明 j = j- 1;（便于循环）
                                 j = a + 1;
                         }
                 }
         }
 }

 int main()
 {
         int i;
         char p[30];
         int plength;

         scanf("%s", p);
         plength = strlen(p);
         get_1_next(p, plength);

         for(i = 0; i < plength; i++)
         {
                 printf("%c:%d\n", p[i], next[i]);
         }
         printf("\n");
 }

运行结果：

通过程序的验证，证明了我们的猜想，也就是说：我们上面说的完全正确，可以大大的削减时间和空间来达到我们的目的，不需要多余占用额外的存储空间，不需要多次循环，不需要做一些无畏的事情

可是，可是，可是？？？有人到这里就会问了，这个和我们所说的KMP有什么关系啊，这个又和我们上面所说的不用回溯又有什么关系啊？？？哈哈哈，这可算是问到重点上了，，，

下面我们讨论一下回溯的问题，以及什么是KMP算法

     
1，先看这个问题（给定一个子串，一个主串，求模式匹配的过程时）

      可以知道的是：

      子串的next数组是：0   0    1    2   0

       主串是从0开始的

       我们开始匹配：

        1，s[0]与t[0]进行比较，如果不想等，那么主串往后移动，如果相等，那么两者一起移动，对于当前的情况是，两者不想等，那么主串后移

          

        2，s[1]与t[0]进行比较，不相等的话，继续主串后移，相等的话，一起移动， 直到两者字符不相等，或者完全匹配后退出，当前的情况是：

        

                可以直观的看到：s[4] != t[3],这里就调用了next，为什么要调用next呢？？？因为前面的部分字符“aba”在主             串和子串中已经完全匹配，为了不用回溯和浪费，也为了保证能保留剩余部分的匹配，故引入了next

                由于已经比较到了t[3]，所以，我们求next[2]的值，然后比较t[next[2]]和s[4](即就是s[4]和t[1])，可以看到

                s[4] != t[1] ,然后继续如上的步骤，比较s[4]和t[next[1]](即就是比较s[4]和s[0]),继续比较：

                1，两者相同，还是以上的步骤，两者整体移动

                2，不同，将主串后移

                当前的情况满足条件1，故s[4] == t[0],继续两者后移

        3，当前的位置如下：

              

              可知：s[8] != t[4],嗯嗯，如上，继续调用next数组：

              比较s[8]和t[next[3]],即就是比较（s[8]和t[2]）,判断两者是否相等，可知，对于上图，两者是相等的，所以此时（i = 8 ， j = 2）,（这里就明显的体现了不用回溯的直接价值啊，哈哈哈），然后，同步后移

          4，当前的状态如下：

                

                同理，还是上面的判断步骤，就可以找到了（完全匹配完成了），然后返回匹配后的第一个值

           

           代码如下：

           

 #include <stdio.h>
 #include <string.h>

 int next[30] = {0};

 void get_1_next(char *t, int tlength)            //p为所求的字符串，plength为所求字符串的长度
 {
         int i, j,a;
         next[0] = 0; //没有前缀，也没有后缀
         for(i = 1; i < tlength; i++)
         {
                 j = i;
                 while(1)
                 {
                         if(t[next[j - 1]] == t[i])
                         {
                                 next[i] = next[j - 1] + 1;
                                 break;
                         }
                         else if(next[j - 1] == 0)
                         {
                                 next[i] = 0;
                                 break;
                         }
                         else
                         {
                                 a = next[j - 1];   //这两行是为了说明 j = j- 1;（便于循环）
                                 j = a + 1;
                         }
                 }
         }
 }

 int get_position(char *s, int slength, char *t, int tlength)
 {
         int i = 0,j = 0;
         int flag = 0, a;
         while(i < slength && j < tlength)
         {
                 if(s[i] == t[j])
                 {
                         i++; j++;
                         flag ++;
                 }
                 else
                 {
                         if(flag == 0)
                                 i++;
                         else
                         {
                                 while(1)
                                 {
                                         if(t[next[j - 1]] == s[i])
                                         {
                                                 j = next[j - 1];
                                                 i++;
                                                 j++;
                                                 break;
                                         }
                                         else if(next[j - 1] == 0)
                                         {
                                                 j = 0; flag = 0; i++;
                                                 break;
                                         }
                                         else
                                         {
                                                 a = next[j - 1]; //这两行是为了说明 j = j- 1;（便于循环）
                                                 j = a + 1;
                                         }
                                 }
                         }
                 }
         }

         return i - tlength;
 }

 int main()
 {
         int position,i;
         char s[30], t[30];      //s为主串，t为子串,返回子串在主串中完全匹配（或者不匹配）后的位置POSITION
         int slength, tlength;

         scanf("%s", s);
         scanf("%s", t);
         slength = strlen(s);
         tlength = strlen(t);
         get_1_next(t, tlength);

         position = get_position(s,slength,t,tlength);
         printf("%d\n", position);
 }

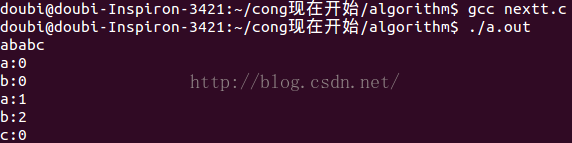
运行结果：

上面的这些也就是所谓的KMP算法了

Knuth-Morris-Pratt算法（简称KMP），是模式匹配中的经典算法，和BF算法相比，KMP算法的不同点是消除BF算法中主串S指针回溯的情况，从而完成的模式匹配，这样的结果使得算法的时间复杂度为O（m+n）

这就是所谓的KMP算法了！！！