[C++]LeetCode: 88 Factorial Trailing Zeroes (阶乘后导零)
Given an integer n, return the number of trailing zeroes in n!.
Note: Your solution should be in logarithmic time complexity.
思路:
我们要计算 N! 中有多少个后导0.
我们来找一下规律,考虑n!的质数因子。后缀0,只有可能是质因子2 * 质因子5得到。如果我们可以计算得到min{num(2), num(5)},就可以知道后导0的个数。
举例子:
n = 5! 中包含质因子(2 * 2 * 2 * 3 * 5),包含一个5和三个2. 因而后导0个数为1.
n = 11! 中包含质因子(2^8 * 3^4 * 5^2 * 7) ,包含两个5和三个2.于是后导0个数为2.
我们发现质因子中2的个数总是大于等于5的个数,所以我们只需要计算5的个数就可以了。
如何计算n!的质因子中所有5的个数? 一个简单的办法就是计算floor(n/5)(取整)。但是我们还需要考虑一件事,比如25,,125之类的5的倍数不只含有一个5. 解决办法:先对 n/5, 移除所有单个的5,然后再除以25,移除所有额外的5,以此类推。比如,25中有共有五个5,一个25,先移除单个5,floor(n/5) = 5, 再移除额外的5,floor(n/25) = 1。直到下一个数取0为止。
![]() 如何选取k
如何选取k
Attention:
1. sum需要初始化为0,否则导致未定义行为。
|
501 / 502 test cases passed.
|
Status: Wrong Answer |
|
Submitted: 31 minutes ago
|
| Input: | 0 |
| Output: | 32673 |
| Expected: | 0 |
2. 注意内存溢出的问题。 两种办法解决,不断缩小n; 或者改变变量类型。这篇文章有个内存溢出的详细解释。
i*5一直连乘时出现i = 5^14时,内存溢出(5^13 = 1220703125 < 2^31, but 5^14 = 6103515625 > 2^32)
<span style="font-size:14px;"> for(long long i = 5; n/i > 0; i *= 5)</span>
第十行代码,5^k会导致溢出。无法得到正确答案。一定要避免想当然的套用公式,首先要判断是否都在int的范围内,如果不在,考虑如何避免溢出。
Error Code:
复杂度:O(log(n))
AC Code:
<span style="font-size:14px;">class Solution {
public:
int trailingZeroes(int n) {
int sum = 0;
for(long long i = 5; n/i > 0; i *= 5)
{
sum += n/i;
}
return sum;
}
};</span>
AC Code:
<span style="font-size:14px;">class Solution {
public:
int trailingZeroes(int n) {
int sum = 0;
while(n)
{
sum += n/5;
n /= 5;
}
return sum;
}
};</span>
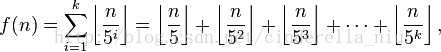
![[C++]LeetCode: 88 Factorial Trailing Zeroes (阶乘后导零)_第1张图片](http://img.e-com-net.com/image/info5/79b7a231359f409f9b8205168a3dd1a8.png)