dfs 2016.5.3

1、HDU 5676 ztr loves lucky numbers

题意：
求大于等于 n(1≤ n ≤10^18) 的各位数字只包含4和7且4和7数量相等的数字

解题思路：
初始化求出位数 <=18 的满足要求的数字
二分查找结果
注意特判10个4、10个7的解

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const LL INF = 1e18;
const int maxn = 1e5 + 10;
LL key[maxn];
int Count = 0;
char special[] = "44444444447777777777";

void dfs(LL val, int a, int b);

int main()
{
//    freopen("in.txt", "r", stdin);
    int T;
    dfs(0, 0, 0);
    sort(key, key+Count);
    scanf("%d", &T);
    while (T--) {
        LL n;
        scanf("%I64d", &n);
        int t = lower_bound(key, key+Count, n) - key;
        if (t == Count) {
            printf("%s\n", special);
        } else {
            printf("%I64d\n", key[t]);
        }
    }
    return 0;
}

void dfs(LL val, int a, int b)
{
    if (val > INF) {
        return;
    }
    if (a == b && a != 0) {
        key[Count] = val;
        ++Count;
    }
    dfs(val*10+4, a+1, b);
    dfs(val*10+7, a, b+1);
}

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const LL INF = 1e18;
const int maxn = 1e5 + 10;
LL key[maxn];
int keyval[30];
int Count = 0;
char special[] = "44444444447777777777";

int main()
{
//    freopen("in.txt", "r", stdin);
    int T;
    memset(key, 0, sizeof(key));
    for (int i=2; i<=18; i+=2) {
        for (int j=0; j<i/2; ++j) {
            keyval[j] = 4;
        }
        for (int j=i/2; j<i; ++j) {
            keyval[j] = 7;
        }
        do {
            for (int j=0; j<i; ++j) {
                key[Count] = key[Count]*10 + keyval[j];
            }
            ++Count;
        } while (next_permutation(keyval, keyval+i));
    }
    scanf("%d", &T);
    while (T--) {
        LL n;
        scanf("%I64d", &n);
        int t = lower_bound(key, key+Count, n) - key;
        if (t == Count) {
            printf("%s\n", special);
        } else {
            printf("%I64d\n", key[t]);
        }
    }
    return 0;
}

2、UVa 10004 Bicoloring

转自http://www.aichengxu.com/view/1937617

题意：
1976年“四色定理”在计算机的帮助下被证明
这个定理宣告任何一个地图都可以只用四种颜色来填充， 并且没有相邻区域的颜色是相同的

现在让你解决一个更加简单的问题
 你必须决定给定的任意相连的图能不能够用两种颜色填充
 就是说，如果给其中一个分配一种颜色， 要让所有直接相连的两个节点不能是相同的颜色
 为了让问题更简单，你可以假设：

1. 没有节点是连接向它自己的

2. 是无向图， 即如果a连接b, 那么b也是连接a的

3. 图是强连通的，就是说至少有一条路径可走向所有节点


解题思路：


取第一个点进行染色，如果发现要涂某一块时这个块已经被涂了色，并且与我们要使用的颜色不同的话，就说明这个图不能被染成BICOLORABLE的。

（1）如果没有染色，将它染色，并将它周围的点变成相反色。

（2）如果已经染色，判断是否与现在染色的点的颜色相同，相同，则退出，否则继续。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int maxn = 200 + 10;
bool Map[maxn][maxn];
int color[maxn];
bool vis[maxn];
int n;

bool dfs(int x);

int main()
{
//    freopen("in.txt", "r", stdin);
    while (scanf("%d", &n) != EOF && n != 0) {
        memset(Map, false, sizeof(Map));
        memset(vis, false, sizeof(vis));
        memset(color, 0, sizeof(color));
        int l;
        scanf("%d", &l);
        int a, b;
        for (int i=0; i<l; ++i) {
            scanf("%d%d", &a, &b);
            Map[a][b] = Map[b][a] = true;
        }
        color[0] = 1;
        vis[0] = true;
        if (dfs(0)) {
            printf("BICOLORABLE.\n");
        } else {
            printf("NOT BICOLORABLE.\n");
        }
    }
    return 0;
}

bool dfs(int x)
{
    for (int i=0; i<n; ++i) {
        if (Map[x][i]) {
            if (!vis[i]) {
                color[i] = !color[x];
                vis[i] = true;
                dfs(i);
            } else if (color[i] == color[x]) {
                return false;
            }
        }
    }
    return true;
}

3、ccf_历届题_201512-3_画图

问题描述

　　用 ASCII 字符来画图是一件有趣的事情，并形成了一门被称为 ASCII Art 的艺术。例如，下图是用 ASCII 字符画出来的 CSPRO 字样。

　　..____.____..____..____...___..
　　./.___/.___||.._.\|.._.\./._.\.
　　|.|...\___.\|.|_).|.|_).|.|.|.|
　　|.|___.___).|..__/|.._.<|.|_|.|
　　.\____|____/|_|...|_|.\_\\___/.

　　本题要求编程实现一个用 ASCII 字符来画图的程序，支持以下两种操作：
　　Ÿ 画线：给出两个端点的坐标，画一条连接这两个端点的线段。简便起见题目保证要画的每条线段都是水平或者竖直的。水平线段用字符 - 来画，竖直线段用字符 | 来画。如果一条水平线段和一条竖直线段在某个位置相交，则相交位置用字符 + 代替。
　　Ÿ 填充：给出填充的起始位置坐标和需要填充的字符，从起始位置开始，用该字符填充相邻位置，直到遇到画布边缘或已经画好的线段。注意这里的相邻位置只需要考虑上下左右 4 个方向，如下图所示，字符 @ 只和 4 个字符 * 相邻。
　　

　　.*.
　　*@*
　　.*.

输入格式

　　第1行有三个整数m, n和q。m和n分别表示画布的宽度和高度，以字符为单位。q表示画图操作的个数。
　　第2行至第q + 1行，每行是以下两种形式之一：
　　Ÿ 0 x ₁ y ₁ x ₂ y ₂：表示画线段的操作，(x ₁, y ₁)和(x ₂, y ₂)分别是线段的两端，满足要么x ₁ = x ₂ 且y ₁ ≠ y ₂，要么 y ₁ = y ₂ 且 x ₁ ≠ x ₂。
　　Ÿ 1 x y c：表示填充操作，(x, y)是起始位置，保证不会落在任何已有的线段上；c 为填充字符，是大小写字母。
　　画布的左下角是坐标为 (0, 0) 的位置，向右为x坐标增大的方向，向上为y坐标增大的方向。这q个操作按照数据给出的顺序依次执行。画布最初时所有位置都是字符 .（小数点）。

输出格式

　　输出有n行，每行m个字符，表示依次执行这q个操作后得到的画图结果。

样例输入

4 2 3
1 0 0 B
0 1 0 2 0
1 0 0 A

样例输出

AAAA
A--A

样例输入

16 13 9
0 3 1 12 1
0 12 1 12 3
0 12 3 6 3
0 6 3 6 9
0 6 9 12 9
0 12 9 12 11
0 12 11 3 11
0 3 11 3 1
1 4 2 C

样例输出

................
...+--------+...
...|CCCCCCCC|...
...|CC+-----+...
...|CC|.........
...|CC|.........
...|CC|.........
...|CC|.........
...|CC|.........
...|CC+-----+...
...|CCCCCCCC|...
...+--------+...
................

评测用例规模与约定

　　所有的评测用例满足：2 ≤ m, n ≤ 100，0 ≤ q ≤ 100，0 ≤ x < m（x表示输入数据中所有位置的x坐标），0 ≤ y < n（y表示输入数据中所有位置的y坐标）。

题意：
按题目要求画线&填充字符

解题思路：
dfs填充字符
保险起见，用vis数组进行标记，且每次填充前都要初始化vis

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 100 + 5;
char picture[maxn][maxn];
bool vis[maxn][maxn];
int m, n, q;
char c;
int dir[][4] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

void dfs(int x, int y);

int main()
{
//    freopen("in.txt", "r", stdin);

    cin>>m>>n>>q;
    for (int i=0; i<n; ++i) {
        for (int j=0; j<m; ++j) {
            picture[i][j] = '.';
        }
    }
    for (int i=0; i<q; ++i) {
        int flag;
        int x, y;
        int x1, y1, x2, y2;
        scanf("%d", &flag);
        if (flag == 1) {
            scanf("%d%d", &x, &y);
            cin>>c;
            int a = n-1 - y;
            int b = x;
            memset(vis, false, sizeof(vis));
            dfs(a, b);
        } else {
            scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
            int a1 = n-1 - y1;
            int a2 = n-1 - y2;
            int b1 = x1;
            int b2 = x2;
            if (a1 == a2) {
                if (b1 > b2) {
                    int t = b1;
                    b1 = b2;
                    b2 = t;
                }
                for (int j=b1; j<=b2; ++j) {
                    if (picture[a1][j] == '|' || picture[a1][j] == '+') {
                        picture[a1][j] = '+';
                    } else {
                        picture[a1][j] = '-';
                    }
                }
            } else {
                if (a1 > a2) {
                    int t = a1;
                    a1 = a2;
                    a2 = t;
                }
                for (int j=a1; j<=a2; ++j) {
                    if (picture[j][b1] == '-' || picture[j][b1] == '+') {
                        picture[j][b1] = '+';
                    } else {
                        picture[j][b1] = '|';
                    }
                }
            }
        }
    }
    for (int i=0; i<n; ++i) {
        for (int j=0; j<m-1; ++j) {
            cout<<picture[i][j];
        }
        cout<<picture[i][m-1]<<endl;
    }
    return 0;
}

void dfs(int x, int y)
{
    if (0<=x && x<n && 0<=y && y<m && picture[x][y] != '-' && picture[x][y] != '|' && picture[x][y] != '+' && !vis[x][y]) {
        vis[x][y] = true;
        picture[x][y] = c;
    } else {
        return;
    }
    for (int i=0; i<4; ++i) {
        dfs(x+dir[i][0], y+dir[i][1]);
    }
}

4、蓝桥杯2016省赛C语言B组3题

凑算式

       B      DEF
A + --- + ------- = 10
       C      GHI
         
    
这个算式中A~I代表0~9的数字，不同的字母代表不同的数字。

比如：
6+8/3+952/714 就是一种解法，
5+3/1+972/486 是另一种解法。

这个算式一共有多少种解法？

注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。

答案：215

解题思路：

先求出全排列，然后判断

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

const int maxn = 10 + 5;
bool vis[maxn];
int Count = 0;
int num[maxn];

void dfs(int depth);

int main()
{
    memset(vis, false, sizeof(vis));
    dfs(0);
    cout<<Count<<endl;
    return 0;
}

void dfs(int depth)
{
    if (depth == 9) {
        int GHI = num[6]*100 + num[7]*10 + num[8];
        int DEF = num[3]*100 + num[4]*10 + num[5];
        int a = num[1]*GHI + num[2]*DEF;
        int b = num[2]*GHI;
        if (a%b == 0 && a/b+num[0] == 10) {
            for (int i=0; i<9; ++i) {
                cout<<num[i]<<" ";
            }
            cout<<endl;
            ++Count;
        }
        return;
    }
    for (int i=1; i<10; ++i) {
        if (!vis[i]) {
            vis[i] = true;
            num[depth] = i;
            dfs(depth+1);
            vis[i] = false;
        }
    }
}

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;

const int maxn = 10 + 5;
int Count = 0;
int num[maxn];

int main()
{
    for (int i=0; i<9; ++i) {
        num[i] = i+1;
    }
    do {
        int GHI = num[6]*100 + num[7]*10 + num[8];
        int DEF = num[3]*100 + num[4]*10 + num[5];
        int a = num[1]*GHI + num[2]*DEF;
        int b = num[2]*GHI;
        if (a%b == 0 && a/b+num[0] == 10) {
            for (int i=0; i<9; ++i) {
                cout<<num[i]<<" ";
            }
            cout<<endl;
            ++Count;
        }
    } while (next_permutation(num, num+9));
    cout<<Count<<endl;
    return 0;
}

5、蓝桥杯2016省赛C语言B组6题

方格填数

如下的10个格子

   +--+--+--+
   |  |  |  |
+--+--+--+--+
|  |  |  |  |
+--+--+--+--+
|  |  |  |
+--+--+--+

填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

答案：1580

解题思路：

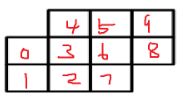
将10个格子按如下标号

全排列然后判断

代码很丑

#include <iostream>
#include <cstring>
#include <cmath>

using namespace std;

const int maxn = 10 + 5;
int num[maxn];
bool vis[maxn];
int Count = 0;

void dfs(int depth);

int main()
{
    memset(vis, false, sizeof(vis));
    dfs(0);
    cout<<Count<<endl;
    return 0;
}

void dfs(int depth)
{
    if (depth == 10) {
        if (fabs(num[0]-num[1]) != 1 && fabs(num[0]-num[2]) != 1 && fabs(num[0]-num[3]) != 1 && fabs(num[0]-num[4]) != 1) {
            if (fabs(num[1]-num[2]) != 1 && fabs(num[1]-num[3]) != 1) {
                if (fabs(num[2]-num[3]) != 1 && fabs(num[2]-num[6]) != 1 && fabs(num[2]-num[7]) != 1) {
                    if (fabs(num[3]-num[4]) != 1 && fabs(num[3]-num[5]) != 1 && fabs(num[3]-num[6]) != 1 && fabs(num[3]-num[7]) != 1) {
                        if (fabs(num[4]-num[5]) != 1 && fabs(num[4]-num[6]) != 1) {
                            if (fabs(num[5]-num[6]) != 1 && fabs(num[5]-num[8]) != 1 && fabs(num[5]-num[9]) != 1) {
                                if (fabs(num[6]-num[7]) != 1 && fabs(num[6]-num[8]) != 1 && fabs(num[6]-num[9]) != 1) {
                                    if (fabs(num[7]-num[8]) != 1) {
                                        if (fabs(num[8]-num[9]) != 1) {
//                                            for (int i=0; i<10; ++i) {
//                                                cout<<num[i]<<" ";
//                                            }
//                                            cout<<endl;
                                            ++Count;
                                        }
                                    }
                                }
                            }
                        }
                    }
                }
            }
        }

        return;
    }
    for (int i=0; i<10; ++i) {
        if (!vis[i]) {
            num[depth] = i;
            vis[i] = true;
            dfs(depth+1);
            vis[i] = false;
        }
    }
}