积性函数、线性筛、莫比乌斯反演和一堆乱七八糟的题目

某菊苣的总结，比较全面= =。

转自：http://jcvb.is-programmer.com/posts/41846.html

·积性函数
定义在正整数集上的函数（称为算术函数），若时有，则称为积性函数。
一个显然的性质：（非恒等于零的）积性函数必然满足。
定义逐点加法。
一个比较显然的性质：若均为积性函数，则也是积性函数。
积性函数的求值：，则，所以只要解决时的值即可。

例如：
恒为1的常函数，
恒等函数， 
单位函数，（这三个都是显然为积性）
欧拉函数 （只要证两个集合相等就能证明积性）
莫比乌斯函数 （由定义也是显然的）

·Dirichlet卷积
对两个算术函数，定义其Dirichlet卷积为新函数，满足。
一些性质：
交换律,
结合律,
单位元,
对逐点加法的分配律

重要性质：若均为积性函数，则也是积性函数。（展开式子即可证明）
的约数个数可以写成；约数和可以写成，由上面的性质可知这两个函数均是积性函数。

重要性质：，即。（可用二项式定理证明）
重要性质：，即。（n是质数时显然成立，再由积性得证）

·O(nlgn)预处理Dirichlet卷积
若已知的值，则可以在O(nlgn)时间内计算出。

intf[MAXN],g[MAXN],h[MAXN]={0};
voidcalc(intn)
{   
    for(inti=1;i*i<=n;i++)
        for(intj=i;i*j<=n;j++)
            if(j==i)h[i*j]+=f[i]*g[i];
            elseh[i*j]+=f[i]*g[j]+f[j]*g[i];
}

?

·线性筛O(n)预处理

intpr[MAXN],bo[MAXN]={0},tot=0;
voidsieve(intn){
    for(inti=2;i<=n;i++){
        if(!bo[i])pr[++tot]=i;
        for(intj=1;j<=tot && pr[j]*i<=n;j++){
            bo[i*pr[j]]=1;
            if(i%pr[j]==0)break;
        }
    }
}

?

可以证明每个合数只会被其最小质因子筛去，因此复杂度为线性。
如果能够充分挖掘的性质，则可以用线性筛在O(n)时间内预处理。
关键在于对下面三种情况分别进行处理：
1.是质数，求
2.是质数，，求
3.是质数，，求
第1种情况往往比较简单。如果能证明是积性函数，则容易知道第2种情况是，剩下只要解决第3种情况的递推就够了。
有时虽然不是积性函数，但也能够通过分析其性质分别解决这三种情况（后面会举一些例子）。

·一堆题目
以下均默认
1101: [POI2007]Zap
令


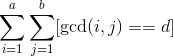
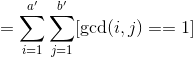
用莫比乌斯函数的性质把求和的式子换掉，

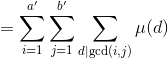
其中，更换求和指标，

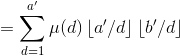
容易知道单调不上升，且最多有种不同的取值。所以按取值分成个段分别处理，一个连续段内的和可以用预处理出的莫比乌斯函数前缀和求出。

if(a>b)swap(a,b);
intnex;
ll ans=0;
for(inti=1;i<=a;i=nex+1){
    nex=min(a/(a/i),b/(b/i));
    ans+=1ll*(s[nex]-s[i-1])*(a/i)*(b/i);
}

?

整道题目预处理O(n)，每次询问O(sqrt(n))。

2005: [Noi2010]能量采集


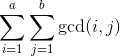
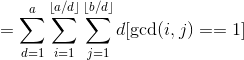
套用上题，

关键一步，作代换，把求和指标d,d'改为D,d，（容易证明这是等价的）


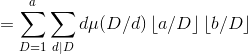
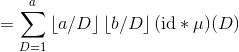
由，有，

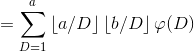
最后处理方式同上题。（不过原题只有一个询问，不分段也不要紧）

2693: jzptab


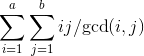
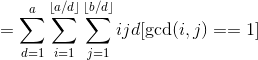
类似的方法将方括号换掉，化简为

由等差数列求和，

其中，
像上题一样代换求和指标，


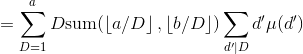
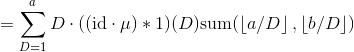
处理方式同上。
 

3309: DZY Loves Math
类似的方法化简得

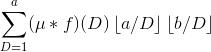
记，并不是积性函数。
观察的取值可以发现，
；
否则，当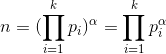时，；
否则，中存在两个质因子的次数不相同，。
上述性质容易通过展开得到证明。
这样，在线性筛的同时记录的最小质因子的次数，以及即可。