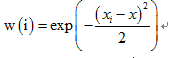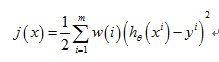非参数学习算法之局部加权回归
前面的线性回归(Linear Regression)是参数学习算法,我们需要拟合出Theta i, 如果特征值出现的太少,如只用一个theta, 可能会出现underfitting(欠拟合),如果特征值选择的过多,会几乎相连每一个点,导致函数不能反映其余数据的真实预测,这就是overfitting(过度拟合)。
比如,房屋价格的预测,它的中心思想是在对参数进行求解的过程中,每个样本对当前参数值的影响是有不一样的权重的。比如上节中我们的回归方程为(这个地方用矩阵的方法来表示Ɵ表示参数,i表示第i个样本,h为在Ɵ参数下的预测值):
我们的目标是让
最小,然后求出来Ɵ,再代入h中就可以得到回归方程了。
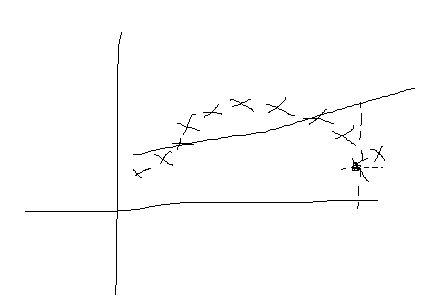
但是如果类似以下的样本,他们的对应图如下:
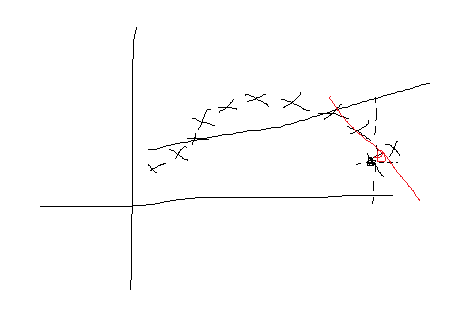
如果用之前的方法,图中线为求出的回归方程,那么在x的取值和真实差别很大,这个情况叫做欠拟合(overfitting)。那么我们怎么办呢?我们的主要思想就是只对x的附近的一些样本进行选择,根据这些样本得到x附近这些样本所推倒出来的回归方程,那么此时我们得到的回归方程就比较拟合样本数据,得到的效果图如下:
我们解的思路如下,加入一个加权因子:
重新构造新的j(x)
Exp是以e为低的指数,这个时候可以知道如果x距离样本很远的时候w(i)=0,否则为1,当我们预测一个值的时候就需要我们重新来计算当前的参数Ɵ的值,然后构造回归方程,计算当前的预测值。
这就是局部加权回归LWR!
C++实现代码如下:
#include<iostream>
using namespace std;
const int Number = 6;
const int Dimesion = 3;
const float learningRate=0.001;
const float errorThr=1; //variance threshold
const int MAX=1000; //Max times of iteration
typedef struct Data{
float vectorComponent[Dimesion];
}vectorData;
vectorData x[Number] = {
/* {1,1,4},
{1,2,5},
{1,5,1},
{1,4,2},*/
{1,1,1},
{1,1,3},
{1,1,2},
{1,2,3},
{1,2,1},
{1,2,2},
};
float y[Number]={2,10,5,13,5,8};
//lwr(局部线性回归)
float weightValue(vectorData xi,vectorData x){
float weight = 0.0;
for(int i=0;i<Dimesion;i++){
weight+=pow(xi.vectorComponent[i]-x.vectorComponent[i],2);
}
float tempWeight = exp(-(weight/(2*36)));
if(tempWeight<0.02)
tempWeight = 0.0;
return tempWeight;
}
float multiPly(vectorData x1,vectorData x2){
float temp = 0.0;
for(int i=0;i<Dimesion;i++){
temp += x1.vectorComponent[i]*x2.vectorComponent[i];
}
return temp;
}
vectorData addVectorData(vectorData x1,vectorData x2){
vectorData temp;
for(int i=0;i<Dimesion;i++)
temp.vectorComponent[i] = x1.vectorComponent[i]+x2.vectorComponent[i];
return temp;
}
vectorData minusVectorData(vectorData x1,vectorData x2){
vectorData temp;
for(int i=0;i<Dimesion;i++)
temp.vectorComponent[i] = x1.vectorComponent[i]-x2.vectorComponent[i];
return temp;
}
vectorData numberMultiVectorData(float para,vectorData x1){
vectorData temp;
for(int i=0;i<Dimesion;i++)
temp.vectorComponent[i] = x1.vectorComponent[i]*para;
return temp;
}
float costFunction(vectorData parameter[],vectorData inputData[],float inputResultData[],vectorData object){
float costValue = 0.0;
float tempValue = 0.0;
float weightedValue = 0.0;
for(int i=0;i<Number;i++){
tempValue = 0.0;
//consider all the parameters although most of them is zero
for(int j=0;j<Number;j++)
tempValue += multiPly(parameter[j],inputData[i]);
costValue += weightValue(inputData[i],object)*pow((inputResultData[i]-tempValue),2);
}
return (costValue/2*4);
}
int LocallyWeightedAgression(vectorData parameter[],vectorData inputData[],float resultData[],vectorData objectVector){
float tempValue = 0.0;
float errorCost = 0.0;
float weightedValue = 0.0;
errorCost=costFunction(parameter,inputData,resultData,objectVector);
if(errorCost<errorThr)
return 1;
for(int iteration=0;iteration<MAX;iteration++){
//stochastic
for(int i=0;i<Number;i++){
//calculate the h(x)
weightedValue = weightValue(inputData[i],objectVector);
tempValue=0.0;
for(int j=0;j<Number;j++)
tempValue+=multiPly(parameter[j],inputData[i]);
//update the parameter by stochastic(随机梯度下降)
printf("the next parameter is ");
for(int ii=0;ii<Number;ii++){
parameter[ii] = addVectorData(parameter[ii],numberMultiVectorData(weightedValue*learningRate*(resultData[i]-tempValue),inputData[i]));
if(multiPly(parameter[ii],parameter[ii])!=0){
for(int jj=0;jj<Dimesion;jj++){
printf("%f ",parameter[ii].vectorComponent[jj]);
}
}
}
printf("\n");
errorCost=costFunction(parameter,inputData,resultData,objectVector);
printf("error cost is %f\n",errorCost);
if(errorCost<errorThr)
break;
}//end stochastic one time
}//end when the iteration becomes MAX
//calculate the object vector
float resultValue = 0.0;
for(int i=0;i<Number;i++){
resultValue += weightValue(inputData[i],objectVector)*multiPly(parameter[i],objectVector);
}
printf("result value is %f \n",resultValue);
return 1;
}
int testLWA(){
vectorData objectData = {1,1.5,1.5};
vectorData localParameter[Number] = {0.0};
LocallyWeightedAgression(localParameter,x,y,objectData);
return 1;
}
int main(){
// DescendAlgorithm(parameter,x,y);
// system("pause");
//clearParameter(parameter);
//Stochastic(parameter,x,y);
//float ForTestData[] = {1,10,20};
//testData(ForTestData);
testLWA();
system("pause");
return 1;
}