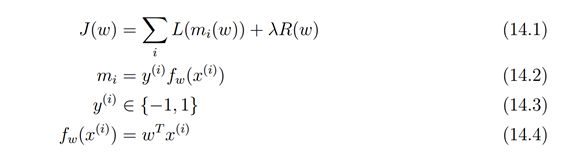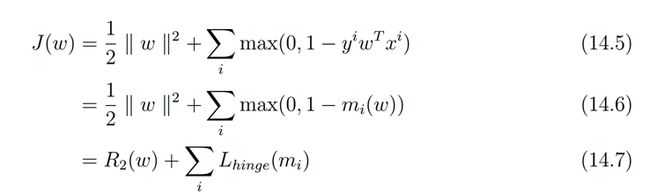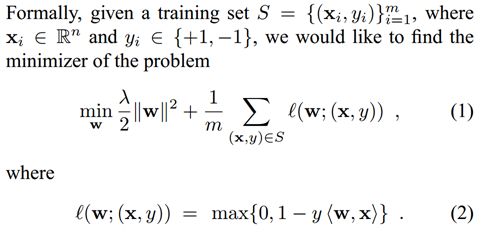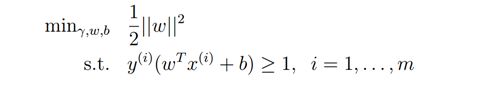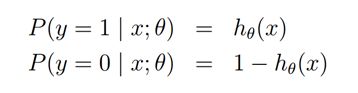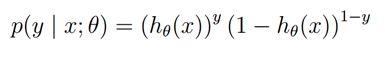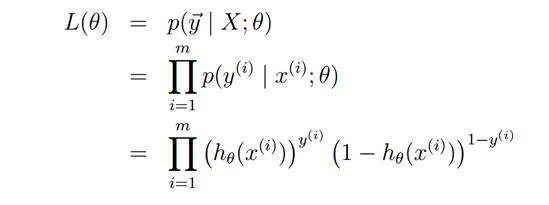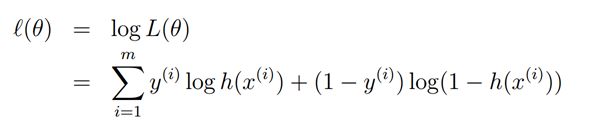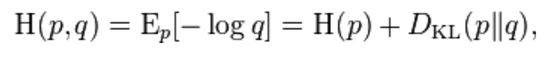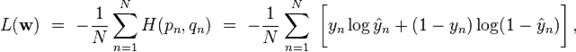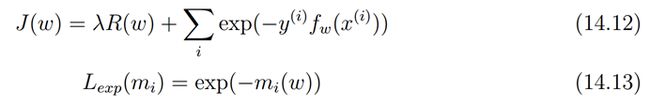损失函数
损失函数(Loss Function) -1
http://www.ics.uci.edu/~dramanan/teaching/ics273a_winter08/lectures/lecture14.pdf
1.1 Loss Term
- Gold Standard (ideal case)
- Hinge (SVM, soft margin)
- Log (logistic regression, cross entropy error)
- Squared loss (linear regression)
- Exponential loss (Boosting)
Gold Standard 又被称为0-1 loss, 记录分类错误的次数
Hinge Loss http://en.wikipedia.org/wiki/Hinge_loss
For an intended output t = ±1 and a classifier score y, the hinge loss of the prediction y is defined as
![]()
Note that y should be the "raw" output of the classifier's decision function, not the predicted class label. E.g., in linear SVMs,
![]()
It can be seen that when t and y have the same sign (meaning y predicts the right class) and
![]()
, the hinge loss
![]()
, but when they have opposite sign,
![]()
increases linearly with y (one-sided error).
来自 <http://en.wikipedia.org/wiki/Hinge_loss>
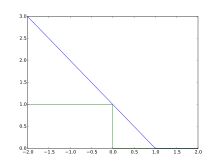
Plot of hinge loss (blue) vs. zero-one loss (misclassification, green:y < 0) for t = 1 and variable y. Note that the hinge loss penalizes predictions y < 1, corresponding to the notion of a margin in a support vector machine.
来自 <http://en.wikipedia.org/wiki/Hinge_loss>
在Pegasos: Primal Estimated sub-GrAdient SOlver for SVM论文中
这里把第一部分看成正规化部分,第二部分看成误差部分,注意对比ng关于svm的课件
不考虑规则化
考虑规则化
Log Loss
Ng的课件1,先是讲 linear regression 然后引出最小二乘误差,之后概率角度高斯分布解释最小误差。
然后讲逻辑回归,使用MLE来引出优化目标是使得所见到的训练数据出现概率最大
最大化下面的log似然函数
而这个恰恰就是最小化cross entropy!
http://en.wikipedia.org/wiki/Cross_entropy
http://www.cnblogs.com/rocketfan/p/3350450.html 信息论,交叉熵与KL divergence关系
Cross entropy can be used to define loss function in machine learning and optimization. The true probability
![]()
is the true label, and the given distribution
![]()
is the predicted value of the current model.
More specifically, let us consider logistic regression, which (in its most basic guise) deals with classifying a given set of data points into two possible classes generically labelled
![]()
and
![]()
. The logistic regression model thus predicts an output
![]()
, given an input vector
![]()
. The probability is modeled using thelogistic function
![]()
. Namely, the probability of finding the output
![]()
is given by
![]()
where the vector of weights
![]()
is learned through some appropriate algorithm such as gradient descent. Similarly, the conjugate probability of finding the output
![]()
is simply given by
![]()
The true (observed) probabilities can be expressed similarly as
![]()
and
![]()
.
Having set up our notation,
![]()
and
![]()
, we can use cross entropy to get a measure for similarity between
![]()
and
![]()
:
The typical loss function that one uses in logistic regression is computed by taking the average of all cross-entropies in the sample. For specifically, suppose we have
![]()
samples with each sample labeled by
![]()
. The loss function is then given by:
where
![]()
, with
![]()
the logistic function as before.
The logistic loss is sometimes called cross-entropy loss. It's also known as log loss (In this case, the binary label is often denoted by {-1,+1}).[1]
来自 <http://en.wikipedia.org/wiki/Cross_entropy>
因此和ng从MLE角度给出的结论是完全一致的! 差别是最外面的一个负号
也就是逻辑回归的优化目标函数是 交叉熵
修正 14.8这个公式 课件里面应该写错了一点 第一个+ 应该是-,这样对应loss 优化目标是越小越好,MLE对应越大也好。
squared loss
exponential loss
指数误差通常用在boosting中,指数误差始终> 0,但是确保越接近正确的结果误差越小,反之越大。