旋转和反射
一 概述
参见wiki(Coordinate_rotations_and_reflections)
旋转即为绕一个轴进行旋转,参见博文“三维旋转基础”,这里主要讨论反射,但是反射与旋转也存在一定的联系。
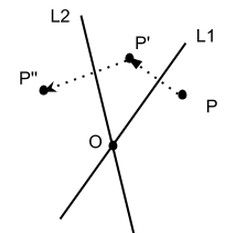
一个平面内的旋转可以通过组合一组的反射形成,如下图所示
直线L1和L2的夹角为a,角点为O,一点P经过L1反射得到P’,然后再经过L2反射得到P’’,这个时候POP’’的夹角为2a(等腰三角形被中垂线分割即可证明)。
现在定义绕原点旋转一个角度a为R(a)。同时对于一条通过原点并且与正X轴夹角为a的直线L,令它的反射为Ref(a)。二维形式下对应的矩阵分别为
反射矩阵Ref的证明参见下图
上图中,点P由直线OL进行反射得到P’,OL与x轴的夹角为θ,OP与x轴的夹角为β,OL与OP的夹角为α,可知经过反射后OP’与x轴的夹角为(θ+α)。令OP的长度为H,有:
x = Hcos(β)
y = Hsin(β)
θ = α + β
x’ = Hcos(θ+α) = Hcos(2θ-β) = Hcos(2θ)cos(β) + Hsin(2θ)sin(β) = cos(2θ)x + sin(2θ)y
y’ = Hsin(θ+α) = Hsin(2θ-β) = Hsin(2θ)cos(β) - Hcos(2θ)sin(β) = sin(2θ)x - cos(2θ)y
=> [x’ y’]’ = Ref(θ)*[x y]’ = [cos(2θ) sin(2θ);sin(2θ) - cos(2θ)]*[x y]’
=> Ref(θ)= [cos(2θ) sin(2θ);
sin(2θ) -cos(2θ)];
二 旋转矩阵和反射矩阵特性
1旋转矩阵和反射矩阵都是正交矩阵
2 旋转矩阵的行列式值为+1,反射矩阵的行列值为-1
3 旋转矩阵R(θ)的逆矩阵为R(-θ),反射矩阵的逆矩阵为其本身
4 旋转矩阵和反射矩阵可以相互转换
旋转矩阵和反射矩阵的这些特性推广到三维同样适用。