Bell数中国剩余定理

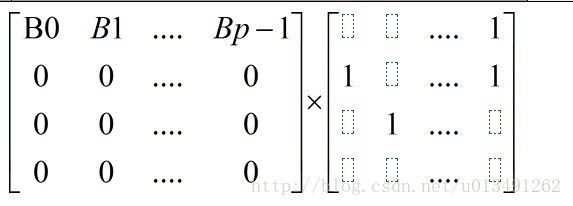
bell数的2个推论：

此题的p = 95041567太大，矩阵无法构造

而  95041567 = 31 *  37 * 41 * 43 * 47那么

x[0] =  B[n] % m[0](31)

x[1] =  B[n] % m[1](37)

x[2] =  B[n] % m[2](41)

x[3] =  B[n] % m[3](43)

x[4] =  B[n] % m[4](47)

转化成中国剩余定理模型求B[n] ,在gcd(m1,m2,m3,m4,m5)= 95041567内有解X，X即为所求（bell[n]%p）

const  int  mod  = 95041567 ;
const  int  maxn = 50 ;
LL    bell[maxn+2][maxn+2] ;
void  getbell(){ //bell[n][n] 即为第n个bell数
      bell[0][0] = 1 ; bell[1][1] = 1 ;
      for(int i = 2 ; i <= maxn ; i++){
          bell[i][1] = bell[i-1][i-1] ;
          for(int j = 2 ; j <= i ; j++)
              bell[i][j] = (bell[i][j-1] + bell[i-1][j-1]) % mod ;
      }
}

struct  Mat{
        int x[maxn][maxn] ;
};

Mat  mult(Mat A , Mat B , int md){
     Mat s ;
     for(int i = 0 ; i < md ; i++){
         for(int j = 0 ; j < md ; j++){
              s.x[i][j] = 0 ;
              for(int k = 0 ; k < md ; k++){
                  s.x[i][j] += A.x[i][k] * B.x[k][j] ;
                  s.x[i][j] %= md ;
              }
         }
     }
     return s ;
}

int  Pow(int n , int md){
     Mat s , a ;
     memset(s.x , 0 , sizeof(s.x)) ;
     memset(a.x , 0 , sizeof(a.x)) ;
     a.x[0][md-1] = a.x[1][md-1] = 1 ;
     for(int i = 0 ; i < md-1 ; i++) a.x[i+1][i] = 1 ;
     for(int i = 0 ; i < md ; i++) s.x[0][i] = bell[i][i]%md ;
     for(;n;n>>=1){
         if(n&1) s = mult(s , a , md) ;
         a = mult(a , a , md) ;
     }
     return s.x[0][0] ;
}

int  extend_gcd(int a , int b , int &x , int &y){
     if(b == 0){
          x = 1 ;
          y = 0 ;
          return a ;
     }
     else{
         int r  = extend_gcd(b , a%b , y , x) ;
         y -= x*(a/b) ;
        return r ;
     }
}

int   china(int a[] , int m[] , int n){
      int  M  = 1 ;
      for(int i = 0 ; i < n ; i++)  M *= m[i]  ;
      int ret = 0 ;
      for(int i = 0 ; i < n ; i++){
           int x , y ;
           int tm = M/m[i] ;
           extend_gcd(tm , m[i] , x , y) ;
           ret = (ret + tm*x*a[i]) % M ;
      }
      return ret ;
}

int  m[5] = {31 , 37 , 41 , 43 , 47 };
int  a[5] ;
int  main(){
     getbell() ;
     int n  , t  , i ;
     cin>>t ;
     while(t--){
           cin>>n ;
           for(i = 0 ; i < 5 ; i++)
              a[i] = Pow(n , m[i]) ;
           printf("%d\n" , china(a,m,5)) ;
     }
     return 0 ;
}