《图像局部不变性特征与描述》阅读笔记（4）-- 快速斑点检测、区域检测

快速斑点检测算法

本章主要介绍了两个算法：SIFT（SIFT特征检测）和SURF（SURF特征检测），它们分别是基于LOG和DOH的改进算法。

LOG和DOH都需要对高斯函数做二阶微分以生成卷积核，然后对图像上每个点做卷积以得到局部响应极值

为了节省卷积运算带来的时间消耗，SIFT对两个相邻高斯尺度空间的图像做差，得到一个DOG的响应图像，搜索该响应的局部极值点就是待选位置；SURF引入积分图像来近似Hessian矩阵行列式，比SIFT效率更高

此外，SIFT和SURF还将特征点的方向特征加入特征向量内（SIFT使用梯度直方图的方法统计方向，SURF使用Haar模板计算方向），使得两者具备了旋转不变性。

由于SIFT和SURF具有的高效、尺度不变、旋转不变性，一般用做图像间的特征匹配，SIFT代码中使用了BBF算法进行查找（书里将SIFT、SURF算法描述，特征描述和特征匹配分成了3章）

区域检测算法

区域检测主要是为了实现区域分割，相较于特征点，其更稳定，更易实现仿射不变性

通常区域检测分3个步骤：检测具有同类性质的区域并进行连接和标记；将检测到的非规则区域近似成一个椭圆区域（便于特征描述）；对椭圆区域进行仿射归一化处理（仿射变换为圆形）

本章重点分析了最大稳定极值区域（MSER）算法，简要介绍了基于边缘区域（EBR）、基于密度极值区域（IBR）和显著性区域（SR，使用信息熵）

MSER算法基本思想很简单：使用一个从0到255的阈值对图像二值化（类似分水岭），过程中一定范围内面积保持稳定的区域即为所求。这个算法的重点是实现技巧。

椭圆区域仿射归一化这一步，我的理解是：无论是哪个角度的图像，得到的椭圆区域，都将其仿射并缩放成同一尺寸的圆形，这样在一定程度上实现了仿射不变性

下面是椭圆到圆的仿射实现，对于一个标准椭圆，如果令（相当于y方向做缩放），则变为圆，注意标准椭圆的长短轴是分别平行于XY轴的，所以对一般椭圆，还需做旋转

void main()
{
	cv::Mat img = cv::imread("../file/spots.jpg");
	
	//截取椭圆区域
	cv::Mat ellipImg;
	float sita = 30;
	int a = img.cols/2;
	int b = img.rows/4;
	getEllipse(img, ellipImg, a/2, b/2, sita);

	//旋转pi-sita
	cv::Mat rotateImg(img.size(), img.type(), cv::Scalar::all(0));
	rotate_(ellipImg, rotateImg, sita);

	//调整b轴
	cv::Mat affImg(img.size(), img.type(), cv::Scalar::all(0));
	affine_(rotateImg, affImg, a, b);

	//反向旋转pi-sita
	cv::Mat affineImg(img.size(), img.type(), cv::Scalar::all(0));
	rotate_(affImg, affineImg, 180-sita);

	cv::namedWindow("source", 0);
	cv::namedWindow("step1", 0);
	cv::namedWindow("step2", 0);
	cv::namedWindow("step3", 0);
	cv::namedWindow("dst", 0);
	cv::imshow("source", img);
	cv::imshow("step1", ellipImg);
	cv::imshow("step2", rotateImg);
	cv::imshow("step3", affImg);
	cv::imshow("dst", affineImg);

	cv::waitKey(0);
}

void getEllipse(cv::Mat src, cv::Mat& dst, int a, int b, float sita)
{
	cv::Point center(src.cols/2, src.rows/2);
	dst = cv::Mat(src.size(), src.type(), cv::Scalar::all(0));

	for (int i = 0; i < dst.rows; i++)
	{
		uchar* ptr = dst.ptr<uchar>(i);
		for (int j = 0; j < dst.cols; j++)
		{
			cv::Point tmp(j-center.x, i-center.y);
			cv::Point realP;
			// 因为图像坐标系转成的坐标系左下角才是正（对应笛卡尔左上角的第一象限）
			// 所以正负关系与笛卡尔下的相反，下同
			realP.x = tmp.x*cos(sita*PI / 180) - tmp.y*sin(sita*PI / 180);
			realP.y = tmp.y*cos(sita*PI / 180) + tmp.x*sin(sita*PI / 180);

			float value = float(realP.x*realP.x) / (a*a) + float(realP.y*realP.y) / (b*b);
			if (value <= 1)
			{
				ptr[3 * j] = src.at<cv::Vec3b>(i, j)[0];
				ptr[3 * j + 1] = src.at<cv::Vec3b>(i, j)[1];
				ptr[3 * j + 2] = src.at<cv::Vec3b>(i, j)[2];
			}
		}
	}
}


void rotate_(cv::Mat src, cv::Mat& dst, float sita)
{
	for (int i = 0; i < dst.rows; i++)
	{
		uchar* ptr = dst.ptr<uchar>(i);
		for (int j = 0; j < dst.cols; j++)
		{
			cv::Point tmp(j - dst.cols / 2, i - dst.rows/2);
			cv::Point srcP;
			srcP.x = int(tmp.x*sin(sita*PI / 180) - tmp.y*cos(sita*PI / 180) + 0.5);
			srcP.y = int(tmp.y*sin(sita*PI / 180) + tmp.x*cos(sita*PI / 180) + 0.5);

			srcP.x += src.cols / 2;
			srcP.y += src.rows / 2;

			if ((srcP.x >= 0 && srcP.x < src.cols) &&
				(srcP.y >= 0 && srcP.y < src.rows))
			{
				ptr[3 * j] = src.at<cv::Vec3b>(srcP)[0];
				ptr[3 * j + 1] = src.at<cv::Vec3b>(srcP)[1];
				ptr[3 * j + 2] = src.at<cv::Vec3b>(srcP)[2];
			}
		}
	}
}

void affine_(cv::Mat src, cv::Mat& dst, int a, int b)
{
	float rate = b / float(a);
	for (int i = 0; i < dst.rows; i++)
	{
		uchar* ptr = dst.ptr<uchar>(i);
		for (int j = 0; j < dst.cols; j++)
		{
			cv::Point srcP;
			srcP.y = i;
			srcP.x = int(rate*(j-src.cols/2) + 0.5);
			srcP.x += src.cols / 2;

			if ((srcP.x >= 0 && srcP.x < src.cols) &&
				(srcP.y >= 0 && srcP.y < src.rows))
			{
				ptr[3 * j] = src.at<cv::Vec3b>(srcP)[0];
				ptr[3 * j + 1] = src.at<cv::Vec3b>(srcP)[1];
				ptr[3 * j + 2] = src.at<cv::Vec3b>(srcP)[2];
			}
		}
	}
}

特征描述方法

重点介绍了SIFT和SURF的特征组织方法（详细分析见相应算法文章），实验表明SURF比SIFT的特征描述更好，一是前者维数为4*4*4=64，小于后者（一般为4*4*8=128），匹配更快速；二是前者是基于模板求和得到的梯度方向，而后者是基于单个像素统计的梯度，抗噪能力更好。

PCA-SIFT特征描述法：通过对同类图像的学习（PCA主成分分析），得到一个投影矩阵，对原始的SIFT特征进行维数约减

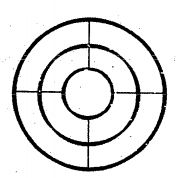
GLOH特征描述法：将SIFT中4*4的子块改成一组同心圆，将其按方向划分成不同的区块（图3-1），统计每个区块的梯度方向，然后使用类似PCA-SIFT的方法，对特征进行维数约减

图3-1. GLOH

旋转图像（Spin-image）特征描述法：将区域描述为二维直方图，横轴为该点距中心的距离，纵轴为该点的亮度（这样就具有了旋转不变性）

图3-2. 旋转图像