EM算法学习笔记
声明:
1)该博文是多位博主以及书籍作者所无私奉献的论文资料整理的。具体引用的资料请看参考文献。具体的版本声明也参考原文献
2)本文仅供学术交流,非商用。所以每一部分具体的参考资料并没有详细对应,更有些部分本来就是直接从其他博客复制过来的。如果某部分不小心侵犯了大家的利益,还望海涵,并联系老衲删除或修改,直到相关人士满意为止。
3)本人才疏学浅,整理总结的时候难免出错,还望各位前辈不吝指正,谢谢。
4)阅读本文需要机器学习、概率统计算法等等基础 。
5)本人手上有word版的和pdf版的,有必要的话可以上传到csdn供各位下载
一.EM算法解决的问题
要了解EM算法,就先了解这个算法是干啥的,十大算法之一头衔怎么来的。当然这个头衔是专家们投票得来,只是这个投票跟现在的选秀节目投票不一样,EM是凭借硬实力胜出的,有铁杆粉丝称之为“神的算法”。
EM算法之前,先要了解极大似然估计方法,这个在转发的博文《从最大似然到EM算法浅解》里面有讲解了。
极大似然估计能解决很大一部分的参数估计问题了,类似逻辑回归,RBM等等,都看到了它的影子,确实及其常用。
然而极大似然估计也是有极限的,起码基本的要求是:样本都是来自同一个分布的,然后就帮忙估计这个分布的参数(如高斯分布,就估计均值和方差,这两个量都是参数)。
当遇到下面的情况:样本来自多个分布的。简单地说就是样本的一部分来自分布A,又有一部分来自分布B,……,这样就有多个分布了(当然,资深的数学爱好者还会认为这么说不对,他们认为应该是样本里面的每一个个体都是一部分属于分布A,一部分属于分布B,……,也就是说样本的每个个体都是按概率属于多个分布的)。然后还有一个制约就是:每个样本都不知道来自哪个分布的。
要估计这么多个分布的参数,极大似然估计就不行了,这一团糟的场面它处理不了。
EM算法就是专门解决这种疑难杂症的,方法也快刀斩乱麻:直接每个个体胡乱指一个分布,然后就分别去估计每个分布的参数;估好后再根据情况把每个个体调节一下,该属哪个分布就分配到哪个去,然后再估计每个分布的参数(江湖上也是这么来的,一开始小弟们都随便认个老大,结成各个帮派,然后帮派之间又选取新老大,选完后不爽的小弟就跳槽到他爽的老大那去;跳完后各个帮派又开始选老大,小弟又洗牌,最后稳定下来的,就成了江湖)。
为了方便描述,举个例子,暂且认为江湖上只有两个门派,高富帅派和矮穷丑派。有一天武林要举行炫富大赛,两大门派都派了4名高手去参加比赛。比赛过程不多说了,倒是这次比赛亮出来的财富亮瞎了某武林高手的狗眼,他很生气,就派人抓了这8个人,当然为了比赛,这8位高手都穿得西装革履的,外表看不出来哪个帮派的。这位高手很想知道哪些人是高富帅派的,哪些是矮穷丑派的,而且还想知道这两派的实力,所以要知道这两派的财富的均值和方差,还要知道两派分别来了多少人。
这个时候,这位高手就只能用EM算法了。
二.EM算法数学描述
EM算法分两步,E步和M步,总的流程如下:
E步:对于每一个样本,计算这个样本属于各个分布的概率(指派每个样本个体的归属,也就是求出来每个样本属于各个分布的概率,从而确定 这个分布的概率密度函数,离散型的就是求到了概率)M步:最大化似然Q函数,求得参数θ(这个θ包括了样本所属的每个分布的里面的所有参数,如100个高斯分布,就求出了100个均值和100个方差),Q函数定义如下
其中的 表示样本xi属于各个分布的概率密度函数,注意z这个东西,它可能有多种取值,也可能是个向量,甚至是连续的。是离散的情况的时候,只需要求每一种情况的概率,如果z^((i) )是连续值的时候, 要用概率密度函数或者概率函数表示, 表示参数θ的上一轮的迭代值或者初始值。
总之在E步就需要得到每个样本所属的类别,这个类别指定可能只需要用一些简单的量,那就把这个量求出来就可以了。E步求这个“所属类别”的目的是为了写出Q函数的形式来,而且这个形式不带着隐变量,也就是z这个东西。这样是为了保证能在求解问题的过程中不需要考虑隐变量,从而能想求解极大似然那样,得到一个闭式解或者迭代的解法。
M步中的那个Q函数(名字千百种,这里就叫这种吧),是每个样本个体的对数似然函数 在条件概率分布 下的期望(注意求期望其实是求积分),然后再对每个样本的值都累加起来,得到了总的最大化的目标。
三.EM算法数学基础
来些数学上的描述,把符号交代一下吧。问题可以描述成:给定观测到的样本集合x1,x2,x3…,xn,目标是找到每一个样本个体隐含的类别z(注意z可能是由一个向量表示的),使得p(x,z)最大。
解法还是极大似然那一套,目标函数定义为
要求的参数原来是θ,但是无端端多了个z,就不好办了,闭式的迭代式都搞不出来了。
搞不出来也得想办法搞,观察样本个体xi的对数似然,再看联合概率,先不管参数θ,用贝叶斯定理展开
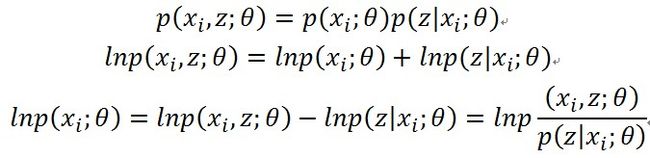
取样本xi对隐变量z的分布(也就是样本xi属于各个类别的概率)的总和,得到下面的全概率
把上面的东西加上来

这里可以看到,每个样本的对数似然函数都分成了两部分,分开讨论吧,令
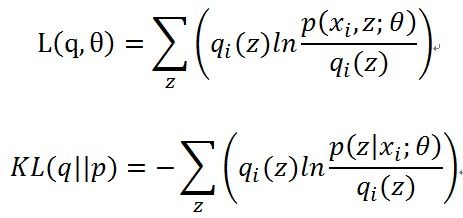
那么可以用下面的示意图来表达对数似然函数值的分解

每个样本个体都可以这样划分的,所以对数似然函数变成了下面的样子
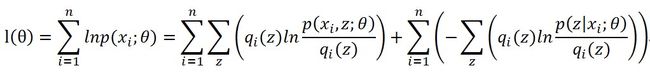
前半部分就是Q函数,后半部分就是每个样本p分布和q分布的KL距离。
再看看E步做的事情,
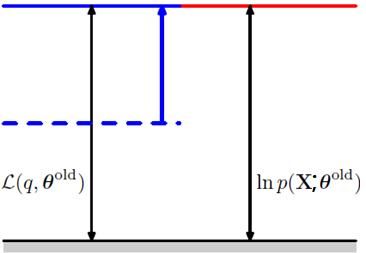
再来看看M步做的事情,求Q函数的最大化,获取了新的θ值θ^new。这样导致的结果就是Q函数的值提升了,而且p和q分布又不一致了,KL距离再度变大了,从而整体的对数似然函数的值也提升了。就像下面的图表示的一样。
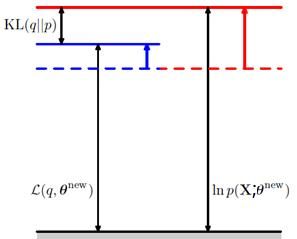
这样两步不断地做,对数似然函数就不断地被提升,直到逐渐收敛到一个对数似然函数序列的稳定点。如下面的示意图。

当然不能保证收敛到极大值点。初值选取对这个也有影响的,这个就不多讨论了。
四.EM算法实际例子
现在开始看(一)的那个例子,假设这八个人的财富值分别是0.8,0.9,1.0,1.3,9.8,9.9,10.0,10.3。一开始不知道怎么搞,当然在之前就认为他们各自的财富属于一个正态分布的,就乱假设:
假设矮穷丑派是1类,高富帅派是2类,用k指定,
再假设矮穷丑派财富均值 ,标准差 ,也就是
再假设高富帅派财富均值 ,标准差 ,也就是
当然 ,需要的话可以把这个写成一个矩阵,这里就不纠结符号的写法了
再假设矮穷丑派的人数比例是 ,高富帅派的人数比例是 。
一、开始E步,计算每个样本归属,首先计算每个样本属于每个类别的概率值,根据
来计算,得到一个样本归属的矩阵A
0.0167 0.0001
0.0342 0.0001
0.0659 0.0001
0.3229 0.0001
0.0001 0.1111
0.0001 0.0067
0.0001 0.0038
0.0001 0.0007
又因为
0.9999 0.0001
0.9999 0.0001
0.9999 0.0001
0.9999 0.0001
0.0009 0.9991
0.0147 0.9852
0.0256 0.9743
0.1250 0.8750
二、开始M步
最大化Q函数
其中i=1,2……8,k=1,2。
且
把上面的值代进去,然后解这个优化问题,得到参数。
从这组参数看来,已经相当靠谱了,再迭代一轮,基本到最优解了。
搞几轮就能知道,矮穷丑派的财富均值是1.0,方差是0.1870,有4个人;高富帅派的财富均值是10.0,方差是0.1870,也有4个人。
还有就是注意那个Q函数的问题,其实分母是没啥用的,常量,可以考虑去掉再做最优化。
致谢
互联网上JerryLead,zouxy09等多位博主以及LeoZhang的指导。
李航的书,以及PMLR的作者。
参考文献
[1] http://blog.csdn.net/zouxy09/article/details/8537620 @ zouxy09的博客
[2] http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html@JerryLead的博客
[3]《统计学习方法》 李航
from: http://blog.csdn.net/mytestmy/article/details/38778147