什么是bootstrap?
Bootstrap又称自展法,是用小样本估计总体值的一种非参数方法,在进化和生态学研究中应用十分广泛。例如进化树分化节点的自展支持率等。
Bootstrap的思想,是生成一系列bootstrap伪样本,每个样本是初始数据有放回抽样。通过对伪样本的计算,获得统计量的分布。例如,要进行1000次bootstrap,求平均值的置信区间,可以对每个伪样本计算平均值。这样就获得了1000个平均值。对着1000个平均值的分位数进行计算, 即可获得置信区间。已经证明,在初始样本足够大的情况下,bootstrap抽样能够无偏得接近总体的分布。
下面是一个实例:
例如,假设有一批产品,随机抽出30个,使用寿命(天数)如下,试用bootstrap的方法估计这批产品寿命95%的置信区间。
dat <- c(119,120,131,209,210,337,332,287,146,1
29,232,169,208,253,142,105,419,179,
324,287,115,132,308,356,286,221,204,
105,45,245)
Bootstrap的思想,是生成一系列bootstrap伪样本,每个样本是初始数据有放回抽样。通过对伪样本的计算,获得统计量的分布。例如,要进行1000次bootstrap,求平均值的置信区间,可以对每个伪样本计算平均值。这样就获得了1000个平均值。对着1000个平均值的分位数进行计算, 即可获得置信区间。已经证明,在初始样本足够大的情况下,bootstrap抽样能够无偏得接近总体的分布。
下面是一个实例:
例如,假设有一批产品,随机抽出30个,使用寿命(天数)如下,试用bootstrap的方法估计这批产品寿命95%的置信区间。
dat <- c(119,120,131,209,210,337,332,287,146,1
29,232,169,208,253,142,105,419,179,
324,287,115,132,308,356,286,221,204,
105,45,245)
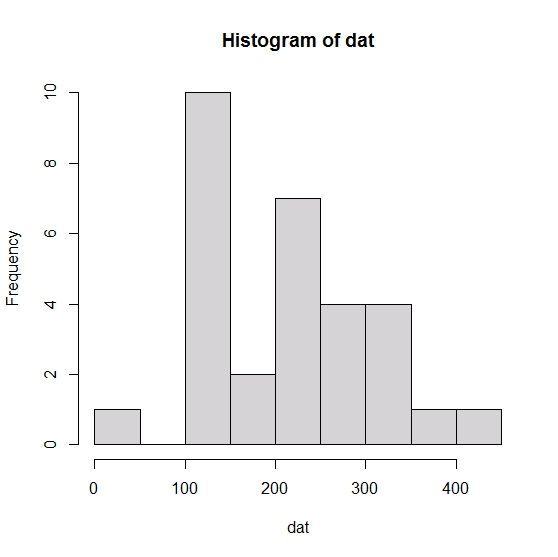
### 查看原始数据的频数直方图
hist(dat, col="gray")
#生成一个存储器
boot.sample <-list()
## 循环1000次,有放回的抽样,每次生成的
## 新样本存储在boot.sample中
for(i in1:1000){
boot.sample[[i]]<-sample(dat,size =30, replace=TRUE)
}
## 求每个样本的mean,结果为1000个bootstrap样本的mean
boot.mean <-unlist(lapply(boot.sample, mean))
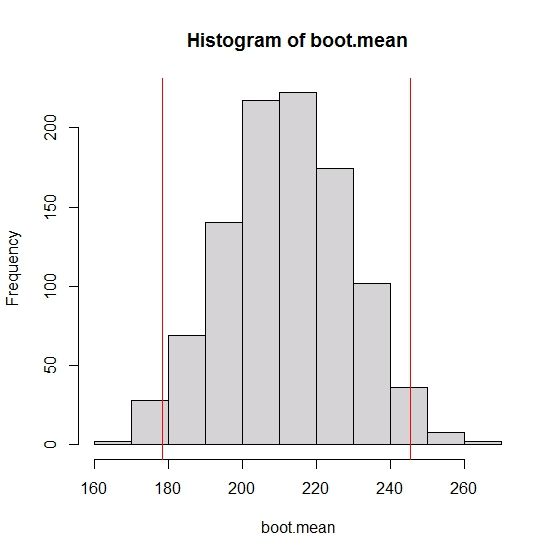
## 频数直方图
hist(boot.mean, col="gray")
## 求95%的置信区间
CI95 <-quantile(boot.mean, probs =c(0.025, 0.975))
## 在频数直方图上加置信区间
abline(v = CI95, col="red")
本文引用地址: http://blog.sciencenet.cn/blog-255662-523462.html