[COGS1862]种树 解题报告

【问题描述】

A城市有一个巨大的圆形广场，为了绿化环境和净化空气，市政府决定沿圆形广场外圈种一圈树。园林部门得到指令后，初步规划出n个种树的位置，顺时针编号1到n。并且每个位置都有一个美观度Ai，如果在这里种树就可以得到这Ai的美观度。但由于A城市土壤肥力欠佳，两棵树决不能种在相邻的位置（i号位置和i+1号位置叫相邻位置。值得注意的是1号和n号也算相邻位置！）。
最终市政府给园林部门提供了m棵树苗并要求全部种上，请你帮忙设计种树方案使得美观度总和最大。如果无法将m棵树苗全部种上，给出无解信息。

【输入格式】

输入的第一行包含两个正整数n、m。
第二行n个整数Ai。

【输出格式】

输出一个整数，表示最佳植树方案可以得到的美观度。如果无解输出“Error!”，不包含引号。

【样例输入】

7 3
1 2 3 4 5 6 7

【样例输出】

15

【样例输入】

7 4
1 2 3 4 5 6 7

【样例输出】

Error!

【数据规模和约定】

对于全部数据：m<=n；
-1000<=Ai<=1000
N的大小对于不同数据有所不同：

分析：

一、部分分算法：

很容易想到的是N^2的DP。。考试的时候，我就写了这个。

但是。。有一些地方没有注意到，下次要注意：①数组一定要开大一点点，防止越界；判断越界的条件一定要写在&&的前面，防止越界。

二、满分算法：sto——cstdio大神。

这个题解正确性的证明来自类似数规的思想，因为比较困难。。所以，被打上了贪心的标签。

我们可以简单地考虑第一次选择的情况。

若此时最大的数为，则在最优解中，易知若不选，则与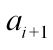必同时被选，因为若与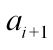没有同时被选，则显然可以将被选的那个换成得到至少不更差的解。

然后。。。

然后我就放弃了，但是题解没有放弃。

题解非常巧妙地使用了一个等效替换的方式，拜托了被选数不能相邻的限制。

当题解选了一个最大值后，题解在原数列中删去那三个数，并同时加入一个数，并用其替代掉原数列中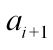，，三个数，维护其在原数列中相对其他数的位置（双向链表）。

这样的话，就相当于在剩下n-2个数中再选m-1个数；并且我们可以发现ak对数量的贡献依然为1，正如一个普通的数一样。既然其满足如此多地性质，我们不禁想要假设在第二步操作中其依然满足此性质。

综上，一个完整的贪心策略（辅以堆+双向链表）便脱颖而出了。

这种神题往往是能给我们一些启示的：

②复杂的问题往往是由简单的问题变形或组合而来的，在面对复杂的问题时从简单的问题出发往往可以获取一些灵感。

③当面对题目不知所措时，发掘题目中的一些性质往往是解题的黄金之匙：诸如可逆性、对称性、等效性等等，尤其是一些奇怪的性质，绝对是破题的关键；而思考的方向也往往围绕着最值、特殊点等等进行，盲目探索只会消磨时间。

#include<iostream>
using namespace std;
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define size 200001
int heap[size],heapsize=1,point[size],a[size],l[size],r[size];
inline void down(int x){
	int now=x,next=x<<1;
	//cout<<"D:"<<heap[x]<<endl;
	while(next<heapsize){
		if(next+1<heapsize&&a[heap[next+1]]>a[heap[next]])++next;
		if(a[heap[now]]>a[heap[next]]){/*
			for(int i=1;i<heapsize;++i)
				printf("%d(%d) ",heap[i],a[heap[i]]);
			cout<<endl;*/
			return;
		}
		//cout<<"(D)"<<heap[now]<<":"<<now<<"->"<<next<<endl;
		swap(heap[now],heap[next]);
		swap(point[heap[now]],point[heap[next]]);
		now=next,next<<=1;
	}
}
inline void up(int x){
	int now=x,next=x>>1;
	//cout<<"U:"<<heap[x]<<endl;
	while(next){
		if(a[heap[next]]>a[heap[now]]){/*
			for(int i=1;i<heapsize;++i)
				printf("%d(%d) ",heap[i],a[heap[i]]);
			cout<<endl;*/
			return;
		}
		//cout<<"(U)"<<heap[now]<<":"<<now<<"->"<<next<<endl;
		swap(heap[now],heap[next]);
		swap(point[heap[next]],point[heap[now]]);
		now=next,next>>=1;
	}
}
char * ptr=(char *)malloc(10000000);
inline void in(int &x){
	bool flag=0;
	while(*ptr<'0'||*ptr>'9')
		if(*ptr++=='-')
			flag=1;
	x=0;
	while(*ptr>47&&*ptr<58)x=x*10+*ptr++-'0';
	if(flag)x=-x;
}
int main(){
	freopen("nt2011_tree.in","r",stdin);
	freopen("nt2011_tree.out","w",stdout);
	int N,M,i,ans=0;
	fread(ptr,1,10000000,stdin);
	in(N),in(M);
	if(N<M<<1){
		printf("Error!");
		return 0;
	}
	for(i=0;i<N;++i)in(a[i]);
	for(i=N-2;i;--i)
		l[i]=i-1,r[i]=i+1;
	l[0]=N-1,r[0]=1,l[N-1]=N-2,r[N-1]=0;
	for(i=0;i<N;++i){
		point[i]=heapsize;
		heap[heapsize]=i;
		up(heapsize++);
		down(point[i]);
	}/*
	printf("\n-----------0----------\n");
	for(int i=1;i<heapsize;++i)
		printf("%d(%d) ",heap[i],a[heap[i]]);*/
	while(M--){
		ans+=a[heap[1]];
		//cout<<heap[1]<<":"<<l[heap[1]]<<" "<<r[heap[1]]<<endl;
		
		heap[point[l[heap[1]]]]=heap[--heapsize];
		point[heap[heapsize]]=point[l[heap[1]]];
		up(point[heap[heapsize]]);
		down(point[heap[heapsize]]);
		
		heap[point[r[heap[1]]]]=heap[--heapsize];
		point[heap[heapsize]]=point[r[heap[1]]];
		up(point[heap[heapsize]]);
		down(point[heap[heapsize]]);
		
		a[heap[1]]=a[l[heap[1]]]+a[r[heap[1]]]-a[heap[1]];
		l[heap[1]]=l[l[heap[1]]];
		r[heap[1]]=r[r[heap[1]]];
		l[r[heap[1]]]=heap[1];
		r[l[heap[1]]]=heap[1];
		down(1);
		
		/*printf("-----------%d----------\n",M);
		for(int i=1;i<heapsize;++i)
			printf("%d(%d) ",heap[i],a[heap[i]]);
		cout<<endl;*/
	}
	printf("%d",ans);
}