POJ 2411 Mondriaan's Dream（铺装问题） 状态DP

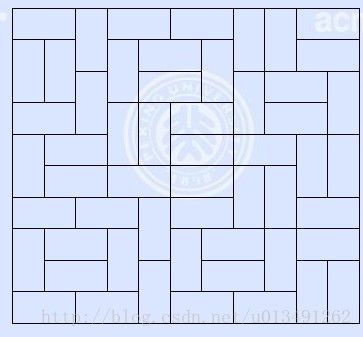
题意：  水平、垂直1*2 去铺满n*m不同种数。

这个题很多报告，希望我这个说明对朋友你有帮助。

对于每一个格子用0 ，1 。 其中

1  ：  垂直上半部分

0：   case1 :   横放

         case2： 垂直下半部分

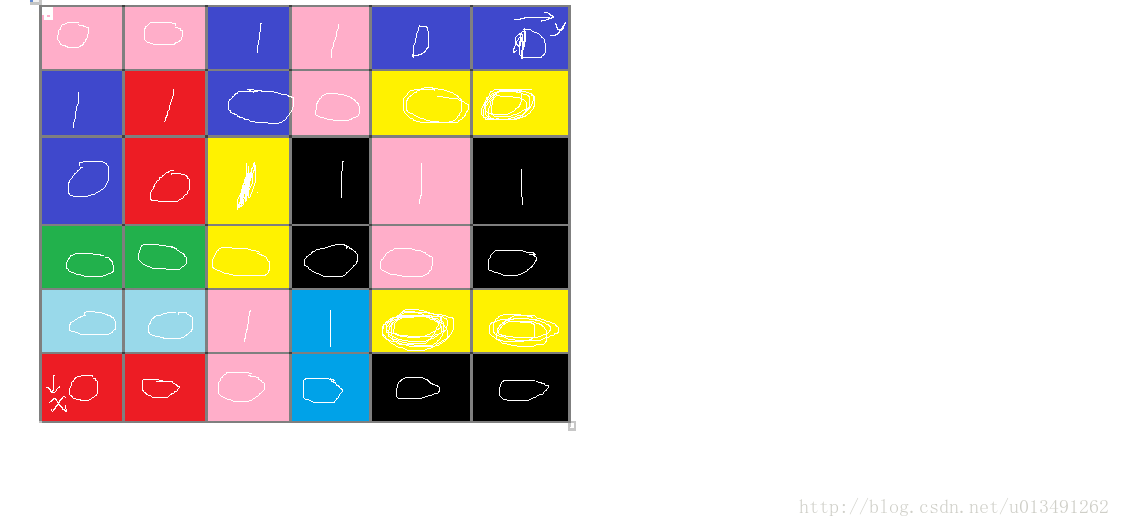
对上图的标号为：

（画的有点猥琐啊，哈哈）

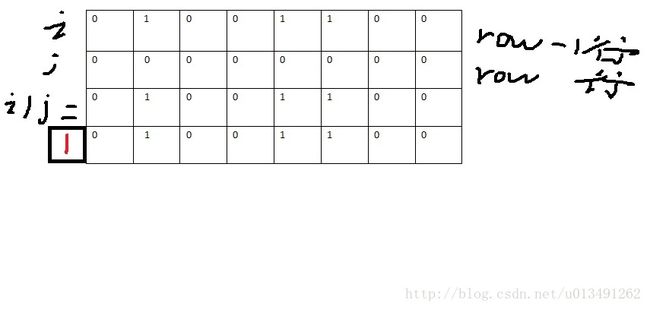
可见当我们标号到最后一行为止，且最后一行数全为0时，为一种可行解。

dp方程就比较简单了。如果row行状态i,与row-1行状态j不排斥   ，有：

        dp[row][i] += dp[row-1][j] ;

怎样判断状态i,j可以共存呢？状态i,j 对于的二级制，必须同时满足2点：

1：相同位不能同时为1 。 1表示垂直的上半部分， 同时为1的时候，覆盖矛盾。

2（i , j）.相同位3种情况（0,1）（1,0） （0,0） ，其中（0,1）（1,0） 都可行。但是（0,0）特别注意。

  连续（0,0）的个数必须为偶数，因为（0，0）是横放，而横放必须是1*2的小方格。

也就是说i|j连续0的个数必须为偶数，为了取出i|j连续0的个数。

想到了lowbit(x) = x & (-x)函数，取出x二进制末尾第一个不为0的位置所对应的十进制数。

防止例如i|j =（00001000100）这种情况，在i|j的最高位补上1变为（100001000100）。

typedef long long LL ;
LL dp[12][1<<11] ;
int n , m ;
int lowbit(int x){
    return x & (-x) ;
}

int zero(int x){
    int c = lowbit(x) ;
    int sum = 0 ;
    while(c){
        sum++ ;
        c>>=1 ;
    }
    return sum - 1 ;
}

int ok(int x){
    x += (1<<m) ;
    while(x){
        int z = zero(x) ;
        if(z&1)
            return 0 ;
        x>>=(1+z) ;
    }
    return 1 ;
}


LL DP(){
   memset(dp , 0 , sizeof(dp)) ;
   dp[0][0] = 1 ;
   int i , j , row ;
   for(row = 1 ; row <= n ; row++){
      for(i = 0 ; i < (1<<m) ; i++){
          for(j = 0 ; j < (1<<m) ; j++){
              if(!(i&j) && ok(i|j))
                  dp[row][i] += dp[row-1][j] ;
          }
      }
   }
   return dp[n][0] ;
}

int main(){
    while(cin>>n>>m){
        if(n == 0 && m ==0)
           break ;
        if(n < m)
            swap(n , m) ;
        cout<<DP()<<endl ;
    }
    return 0 ;
}