整数拆分的两种解法（已完成）

 

整数拆分的两种解法（已完成）

4.1 集合的分划和第二类Stirling数
定义1  (集合的划分)
设A 是有限集.A 的一族子集{Ai}称为是集A 的一个划分
,如果满足:
(1)每个子集Ai 都非空;
(2)这些子集两两不交;
(3)它们的并为A.
每个Ai称为划分的一个块,有k个块的划分称为k- 划分.
定义2 (第二类Stirling 数)
一个n元集的所有k- 划分的个数,用S(n,m) 表示,称为第二类Stirling 数.

注:将一个n元集划分成m块,就相当于将n个有区别的球放到m个相同的盒子中使得无一空盒.
例:求3元集和4元集的所有划分数.
由S(n,m) 的定义易知:
S(n,1)=1;
S(n,n)=1;
S(n,k)=0 (k ＞n)
S(n,k)对任何正整数n和k都有定义.

4.2第二类Stirling数的性质
定理1
第二类Stirling数S(n,k)满足递推关系S(n+1,k)=S(n,k-1)+kS(n,k).
证明:易验证k=n+1成立;k＞n+1 时也成立.当1≤k≤n时取n+1 元集A 的某一元素a, 将A 的k- 划分分成两类:一类是a 作为单独一块的,一类是a 不是单独一块的.第一类的划分数为S(n,k-1), 第二类的划分分成两步来实现,一步为将A 中除了元素a 划分成k块,第二步将a 放入某一块中.由乘法原理得第二类的划分数为kS(n,k).最后由加法原理,定理得证.

将第二类Stirling数列成表,它与杨辉三角类似.
定理2
第二类Stirling数S(n,k)满足下列性质
(1) S(n,2)=2的n-1次方-1;
(2) S(n,n-1)=C(n,2).
证明1:可由定理1递推得到.
证明2:由组合意义:
(1)S(n,2)是n元集A={a1,a2,…,an}的2-划分数.先取a1,则对于a2,…,an各有两种选择,或者和a1在同一块,或者不在同一块.但不能都和a1在同一块.
(2)S(n,n-1)是n元集A={a1,a2,…,an}的n-1-划分数.这样的划分必定一块有2个元素,其余的块都只有1个元素.只要确定了2个元素的块就确定了这个划分.

定理3
第二类Stirling数S(n,k)满足S(n+1,k)=C(n,k-1)S(k-1,k-1)+C(n,k)S(k,k-1)+…+C(n,n)S(n,k-1).
证明：S(n+1,k)是集合A={a1,a2,..,an，an+1}的k分划数。对于A的一个k分划，设包含an+1的那块是B,则其余的k-1块构成了A\B的一个k-1分划。反过来，给定A的一个含an+1 的子集B，若A\B含有至少k-1个元素，则A\B的一个k-1分划加上B就构成A的一个k分划。令C=A\B，易看出结论成立。

4. 3 正整数的有序分拆
定义3  (有序分拆)正整数n的一个k分拆把n表示成k个正整数的和n=n1+n2+…+nk(k ≥1)若分拆不仅与ni的值有关,也与它们的顺序有关.则称为有序k分拆.
例如4=2+1+1
=1+2+1
=1+1+2
是4的所有3个有序3分拆.注:正整数n的一个有序k-分拆,就相当于将n个无区别的球放到k个不同的盒
子中使得无一空盒.

定理4
正整数n的有序k分拆的个数为C(n-1,k-1).证明: 正整数n的有序k分拆n=n1+n2+…+nk等价于在n个竖杠的n-1个空隙中插入k-1个杠子.这样的方法数为C(n-1,k-1).
4. 4 正整数的无序分拆
定义4 (无序分拆)
正整数n的一个k分拆把n表示成k个正整数的和n=n1+n2+…+nk(k≥1)若分拆只与ni的值有关,与它们的顺序无关.则称为无序k分拆.我们用B(n,k)表示n的无序k分拆的个数,用B(n)表示n的所有分拆的个数.

注:正整数n的一个无序k- 分拆,就相当于将n个无区别的球放到k个相同的盒子中使得无一空盒.
例如: 4=4
=3+1=2+2
=2+1+1
=1+1+1+1
显然有
(1)B(n,k)=0 (k＞n);
(2)B(n,1)=1;
(3)B(n,n)=1;
(4)B(n)=B(n,1)+B(n,2)+…+B(n,n).

定理5
正整数n的无序k分拆的个数B(n,k)满足递推关系B(n+k,k)=B(n,1)+B(n,2)+…+B(n,k).
证明:我们考虑所有n的分成至多k个分部的分拆,这样的分拆总数为B(n,1)+B(n,2)+…+B(n,k).n的每个分成至多k个分部的分拆可表示为n=n1+n2+…+nm+0+…+0,这里n1≥n2≥…≥nm1≤m≤k
这个和式包含k项.它与n+k的下述k分拆一一对应.n+k=(n1+1)+(n2+1)+…+(nm +1)+1+…+1,这里n1≥n2≥…≥nm1≤m≤k

分类： 算法 2012-09-30 17:04  263人阅读  评论(0)  收藏  举报

目录(?)[-]

1. 题目：给定一个整数n，输出这个整数拆分的可能总数
   1. 分析一
   2. 分析二
2. 题目二：给定一个整数n，输出这个整数拆分的可能形式（即输出全部情况）

前几天在算法书上看到一个整数拆分的题目，觉得挺有意思，记录如下：

 

题目：给定一个整数n，输出这个整数拆分的可能总数

例如：n==6有

6

5+1

4+2    4+1+1

3+3    3+2+1     3+1+1+1

2+2+2     2+2+1+1        2+1+1+1+1

1+1+1+1+1+1

共11种分解方法，所以输出应该为11。

分析一

拆分按照因子从大到小排列，每一次拆分都可视为问题规模的减少，所以可以使用递归解决。

设q(n,m)为整数n使用不大于m的整数进行拆分的所有情况总数，因此有

1）当n==m时

可以分为两种情况，一个是使用n本身，只有一种情况。二个是使用不大于n-1的整数进行拆分。

所以此时q(n,m)=1+q(n,n-1)；

2）当n<m时

使用比n大的数进行拆分没有意义，所以此时q(n,m)=q(n,n)

3）当n>m时

这时候有两种情况，一个是使用m对n进行拆分，一个是使用小于m的数对n进行拆分

对于第一个，使用m对n进行拆分，所以拆分出来的情况最大的数是m，剩下的所有数加起来为n-m，问题变成使用不大于m的整数对n-m进行拆分，所以此时为q(n-m,m)

对于第二个，使用小于m的数对n进行拆分，表示为q(n,m-1)

4）当n==1或者m==1时 只有一种情况，返回1。注意，这里可能会漏掉m==1的情况，实际上这种情况是存在的。

所以可以使用递归函数编程如下：

 #include <stdio.h>
 #include <algorithm>
 using namespace std;

 int q(int n,int m){
     if(n==1||m==1){
         return 1;
     }
     if(n<m)  return q(n,n);
     if(n==m){
         return q(n,m-1)+1;
     }
     if(n>m)
         return q(n,m-1)+q(n-m,m);
 }

 void main(){
     int n;
     while(scanf("%d",&n)!=EOF){
         printf("%d\n",q(n,n));
     }
 }

分析二

使用母函数法

整数分解用母函数可以这样理解，分别用任意个1，2，3，4，……，n可以加起来可以表示成n的种数。又因为当使用整数m对n进行分解时，所使用的次数不能多于n/m次，所以可以写下母函数如下：

G(x)＝(1+x^1+x^2+……+x^n)*(1+x^2+x^4+……+x^((n/2)*2))*……

          ＊(1+x^m+x^(2*m)+x^(3*m)+……+x^((n/m)*m))*……*(1+x^n)

在程序中使用set数组表示每一轮乘法后得到系数，c数组表示到现在为止乘法得到的系数总和。最后算出结果后x^n对应的系数则为可分解的可能数。代码如下：

 #include<stdio.h>
 const int num=1000;
 int set[num];
 int c[num];
 void init(){
     for(int i=0; i<num; i++){
         c[i]=1;
         set[i]=0;
     }
 }

 int main(){
     int n;
     int sum;
     init();
     while(scanf("%d",&n)!=EOF){
         sum=0;
         init();
         for(int i=2; i<=n; i++){
             for(int j=0; j<=n; j+=i){
                 for(int k=0; j+k<=n; k++){
                         set[k+j]+=c[k];
                 }
             }
             for(int x=0; x<=n; x++){
                 c[x]=set[x];
                 set[x]=0;
             }
         }
         printf("%d\n",c[n]);
     }
     return 0;
 }

题目二：给定一个整数n，输出这个整数拆分的可能形式（即输出全部情况）

使用递归情况（输出实在麻烦。。弄了很久(>﹏<)）

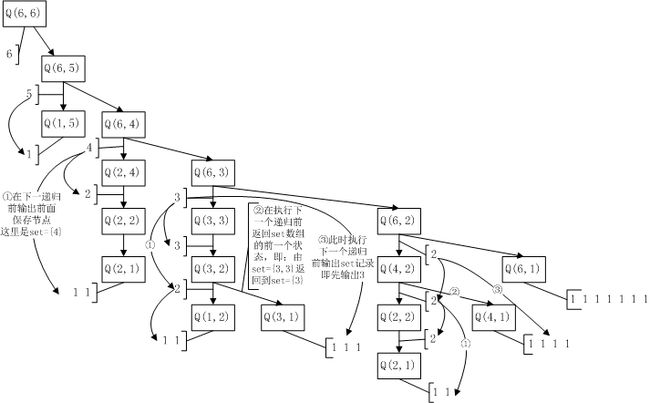
整个输出类似于一颗树，以分解6为例，过程如下图

 代码如下：

 #include <stdio.h>

 //使用一个数组记录在递归过程中产生的前面需要重复输出的值
 int set[100];
 //用于在递归过程中判断是否递归到最深处，输出回车
 int k;

 //此函数表示使用不大于m的整数对n进行拆分的情况，i用于表示set数组已经存在的记录数长度
 void q(int n,int m,int i){
     if(n==k&&n!=m){
         //此时递归栈已经退回到某一分支的最上层，输出回车
         //并重置计数器i为0
         printf("\n");
         i=0;
     }
     if(n==1){
         //当n为1，意味者着只能表示1
         printf("1 ");
         return;
     }
     else if(m==1){
         //当m为1，意味着要输出n个m相加
         for(int i=0; i<n-1; i++)
             printf("1+");
         printf("1 ");
         return;
     }
     if(n<m) {
         q(n,n,i);
     }
     if(n==m){
         //当n等于m时，到达本次递归求和的一个叶子，此时需要输出多一个空格，表示下一次输出为另一个叶子
         printf("%d ",n);
         //在递归输出另一个叶子之前，将之前记录的在叶子之上的数一并输出，如上图示过程1
         for(int j=0; j<i; j++)
             printf("%d+",set[j]);
         q(n,m-1,i);

     }
     if(n>m){
         //如果n大于m，使用m作为分解，则要首先输出m+的形式
         printf("%d+",m);
         //记录下作为树干节点m的值并使i自增
         set[i++]=m;
         //递归输出m+以后的分解
         q(n-m,m,i);
         //递归完毕后需要将数组记录后退一个，回到上一个节点，如上图示过程2
         i--;
         //执行另一个分支，在下一次递归之前输出记录的数据，如上图示过程3
         for(int j=0; j<i; j++)
             printf("%d+",set[j]);
         //递归输出另一分支情况
         q(n,m-1,i);
     }


 }

 void main(){
     int n;
     while(scanf("%d",&n)!=EOF){
         if(n<=0){
             printf("Please input a positive interger.\n\n");
             continue;
         }
         k=n;
         q(n,n,0);
         printf("\n\n");
     }
 }