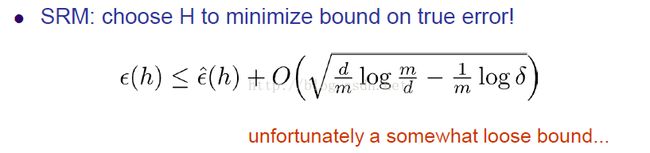机器学习---过拟合和模型选择
以下内容主要在讲:我们怎样选取一个好的模型,判断模型好坏的指标或者选取策略是神马
到目前为止我觉得下边说了这么多
分割线前边有用的就一句——我们选取模型的时候需要考虑两个条件,1、error(基于约束条件)尽可能小,2、d(模型维数)尽可能小
分割线后边还是比较有用的
以下使用到的图片来自上海交大杨旸老师的课件,网址如下:http://bcmi.sjtu.edu.cn/~yangyang/ml/
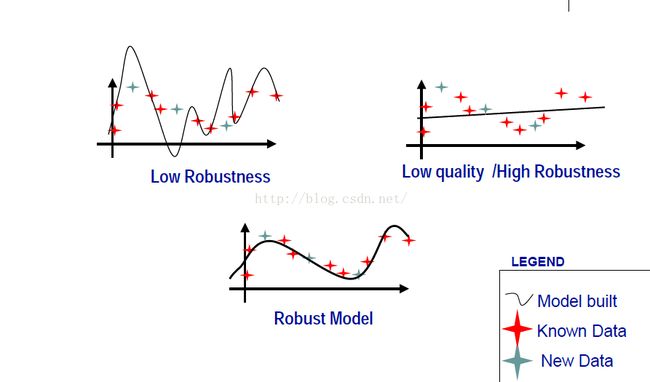
下图中红色为训练点集,灰色为测试点集。
我们可以看出来第三个是拟合最好的,但是实际中的数据很可能是多维空间的,不能画图直观看出来,这时候我们就需要用到以下策略来帮助我们“看”出模型好还是不好。
1、模型的一致性,即test和train的准确率如何达到比较近的水平
2、模型收敛速度,即当样本容量增大的时候我们应该怎样提升泛化能力(好像模型不变的情况下,样本容量增大,本身泛化能力就会提升额。。)
3、泛化能力控制,即我们拥有的数据数量是有限的,这时我们应该怎样提升泛化能力——于是我们用到了SRM策略
一致性
第一幅图中test error和train error的距离 比第二幅图中的距离近,这就说明第一个模型比较好,也就是拥有一致性。
原因就是。。。我尽量描述,咳咳。
假如你使用你拥有的部分数据训练得到的模型的维数和理想中的模型的维数不一样,那么无论你怎么训练,训练出来的模型相比于维数更加合理的模型总是有更多的误差,很多条件考虑不到,无论你包含了多少数据,test都不能完全get到train想要表达的意思,所以他们之间差的就蛮多的,并且不能通过增加训练数据量来弥补这一缺陷。
为什么test error 和 train error 两条曲线不会相交呢?因为数据有噪声。
那么什么情况下我们才能得到一致性的模型呢?
一个模型是一致的,当且仅当这个函数h来自一个有限维数d的函数家族H。意思就是这个模型是有限维的才OK,比如多项式。
test和train的错误差的本质是什么呢?
我们只需要知道结论就OK啦~这个差取决于一个由模型维数d和训练样本大小m的比值,d/m。K.S.这位前辈已经证过了。
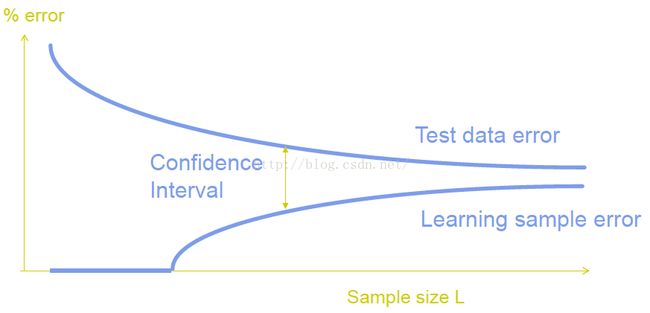
上边提到的那个差,我们起名叫做:confidence interval(置信区间)
注意这个图中的横坐标是L!下边我们还会看到一个图中也提到了置信区间,但是置信区间是越来越大的,因为下图的横坐标不一样啊~
这边可以这样理解一下,你的模型维数固定了,那么采样数量越多,置信区间就越小嘛,也可以不太严谨地(因为先忽略一下learning sample error)说你的模型就越好。
下面我们来聊一下SRM:
为神马我们会想要用SRM,因为实际中不会有人想用上边那个图来减小误差的。。。因为你既然有更多的数据,为什么不用!为什么还要用变量的数量作为横坐标,直接选一个大的值就OK了啊~
SRM就是讲,数据量固定了,选取一个好的函数的方法
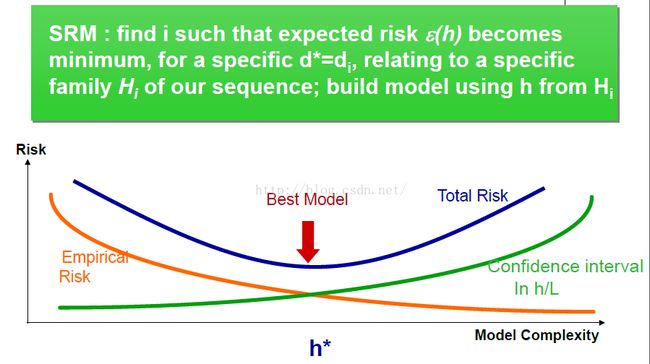
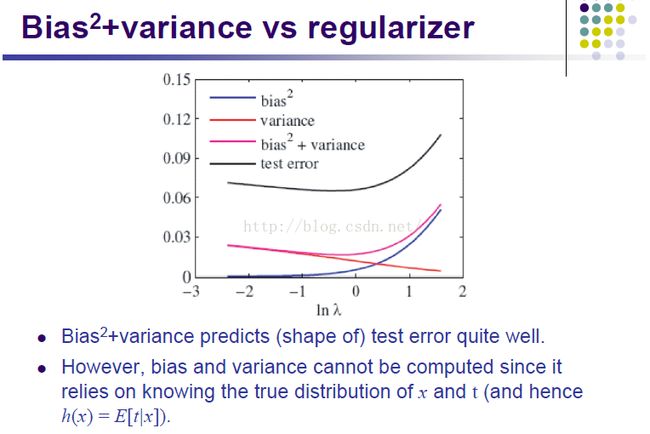
我们需要做的是,让实验中的错误和置信区间的和最小。
这个图中的置信区间是增加的,因为和上边那个图对比来看,我们的横坐标变了,可以这样想,如果你的样本数量确定了,那么你的模型维数越高,你预测的就越不准确。
橙色的线就是:如果你的样本数量确定了,你的模型维数越高,那么对于训练数据来说,拟合也就越好(当然之后可能产生过拟合问题),所以错误也就越小。
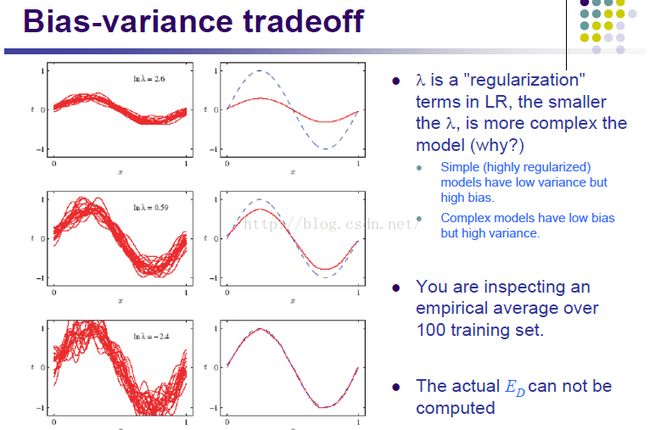
PPT里最开始还有这样一个图:
Variance:类比为上上图的置信区间
Bias:类比为上上图的实验风险
Y是真实值,f(x)是理想状态拟合的函数,f*(x)是训练得到的模型
我们想要的那个最优的模型,就是中间那个鞍点(上边那条线的最低点)
这个公式左边是true error, 上边也有一个true error,然而两个式子左边计算的方法还不一样~这是因为:
上边的等式是在计算true error,然而下边的式子是在计算true error的上界。具体过程没有列出来,可能看着比较费劲,但是我觉得并不需要理解....反正不影响我们使用模型。
另外这个式子,在使用的时候要记得控制其中一边变量不变,否则是不能用的。
因为我们想让前边那个e(h)小于后边那两项,但是如果d增大了,那么后边大O那一项也会跟着增大,这样算出来的不等号前边那项其实也在增加的,所以我们需要控制d不能太大。
即:我们需要两个条件,1、错误尽可能小,2、d也要尽可能小
上边这个式子其实也都不会用到,有用的就是上一行加粗的两个条件~
总觉得自己被骗看了很多没有神马卵用的内容,它们存在的意义应该就是为了让你坚信这个结论是对的~
可能纯描述公式不太容易理解,我们可以看个例子——线性模型
首先不管我们的约束条件是什么,一看到这个式子,我们的第一反应就是要控制维数!X的维数,也就是W的维数,为神马要用它的膜呢?如果可以设计一个更好的方式,那也不错~
无论是规范化还是SVM我们都可以看到式子中有控制 ||W|| 的地方~so,它们是好的~
关于规范化,我们再多说一点~
再解释一遍:1、式子前面arg.....那一项就是约束条件,2、后边 入theta 就是约束d(维数)用的,所以它符合SRM
右边两个图就是说我们采用不同的规范化方法,模型边界是不一样的,所以最终得到的最优解也是有差别的~
L1就是|x|+|y|这种距离
L2就是欧式距离(根号x方加y方)
如果规范化程度越高,模型就有更低的普适性,有更高的偏见
LR就是线性回归
——就是对自身的适应性好,对其他测试集适应性不好?不太对啊。。
上图是讲如果你的模型拟合的test error 和之前图中的true error可以类比的。但是test集中的数据毕竟不是所有的数据,所以test error和true error还是略有不同
我是分割线——————————————————————————————————————————————————————————————
上边写了那么多没神马用的我也不是很懂的内容,下边终于又有一点点有用的知识了——感天动地!
我们在选择模型的时候不知道取多少次方才是好的,不知道局部权重应该如何选择,不知道隐层状态如何选择~
就是说我们想要实验某一个函数族里边到底参数怎么取才会有更好的效果~
以下介绍的几个方法可以用于处理上边的参数问题(也算是解决过拟合问题):
1、交叉验证
2、正则化——这个理解为给模型增加一些我们设定的规则(通常是先验的已知的参数或者模型)
3、特征选择
4、信息标准
5、贝叶斯模型平均
1、交叉验证(cross validation)
我们来举个例子:
(1)我们有200个标记好的数据,我们分为10组,每组20个数据。每次取出其中1组(也就是20个)作为测试数据,另9组(180个)作为训练数据,来训练我们选择的模型,这称为一次训练&测试。之后我们选择另一个作为测试数据,其他9个作为训练数据,再测....。一共进行K次,每次都选不同的组作为测试数据。最终训练K(这个我们自己定)次得到的准确率的平均值即为所求(下边会用到)。
(2)比如我们选择的是线性模型,但是并不知道几次方才是最好的~
(3)那么我们就对最高次数分别为1,2,3,...,n次方的线性模型(一共n个)都用(1)中介绍的流程算一遍准确率的平均值,如果 i 次方的模型对应的平均准确率最高,那么 i 次方的线性模型就是最好的。
交叉验证的过程中需要我们确定的参数是:alpha(每组数据个数占总数据的比例),训练次数K(换多少次测试数据)
通常K = 10,alpha = 0.1
当数据集和模型没神马关系的时候,也就是用已经选取的K和alpha做交叉验证检测不出来哪个好的时候,我们就要减小alpha,增加K
K需要大一些,这样才能让模型的普适性足够小(方便你找出好的模型),但是这也会增加时间开销,所以选取的时候还是要权衡一下的。
小的alpha通常会有比较小的偏见,理论上LOOCV(leave one out cross validation,就是每次只从数据中选出一个作测试,其他为训练数据),但是这样普适性就太强二楼
大的alpha会减小普适性,但是会出现数据使用不足(就是训练数据不够)的情况,增加偏见。
很重要的一点在进行交叉验证的时候不能用你最终用作测试的数据。
不然你在做交叉验证的时候就已经学了好多测试例子,之后再用测试例子来测试就显得不是那么客观了。
为神马叫做交叉验证,因为一直都是那些数据,但是轮流作为训练和测试数据,算是一种交叉吧。。。就起了这个名(我猜的)
2、正则化——即:在原函数中增加规则项
中心思想就是根据我们之前的经验给模型画个圈,只能在这个范围活动。因为你觉得有些一看就不对的数据~模型往其他方向走就是浪费时间嘛,或者你本来就知道应该是什么样子的,那就直接传授一下经验,省得走弯路嘛。
看最后一个例子——贝叶斯:P(D)就是先验的。(分子的那两个参数。。忘了是不是了。。)总觉得哪里理解不太对。。。
贴个我能看懂的吧。。线性模型后边都习惯加一个 (入|| theta ||),这就是规则项,咋选(入)呢,用前边讲的交叉验证就OK
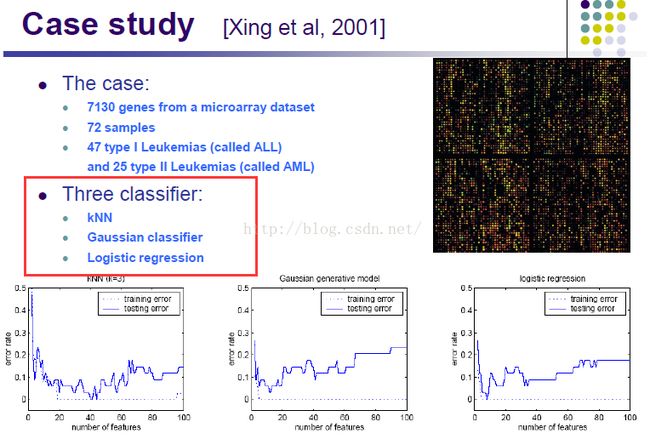
3、特征选择
在我们训练的时候很多特征都是没有用的,那么我们得到了那么多特征,怎么找到没用的特征并去掉他们呢?
选取对分类最有用的那些特征
上边的公式左边是,特征集 X 中的第 i 个特征对其标签的贡献率。右边是算概率的公式吧,为什么是这么算,我也不知道。。xi 特征标签为0或者1,y 取0或者1。总之就是 y 取0还是1,和 xi 取值为0还是1 的相关性有多大。
但是我们有n个特征,我们就有2^n 个待选的特征集,因为每个特征都有在还是不在这个集合中的可能。这样算起来开销就太大了。so, 我们还有其他方法来帮你选!
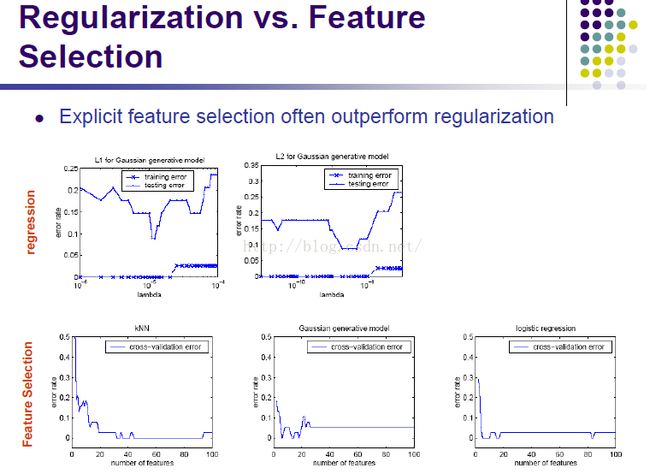
特征选择可以用上边红框中的三个方法
特征选择比正则化好
4、信息标准(Information criterion)
我们不仅可以让J包含损失信息(之前是把这个函数叫做损失函数吧。。),也可以反映出它包含了多少信息。
没懂0.0
5、贝叶斯模型平均
用于选模型吧~
就是这个data已经确定的情况下我们使用M好还是不好的概率~~某种程度上的准确率