回溯法入门

        

     回溯法：(Backtracking)

        回溯法（backtracking）是暴力搜寻法中的一种,具有“通用解题法”之称. 用该方法可以系统的去搜索一个问题的所有解或者任一解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先策略，从根节点出发搜索解空间树，总是先判断该节点是否肯定不包含问题的解. 如果肯定不包含,则跳过对以该节点为根的子树的系统搜索，逐层向其祖先节点回溯. 否则的话则进入该子树，继续按深度优先的策略进行搜索. 回溯法在用来求问题的所有解的时候,要回溯到根，且根节点的所有子树都以被搜索完毕才结束。

        回溯法尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：1)找到一个可能存在的答案   2)   在尝试了所有可能的分步方法后宣告该问题没有答案。(From 维基百科)

        在最坏的情况下，回溯法会导致一次复杂度为指数时间的计算。

     回溯法的算法框架：

        1.问题的解空间

        应用回溯法解决问题的时候,首先应该明确定义问题的解空间.问题的解空间至少包含问题的一个最优解.然后需要将问题的解空间用特定数据结构组织起来，使得回溯法可以很方便的能够搜索整个解空间。通常我们将解空间组织称树或者图的形式.

        Example：

        例如上文中得0/1背包问题，n个可选择的物品，每个物品可以选择放入或者不放入，那么这个问题的解空间就是长度为n的0-1 向量组成。(0代表该物品未被选中,1代表物品被选中了).则当n=3的时候,0/1背包的解空间可以用一颗完全二叉树表示.

        每一层的一个0/1代表1个物品做出的选择.因为有3个物品，每2个节点可以代表一层，所以树的高度为4.

        2.回溯法的基本思想：

        

        首先确定解空间组织结构，然后从根节点开始扫描，采用深度优先搜索的方式扫描整个树。开始节点成为一个活节点，同时也成为当前的拓展节点.在当前扩展节点处,搜索向纵深方向移到一个新节点.这个新节点然后成为一个新的活节点.并成为当前扩展节点.如果由于某种条件,当前拓展节点不能向纵深方向移动,则当前拓展节点成为死节点.此时就需要回溯到最近的一个活节点处，并且使这个活节点重新成为当前的扩展节点.然后继续搜寻.回溯法就是以这种递归的方式在解空间搜索，直至找到解或者解空间没有活节点存在.

        Example：分析上面n=3的0/1背包问题。设w[]=[16,15,15]  p = [45,25,25] ,c = 30        w为物品重量,p为物品价值  c为包的重量.   假设包的剩余重量为left,包的价值为value ,初始情况下 value=0,left = 30.

        从根节点开始出发搜索其解空间，开始的时候根是唯一的活节点.也是当前的扩展节点. 然后我们可以沿纵深方向移到B或者C节点，走B代表第一个物品背包，走C代表第一个物品不放入背包.假设我们走B节点,此时节点A和B都是活节点,B为当前扩展节点.left= 30-w[1] = 14, value = value + p[1] = 45,  在节点B处我们继续移至节点D或者E处,由于移动到D需要重量为15,我们当前为14,So 移动到节点D导致一个不可行解. D为死节点,移动到E不需要背包重量,可行.移动到E,E为活节点且为当前的扩展节点,同理分析移至J会导致不可行解,J为死节点,移动到K,left=14,value = 45,因为K为叶子节点.代表我们得到一个可行解.  解的值为45,由于K不能在往下走了,所以K为死节点.返回到E,在E也没有可扩展的节点, E也变为死节点.

        继续返回到B,则节点B也变为死节点.从而到A,A的纵深方向C是可以的.可以按照刚才的方法搜寻.可以搜索整个空间树。搜索结束得到的最好解就是0/1背包问题的解.

        Example2:旅行售票员问题.

        某售货员要到若干城市去推销商品，一直各城市之间的路程，他要选定一条从驻地出发，经过每个城市一遍，最后回到住地的路线，使总的路程最短. 

        路线是一个带权图.图中各边的费用(权)为整数.图的一条周游路线是包括每个定点在内的一条回路.周游路线的费用是这条路线上的所有费用之和.回溯法解决这个问题.首先构造问题的解空间.可以构造成一颗树.如下图：

        假设有4个点,构造右边的解空间.先选定一个节点,然后构造解空间树.路线有(n-1)!条.

        搜索的情况类似Example1,只是这个问题不需剪枝函数.需要挨个遍历所有的情况.

        剪枝函数：

         

        在使用回溯法搜索解空间树时,通常采用两种策略来避免无效的搜索(提高回溯法的搜索效率) ,这两种函数统称为剪枝函数.

        1)  约束函数在扩展节点处剪去不能满足约束的子树(Example1中 不能满足包重量限制的那些子树,即导致不可行解的子树)

        2) 用界限函数剪去不能得到最优解的子树.(Example2中如果根节点到扩展节点的费用已经超过当前找到最好的周游路线费用,则可以判定以该节点为根的子树中不包含最优解,剪去).

        我们可以得出回溯法解题步骤： 1) 定义问题解空间  .  2)确定易于搜索的解空间结构  3)深度优先搜索树解空间,并且运用剪枝函数避免无效搜索.

        3.回溯法的解法框架

    

        1)递归回溯  回溯法是采用深度优先搜索搜索解空间，因此一般可以用递归函数来实现回溯法.

  

        CodeFrame:

void Bcktrack(int t) //参数t表示当前递归深度
{
    if(t>n)Output(x); //遍历到解，则将解输出或其他处理  n用来控制递归深度即解空间树的高度
    else
    {
        //f(n,t)和g(n,t)表示当前节点（扩展节点）处未搜索过的子树的起始编号和中指编号
        for(int i=f(n,t);i<=g(n,t);i++)    
        {
            x[t]=h(i);    //h(i)表示当前节点（扩展节点）处x[i]的第i个可选值
            if(Constarint(t)&&Bound(t)) //剪枝函数：约束函数，限界函数
                Bcktrack(t+1);
        }
    }
}

        可以用这个方法对旅行售票员问题进行求解,练练手

        旅行售货员问题：

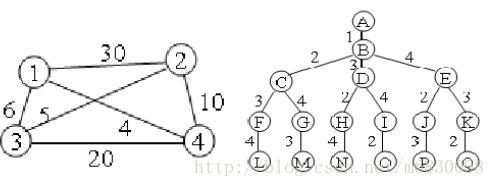
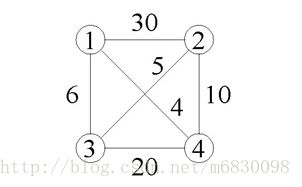
        设G=（V，E）是一个带权图。图中各边的权代表各城市间旅行费用。图的一条周游路线是包括V中的每个顶点在内的一条回路。周游路线的费用是这条路线上所有边的费用之和。旅行售货员问题就是要在图G中找出费用最小的周游路线。如下图所示是一个4顶点无向带权图。顶点序列1，2，4，3，l；1，3，2，4，1和1，4，3，2，1是该图中3条不同的周游路线。

        

        旅行售货员问题的解空间可以组织成一棵树，从树的根结点到任一叶结点的路径定义了图G的一条周游路线。如图5-3所示是当n=4时解空间的示例。其中从根结点A到叶结点L的路径上边的标号组成一条周游路线l，2，3，4，1。从根结点到叶结点O的路径表示周游路线1,3,4,2,1。图G的每一条周游路线都恰好对应于解空间树中一条从根结点到叶结点的路径。因此，解空间树中叶结点个数为（n-1）！。

        


        对于图5-2中的图G，使用回溯法寻找最小费用周游路线时，从解空间树的根结点A出发，搜索至B，C，F，L。在叶结点L处记录找到的周游路线1,2,3,4,1，该周游路线的费用为59。从叶结点L返回至最近活结点F处。由于F处已没有可扩展结点，算法又返回到结点C处。结点C成为新扩展结点，由新扩展结点，算法再移至结点G后又移至结点M，得到周游路线1，2，4，3，1，其费用为66。这个费用不比已有周游路线1，2，3，4，l的费用更小，因此，舍弃该结点。算法又依次返回至结点G，C，B。从结点B，算法继续搜索至结点D，H，N。在叶结点N处，相应的周游路线1，3，2，4，1的费用为25，它是当前找到的最好的一条周游路线。从结点N算法返回至结点H，D，然后从结点D开始继续向纵深搜索至结点O。依此方式算法继续遍历整个解空间，最终得到最小费用周游路线1，3，2，4，1。

        代码：

#include <iostream>

using namespace std;

#define N 100
#define NOEDGE -1
#define NOEDGELENGTH 99999
int map[ N ][ N ];      //记录城市之间路径信息，没有则为-1
int p[ N ];             //代表城市节点信息
int bp[ N ];            //记录最佳路径的那个信息
int bestL = NOEDGELENGTH;  //记录最佳路径的长度

int cuL = 0;            //记录当前路径的长度
int n;

void Swap( int &x, int &y ){
    int temp;
    temp = x;
    x = y;
    y = temp;
}
void initMap( int n ){
    int i, j ;
    for( i = 1; i <= n; i++ ){
        p[ i ] = i;
        for( j =1; j <= n; j++ ){
            cin >> map[ i ][ j ];
        }
    }
}
void backTrack( int i ){
    if( i == n ){
        if( map[ p[ n - 1 ]][ p [ n ] ] != NOEDGE && map[ p[ n ]][ 1 ] != NOEDGE
           && ( bestL == NOEDGELENGTH || cuL + map[ p[ n - 1 ]][ p[ n ] ] + map[ p[ n ]][ 1 ] < bestL ) ){
                for( int j = 1; j <= n; j++ )
                    bp[ j ] = p[ j ];

                bestL = cuL + map[ p[ n - 1 ]][ p[ n ] ] + map[ p[ n ]][ 1 ];
           }
    }
    else{
        for( int j = i; j <= n; j++ ){
            //判断是否可以进去下一个子树
            if( map[ p[ i - 1 ]][ p [ j ] ] != NOEDGE &&
               ( bestL == NOEDGELENGTH || cuL + map[ p[ j - 1 ]][ p[ j ]] < bestL ) ) {
                    Swap( p[ i ], p[ j ] );
                    cuL += map[ p[ i - 1 ]][ j ];
                    backTrack( i + 1 );
                    cuL -= map[ p[ i - 1 ]][ j ];
                    Swap( p[ i ], p[ j ] );
               }
        }
    }
}
int main()
{
    cin >> n;
    initMap( n );
    backTrack( 2 );
    if( bestL != NOEDGELENGTH )
    {
        cout << bestL << endl;
        for( int i = 1; i <= n; i++ ){
            cout << bp[ i ] << " ";
        }
        cout << endl;
    }
    return 0;
}