后缀数组的DC3构造法
本文的大部分内容都是在理解了这篇文章的大部分内容后而写:http://www.cppblog.com/superKiki/archive/2010/05/15/115421.aspx
在字符串相关的问题中,后缀数组是一种很有效的武器。
后缀数组至少可以解决如下一些问题(当然并不一定是所有下列问题的最优解法):
1. 在一个字符串中找出一个子串,这个子串出现至少2次(或者指定出现k次),且长度最长。(分为可重叠和不可重叠)
2. 在多个字符串中查找最长公共子串。
3. 某个字符串的最长回文子串。
4. 上述问题的变种。
作为一个菜鸟级程序员,对于理解后缀数组这样的算法着实费了不少劲。下面将我看到的和理解的关于后缀数组的内容介绍如下。
后缀数组
后缀数组是一种对字符串所有后缀进行排序得到的数组。比如对于字符串S=banana$,它的所有后缀为:
| 后缀 | i |
| banana$ | 0 |
| anana$ | 1 |
| nana$ | 2 |
| ana$ | 3 |
| na$ | 4 |
| a$ | 5 |
| $ | 6 |
对所有这些后缀进行字典序排序的结果为:
| 后缀 | i |
| $ | 6 |
| a$ | 5 |
| ana$ | 3 |
| anana$ | 1 |
| banana$ | 0 |
| na$ | 4 |
| nana$ | 2 |
如何构造后缀数组
构造后缀数组的算法主要分为:倍增算法、利用后缀树构造后缀数组以及一些递归算法。
本文主要介绍DC3算法,这是一种可以在线性时间内构造后缀数组并且已经有广泛应用的算法。关于该算法原汁原味的介绍为:http://algo2.iti.kit.edu/documents/jacm05-revised.pdf
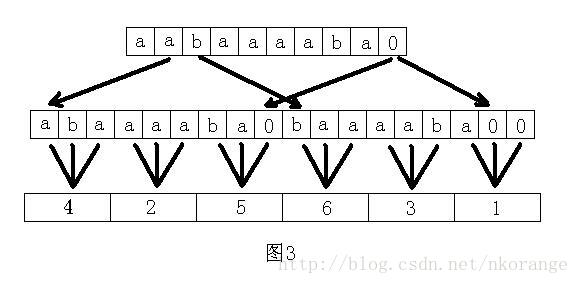
该算法首先将所有后缀分为两部分:后缀起始位置模3为0和后缀起始位置模3不为0。先对模3不为0的后缀进行排序,方法如下图:
将后缀起始位置为1和后缀起始位置为2的两部分连接起来。注意这里连接的两部分后面都添加了0,这是为了让连接的两部分的长度都为3的倍数,这样才能3个字符一组进行合并。我们把诸如"aba","aaa"等字符串整体看成一个字符,那么上面连接后的字符串的长度就缩短为原来的三分之一,对于原始字符串来说,则缩短为三分之二。然后对于合并后的字符串递归进行DC3排序。这样,剩下的问题便是如何在已知后缀起始位置模3不为0的排序后得到模3为0的排序,并与模3不为0的后缀排序进行合并。
首先,对于模3为0的后缀的排序,可以看做是模3为1的后缀加上一个前缀组成的两部分。因此使用一次基数排序就可以完成。
然后,对于合并,可以采用一次简单的归并,因为模3为0的后缀与模3不为0的后缀有简单的转化关系,所以在合理的设计数据结构后可以达到线性复杂度。