【数据结构】Huffman编码
基础知识
目前,进行快速的远距离通信的主要手段是电报,即将需传送的信息转换成由二进制字符组成的字符串。例如,需传送的信息为“ABACCDA”,它只有四个字符,只需要两个字符的串便可以进行编码。假设A、B、C、D的编码分别为00、01、10、11,则上述信息所转换成的电文为“00010010101100”,总长为14位,对方接收到时,可按照二位一分进行译码。
当然,在传送电文时,总希望电文的总长度尽可能的短。如果对每个字符设计长度不等的编码,且让电文中出现次数较多的字符采用尽可能短的编码,则传送电文的总长度便可减少。如果设计A、B、C、D的编码分别为0、00、1和01,则上述信息的电文可转换长度为9的字符串“000011010”。但是这样的电文无法翻译,例如传送过去的前4个字符串的子串“0000”就有多种翻译方法,可以译为“AAAA”、“BB”、“AAB”等等。因此,若要设计长短不一的编码,则必须满足任何一个字符的编码都不是另一个字符的前缀,这种编码称为前缀编码。
可以利用二叉树来设计二进制的前缀编码。例如有图(1)所示一棵二叉树,它的4个叶子节点分别表示A、B、C、D这四个字符,并且约定左分支表示字符‘0’,右分支表示字符‘1’,则可以将从根节点到叶子节点的路径上分支字符组成字符串作为该叶子节点字符的编码。由图(1)可以得到A、B、C、D的二进制前缀编码为0、10、110和111。
图(1)
那么,如何得到使电文总长最短的二进制前缀编码呢?假设每种字符在电文中出现的次数为ωi,其编码长度为ιi,电文中只有n种字符,则电文总长为Σωi*ιi(其中i=1…n)。对应到二叉树上,若置ωi为叶子节点的权值,ιi恰为从根节点到叶子节点的长度,则Σωi*ιi(其中i=1…n)恰为二叉树上带权路径长度。由此可知,设计电文总长最短的二进制前缀编码即转换为以n种字符出现的频率作为权值设计一棵Huffman树的问题,由此得到的二进制前缀编码称为Huffman编码。
Huffman树的构造算法称为Huffman算法,叙述如下:
(1)根据给定的n个权值{ω1,ω2,…,ωn}构成n棵二叉树的集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一 个带权为ωi的根节点,其左右子树均为空。
(2)在F中选取两棵根节点的权值最小的树作为左、右子树构造一棵新的二叉树,且置新的二叉树的根节点的权值为其左、右子树上根节点的权值之和。
(3)在F中删除这两棵树,同时将新得到的二叉树加入到F中。
(4)重复(2)和(3),直到F只含一棵树为止。这棵树便是Huffman树。
Huffman树的构造过程的一个实例如图(2)所示,假设有a、b、c、d四个字符,权值分别为7、5、2和4:
图(2)
代码实现
由于Huffman树中没有度为1的节点(这类树又称为严格的(strict)(或正则的)二叉树),则一棵含有N个叶子节点的Huffman树共有2N-1个节点。可以存储在一个大小为2N-1的一维数组中。
接下来以表(1)所示的字符与频率为例,演示用C语言实现Huffman树的构造、编码及译码过程:
表(1)
1、建立Huffman树
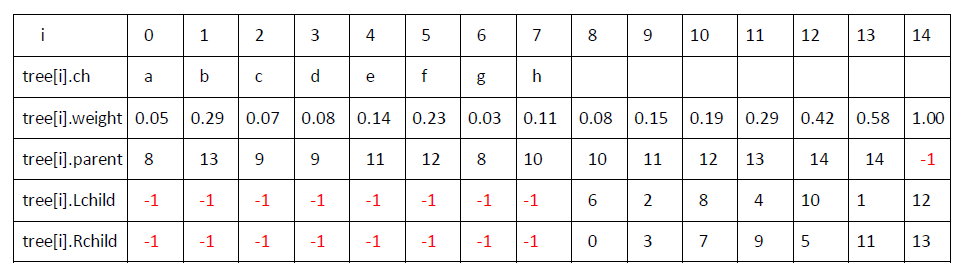
首先建立Huffman树,存储在一维数组tree[M](其中M=2N-1,N=8)中,tree[M]中的每一项存储Huffman树的一个节点信息:字符(ch)、权值(weight)、左、右孩子在tree数组中的下标(Lchild、Rchild)、父节点在tree数组中的下标(parent)。最终构建的Huffman树如图(3)所示:
图(3)
tree[M]数组保存了这棵Huffman树的信息,其内容如表(2)所示:(表中的-1表示左右孩子节点为空(即叶子节点)或是父节点为空,父节点为空的节点为根节点。)
表(2)
2、获取各个字符的Huffman编码
接下来根据建立的Huffman树来获取每个字符的编码,保存到code[N](N为需编码的字符个数,此例中N=8)数组中,code[N]中的每一项存储一个字符的编码信息:字符(ch)、长度为N的位串(bits[N])、字符编码在位串中的起始位置(start,位串下标为start—N的内容为该字符的编码)。
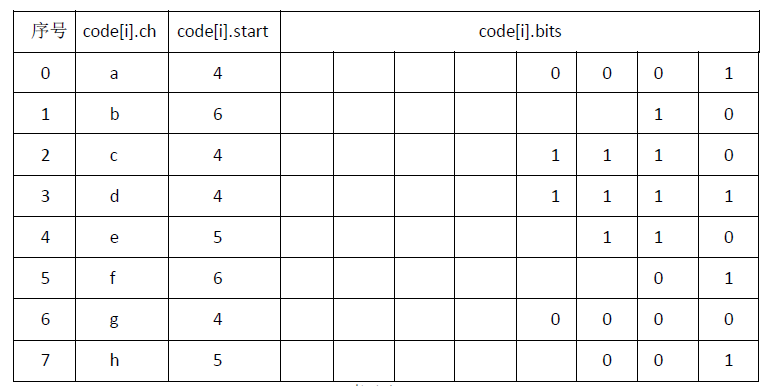
依次从每个叶子节点出发,向上回溯直到根节点,从后往前填写bits[N],获得每个字符的编码,得到的Code[N]内容如表(3)所示:
表(3)
3、编码
例如对字符串A=“bbfehagd”进行编码,仅需根据code数组将A中的每个字符转换成其对应的编码即可。则A转换成的电文为:101001110001000100001111。
4、译码
译码过程需要从建立的Huffman树的根节点出发(即tree[M]数组的第M-1项),从左往右扫描待翻译的“01”电文,若遇‘0’,则走向左孩子;若遇‘1’,则走向右孩子,直到走到叶子节点,该叶子节点所表示的字符即为这一段“01”子串所表示的字符;继而重新从根节点出发,翻译下一段“01”串,直到将待翻译的“01”串扫描完。若字符串读完,还未到叶子节点,则输入电文有错。
例如对上文中编码生成的电文B="101001110001000100001111"的译码过程如图(4)所示: 
(a) (b)
(c) (d)
(e) (f)
(g) (h)
图(4)
代码清单
#include<stdio.h>
#include<stdlib.h>
#define N 8 //叶子总数,即需编码字符的个数
#define M 2*N-1 //节点总数
#define maxval 10000.0 //最大权值
#define maxsize 1000 //数组大小的最大值
typedef struct HuffmanTree//用于存储Huffman树中的节点信息
{
char ch; //字符
float weight; //权值
int Lchild; //左孩子
int Rchild; //右孩子
int parent; //父节点
}HuffmanTree;
typedef struct CodeType//用于存储单个字符的编码结果
{
char ch; //字符
char bits[N]; //位串
int start; //编码在位串中的起始位置
}CodeType;
void CreateHuffmanTree(HuffmanTree tree[]); //创建Huffman树
void HuffmanCode(CodeType code[],HuffmanTree tree[]);//根据Huffman树求出Huffman编码存储在code数组中
void incode(CodeType code[],char *A,char *B); //将字符串A编码,变成“01”串保存在数组B中
void decode(HuffmanTree tree[],char *str); //将“01”字符串str进行译码,直接输出
int main()
{
HuffmanTree tree[M]; //tree存储Huffman树
CodeType code[N]; //code存储单个字符的编码结果
char A[maxsize]; //待编码的字符串
char B[maxsize]; //字符串编码后生成的"01"串
CreateHuffmanTree(tree); //创建Huffman树
HuffmanCode(code,tree); //获得单个字符的编码结果
printf("请输入要编码的字符串:");
gets(A);
incode(code,A,B);//根据单个字符的编码将字符串A编码成字符串B
printf("编码结果为:");
puts(B);
decode(tree,B);//根据Huffman树对编码结果进行翻译,直接输出
return 0;
}
void CreateHuffmanTree(HuffmanTree tree[])
{
int i,j;
int p1,p2; //p1,p2记录最小权值及次小权值节点在数组中的下标
float min1,min2; //min1记录最小权值,min2记录次小权值
for(i=0;i<M;i++) //初始化Huffman树的M个节点
{
tree[i].weight=0.0;
tree[i].Lchild=-1;
tree[i].Rchild=-1;
tree[i].parent=-1;
}
//输入Huffman树前N个节点的信息,即待编码的字符及其权值
printf("请依次输入%d个字符及权值\n",N);
for(i=0;i<N;i++)
{
char c;
float w;
printf("请输入第%d个字符及其对应的权值:",i+1);
scanf("%c %f",&c,&w);
getchar(); //吃掉回车符
tree[i].ch=c;
tree[i].weight=w;
}
//进行N-1次合并,生成N-1个新节点
//每次找到权值最小的两个单个节点(即无父节点的节点)+,合并形成新节点,更改这两个节点的父节点信息、新节点的权值及左右孩子节点信息
for(i=N;i<M;i++)
{
p1=p2=0; //最小权值节点及次小权值节点对应下标初始化为0
min1=min2=maxval; //最小权值及次小权值初始化为权值最大值
for(j=0;j<i;j++) //依次检测Huffman树的前i个节点
{
if(tree[j].parent==-1)//若该节点无父节点
{
if(tree[j].weight<min1)//若该节点的权值小于最小权值,
{ //将最小权值赋给次小权值,该节点的权值赋给最小权值作为最小权值
min2=min1; //并更改对应p1,p2的值,使之指向对应节点的下标
min1=tree[j].weight;
p2=p1;
p1=j;
}
else
{
if(tree[j].weight<min2)//若该节点的权值大于最小权值,小于次小权值,
{ //将该节点的权值赋给次小权值,该节点的下标赋给p2
min2=tree[j].weight;
p2=j;
}
}
}
}
tree[p1].parent=i; //更改权值最小两个节点的父节点信息
tree[p2].parent=i;
tree[i].Lchild=p1;//更改父节点左右孩子信息及权值
tree[i].Rchild=p2;
tree[i].weight=tree[p1].weight+tree[p2].weight;
}
}
void HuffmanCode(CodeType code[],HuffmanTree tree[])//根据Huffman树求出Huffman编码存储在code数组中
{
int i,c,p;
CodeType cd;//缓冲变量
for(i=0;i<N;i++)//依次检测前N个节点,前N个节点为叶子节点,即从Huffman从下往上获得单个字符的编码
{
cd.start=N;
cd.ch=tree[i].ch;
c=i; //c为当前节点
p=tree[i].parent; //p为当前
while(p!=-1)
{
cd.start--;
if(tree[p].Lchild==c)
cd.bits[cd.start]='0';//tree[i]是左子树,生成代码'0'
else
cd.bits[cd.start]='1';//tree[i]是右子树,生成代码'1'
c=p;
p=tree[p].parent;
}
code[i]=cd;//第i+1个字符的编码存入code[i]
}
}
void incode(CodeType code[],char *A,char *B)//编码
{
int i,k=0;
for(i=0;A[i]!='\0';i++)
{
int j=0,p;
while(code[j].ch!=A[i])
j++;
for(p=code[j].start;p<N;p++)
B[k++]=code[j].bits[p];
}
B[k]='\0';//注意!
}
void decode(HuffmanTree tree[],char *str)//译码
{
int j=0,i=M-1;//tree[M-1]为根节点,从根节点开始译码
printf("译码结果为:");
while(str[j]!='\0')
{
if(str[j]=='0')
i=tree[i].Lchild;//走向左孩子
else
i=tree[i].Rchild;//走向右孩子
if(tree[i].Lchild==-1)//tree[i]是叶子节点
{
printf("%c",tree[i].ch);
i=M-1;//回到根节点
}
j++;
}
printf("\n");
if(tree[i].Lchild!=-1&&str[j]!='\0')//字符串读完,但未到叶子节点,则输入电文有错
printf("ERROR!");
}
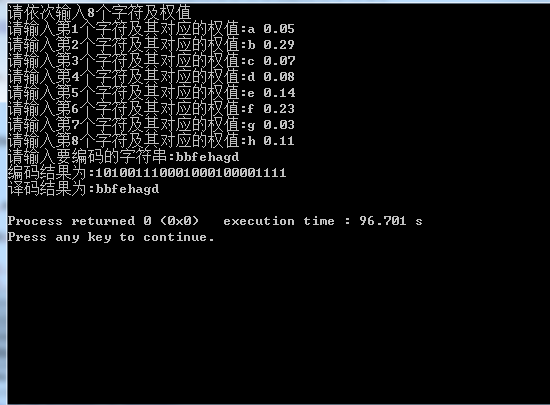
运行结果:
谢谢观赏~~![]()
![]()