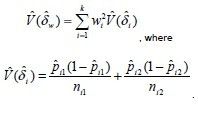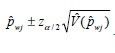Reading "Using SAS/IML to Generate Weighted Chi-Square Statistics"

这篇文章逻辑性很强,脉络清晰,这样的思维能力就是所谓的逻辑了吧.

文章将计算加权卡方统计量分作12个小环节,具体如下:

1.设定矩阵

假设存在一药物作用的患者样本,它有K(1,2,...,K)个观测,两种(i,j)处理,,将所有观测数据写成矩阵形式,就可以得到一个K*2的矩阵

2.计数

要进行卡方统计量的计算,我们首先需要计算行计数和,进而来计算权重,行计数和公式为:

用iml语言可以表示为:ndot= n[,+];

3.比率估计

计算患者药物反应比率的点估计,因为有两种药物处理,所以存在两种处理对应的患者反应情况,再结合K个患者,所以该比率估计也是一个K*2的矩阵

该公式iml语言为:phat= x/n;

4.加权比率

计算每种处理患者反应的加权比率估计,在(3)计算的比率估计基础上考虑两种处理的权重,重新计算得到的比率就是加权估计比率

其数学表达为:

iml中表达为:pbar= (n#phat)[,+]/ndot;

5.权重的计算

我们知道标准的Cochran-Mantel-Haenszel的调和平均公式为:

这个公式比较复杂,可以分别计算分子分母的值,然后再进行除法运算,这样在条理可以很清楚看出:

wnum = n[,#]/ndot;
wden = wnum[+,];
w = wnum/wden;

6.每种处理考虑权重的比率估计,

需要区别的是,前面考虑的权重都是单独的观测,这里是对两种处理的进行加权比率估计,得到的结果应是一个1*2的矩阵.

数学表达式为:

iml表达为:pwt = (w#phat)[+,];

7.计算pwt 估计的方差,pwt方差的计算公式为:

iml中的计算代码为:varpwt = (w#w#phat#(1-phat)/n)[+,];

8.计算两种处理间比率差值,显然其差异为:

由于两种处理在矩阵中就是两列,所起该差值就是两列的差值,iml中计算可以简单的表达为:

deltahat = phat[,2] – phat[,1];

上式计算的差值是矩阵中对应原始的差值,还需要计算两组整体的比率差值:

iml中的表达为:deltawt = (w # deltahat) [+,];

9.计算(8)中估计的方差,我们有方差公式:

iml中写成:

vardeltai = (phat#(1-phat) / n ) [,+];

vardeltaw = (w # w # vardeltai ) [+,];

10.计算pwt的置信区间

数学表达;

iml表达:

pwtcil = pwt – 1.96 * sqrt(varpwt);
pwtciu = pwt + 1.96 * sqrt(varpwt);

11.计算deltawt的置信区间

数学表达:

iml表达:

delwcil = deltawt – 1.96* sqrt(vardeltaw);
delwciu = deltawt + 1.96* sqrt(vardeltaw);

12.两种处理的差异性的假设检验,计算卡方值

iml表达:

chictmp = ((n[,#] # deltahat) / ndot ) [+,];
chicnum = chictmp ** 2;
chicden = (n[,#] # pbar # (1-pbar) / ndot ) [+,];
chic2 = chicnum/chicden;

13计算P值

从服从卡方分布的卡方统计量很容易计算得到相应P值:

pchic2 = 1 – probchi(chic2, 1);

14.整理代码如下

data Matrix;
input tx stratum x n;
datalines;
1 1 140 450
1 2 50 170
1 3 60 200
2 1 180 440
2 2 90 200
2 3 60 180
;
run;
%let alpha=0.05;
proc iml;
   reset print;                               /* sent output to window */
   use Matrix;                                /* specify dataset to read in */
   read all var {x} into x1 where (tx = 1);   /* define matrix x1 from var x*/
   read all var {x} into x2 where (tx = 2);   /* and same for matrix x2 */
   read all var {n} into n1 where (tx = 1);   /* likewise for matrix n1 */
   read all var {n} into n2 where (tx = 2);   /* finally, matrix n2 */
   x = x1 || x2;                             /* Catenate x1 and x2 to get X */
   n = n1 || n2;                             /* Catenate n1 and n2 to get N */
   ndot        = n[,+];                      /* All statements below were */
   phat        = x/n;                        /* previously explained above */
   pbar        = (n#phat)[,+] / ndot;
   wnum        = n[,#] / ndot;
   wden        = wnum[+,];
   w           = wnum / wden;
   pwt         = (w # phat)[+,];
   varpwt      = (w # w # phat # (1-phat) / n)[+,];
   deltahat    = phat[,2] – phat[,1];
   deltawt     = (w # deltahat) [+,];
   vardeltai   = (phat # (1-phat) / n ) [,+];
   vardeltaw   = (w # w # vardeltai ) [+,];
   %let uppera = %sysevalf(1.0-&alpha/2);
   zdot5       = probit(&uppera);
   pwtcil      = pwt - zdot5 * sqrt(varpwt);
   pwtciu      = pwt + zdot5 * sqrt(varpwt);
   delwcil     = deltawt - zdot5 * sqrt(vardeltaw);
   delwciu     = deltawt + zdot5 * sqrt(vardeltaw);
   chictmp     = ( (n[,#] # deltahat) / ndot ) [+,];
   chicnum     = chictmp ** 2;
   chicden     = (n[,#] # pbar # (1-pbar) / ndot ) [+,];
   chic2       = chicnum/chicden;
   pchic2      = 1 – probchi(chic2, 1);
quit;

详见:<Using SAS/IML to Generate Weighted Chi-Square Statistics>