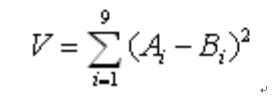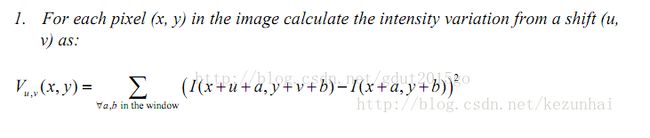图像处理特征不变算子系列之Moravec算子

本文是转载，出自：http://blog.csdn.net/kezunhai

         1977年，Moravec提出了兴趣点（Points ofInterests)的概念，并应用于解决Stanford Cart的导航问题。1981年， Moravec在International Joint Conference on ArtificialIntelligence发表了篇题为：Obstacle Avoidance and Navigation in the RealWorld by a Seeing Robot Rover的文章，并将其应用与立体匹配。本文将主要介绍Moravec算子的点特征提取的原理和过程。

          Moravec的原理如果有一句话来说就是：通过滑动二值矩形窗口寻找灰度变化的局部最大值。具体来说主要包括四个过程：

           1）滑动窗口计算灰度变化（Calculate intensity variantion from shifting windows）

            滑动窗口在现有的技术中已经有了很多应用，如模板匹配、目标检测（hog特征的行人检测）等。在Moravec算子中，一般窗口的大小取3×3、5×5、7×7等等，但是随着窗口的增大，计算量也就越大。Moravec算子通过对窗口的水平、垂直和对角八个方向进行移动（Horizontally、Vertically and four diagonals），计算原窗口与滑动窗口差的平方和来得到灰度的变化。我们进一步通过下图一个3×3的滑窗来进行说明：

上图中，红色框表示的是原始框，而蓝色框表示向右上的滑动框，白色框表示前景255，黑色框表示背景0。那么原始框和滑动框的灰度变化通过对应位置差的平方和来表示，也即通过下式来计算：

同样，根据上式计算另外七个方向滑动框的灰度变化（水平向左、水平向右、垂直向上、垂直向下以及四个对角）。至此，我们就计算完成了8个方向的灰度变化，我们称此操作位Moravec operator（Moravec算子）。

            2）构造角点性映射图（Construct the cornerness map）

            在构造角点映射图之前，我们先来分析下，通过上式的我们可以得到角点吗？或者凭什么通过计算两个框对应位置的差的平方和就可以检测到角点？问题问得好，我们来看下面的图：

上面四张图上的四个红色的框表示我们正在处理的窗，第一幅图中的窗在表示在目标内部或者是背景上，该区域灰度分布均与，通过对其在8个方向上灰度，灰度变化很小；第二幅图中的窗跨在图像的边缘处，当垂直于边缘方向滑动窗口时将会导致灰度的很大变化，而沿着边缘滑动窗时，灰度变化较小；第三幅图中的窗在角点处，不管往哪个方向滑动窗口，都会导致灰度的很大变化；而第四幅图中的框内是一个离散点，滑动窗向任意方向滑动也会导致灰度的很大变化。

           因此，通过上面的描述和分析，我们可以知道，Moravec算子可以作为一种角点性的度量，这种度量是通过求8个方向的滑窗来的最小值来表示。用公式表示如下：

我们通过下图来描述角点映射图的构造：

上图中的是通过Moravec算子计算得到的，其中1表示1*255^2，2表示2*255^2。通过上图可以知道：

       （1）角点位于局部最大值处，我们可以应用非极大值抑制找到局部最大值（non-maximal suppression）。

      （2）离散点（噪声点）与角点有相同的角点性（cornerness），因此Moravec算子对噪声敏感，但是通过增大滑窗的大小可以对噪声起到一定的抑制作用，可同时增加了计算量。另一方面，可以通过设定一个阈值T来对cornerness map进行二值化，小于阈值T的cornerness map设置为0，从而对离散点的局部最大值进行抑制。阈值的选择引用原文的话：Choosing thisthreshold is difficult as it must be set high enough to avoid these falsecorners(isolated pixel), but low enough to retain as many true corners aspossible.

      （3）Moravec算子不能应用与图像边界的一定区域（标记为X的区域），对于这部分区域，一般直接忽略，在cornerness map中这些区域对应的值置0。

         下面对Moravec算子的基本步骤进行简单的总结，其主要包括包括：

 我们再上两张效果图：

        

从上图也可以看到，Moravec算子对角点的检测效果还不错，但是对于对角线上的角点容易出现误检。

          

总结：Moravec算子作为第一个广泛应用的角点检测算法，开创了角点检测的新纪念，后续的很多角点检测算子都是在其基础上通过扩展得到的。但是Moravec算子也存在诸如方向各异性、噪声敏感、对旋转不具备不变形（角点不具备repeatability）、滑动窗内的各个像素权重同质性（中心像素权重大，离中心越远，权重越小）。在下一篇中，我将介绍一种对Moravec算子进行改进、在很多领域取得非常广泛应用的另一种算子-----Harris算子。

        另外可以参考：

               http://code.google.com/p/jfeaturelib/wiki/Moravec（可以现在Moravec算子的库和源代码）

               http://kiwi.cs.dal.ca/~dparks/CornerDetection/moravec.htm （Moravec算子的更细节内容）