最小生成树prim算法

Agri-Net

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 49246		Accepted: 20445

Description

Farmer John has been elected mayor of his town! One of his campaign promises was to bring internet connectivity to all farms in the area. He needs your help, of course. 
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms. 
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm. 
The distance between any two farms will not exceed 100,000. 

Input

The input includes several cases.

For each case, the first line contains the number of farms, N (3 <= N <= 100). The following lines contain the N x N conectivity matrix, where each element shows the distance from on farm to another. Logically, they are N lines of N space-separated integers. Physically, they are limited in length to 80 characters, so some lines continue onto others. Of course, the diagonal will be 0, since the distance from farm i to itself is not interesting for this problem.

Output

For each case, output a single integer length that is the sum of the minimum length of fiber required to connect the entire set of farms.

Sample Input

4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0

Sample Output

28

So

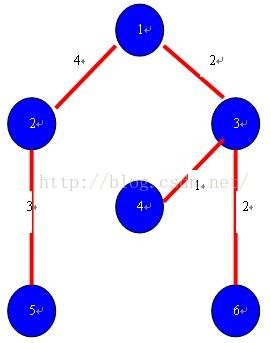
所谓生成树，就是n个点之间连成n-1条边的图形。而最小生成树，就是权值（两点间直线的值）之和的最小值。

  

 首先，要用二维数组记录点和权值。如上图所示无向图：
       int map[7][7];
       map[1][2]=map[2][1]=4;
       map[1][3]=map[3][1]=2;
       ......


      然后再求最小生成树。具体方法是：


1.先选取一个点作起始点，然后选择它邻近的权值最小的点（如果有多个与其相连的相同最小权值的点，随便选取一个）。如1作为起点。


visited[1]=1;
pos=1;
//用low[]数组不断刷新最小权值，low[i](0<i<=点数)的值为：i点到邻近点（未被标记）的最小距离。
low[1]=0;  //起始点i到邻近点的最小距离为0
low[2]=map[pos][2]=4;
low[3]=map[pos][3]=2;
low[4]==map[pos][4]=3;
low[5]=map[pos][5]=MaxInt;  //无法直达
low[6]=map[pos][6]=MaxInt;

  2.再在伸延的点找与它邻近的两者权值最小的点。


//low[]以3作当前位置进行更新


visited[3]=1;


pos=3;


low[1]=0;   //已标记，不更新


low[2]=map[1][2]=4;  //比5小，不更新


low[3]=2;  //已标记，不更新


low[4]=map[1][4]=3;   //比1大，更新后为：low[4]=map[3][4]=1;


low[5]=map[1][5]=MaxInt;//无法直达，不更新


low[6]=map[1][6]=MaxInt;//比2大，更新后为：low[6]=map[3][6]=2;

获取权值最小的一棵树：

当所有点都连同后，结果最生成树如上图所示。

     所有权值相加就是最小生成树，其值为2+1+2+4+3=12。

     至于具体代码如何实现，现在结合POJ1258例题解释。代码如下：

#include <stdio.h>
#include <string.h>
#define MaxInt 0x3f3f3f3f
#define N 110
//创建map二维数组储存图表，low数组记录每2个点间最小权值，visited数组标记某点是否已访问
int  map[N][N],low[N],visited[N];
int  n;

int  prim()
{
    int  i,j,pos,min,result=0;
    memset (visited,0, sizeof (visited));
//从某点开始，分别标记和记录该点
    visited[1]=1;pos=1;
//第一次给low数组赋值
    for (i=1;i<=n;i++)
        if (i!=pos) low[i]=map[pos][i];
//再运行n-1次
    for (i=1;i<n;i++)
    {
//找出最小权值并记录位置
     min=MaxInt;
     for (j=1;j<=n;j++)
         if (visited[j]==0&&min>low[j])
         {
             min=low[j];pos=j;
         }
//最小权值累加
    result+=min;
//标记该点
    visited[pos]=1;
//更新权值
    for (j=1;j<=n;j++)
        if (visited[j]==0&&low[j]>map[pos][j])
            low[j]=map[pos][j];
    }
    return  result;
}

int  main()
{
    int  i,v,j,ans;
    while ( scanf ( "%d" ,&n)!=EOF)
    {
//所有权值初始化为最大
        memset (map,MaxInt, sizeof (map));
        for (i=1;i<=n;i++)
            for (j=1;j<=n;j++)
            {
                scanf ( "%d" ,&v);
                map[i][j]=map[i][j]=v;
            }
            ans=prim();
            printf ( "%d\n" ,ans);
    }
    return  0;
}