BestCoder Round #75 1003 - King's Order & 1004 - King's Game

King's Order

 

 Accepts: 381

 

 Submissions: 1361

 Time Limit: 2000/1000 MS (Java/Others)

 

 Memory Limit: 65536/65536 K (Java/Others)

Problem Description

After the king's speech , everyone is encouraged. But the war is not over. The king needs to give orders from time to time. But sometimes he can not speak things well. So in his order there are some ones like this: "Let the group-p-p three come to me". As you can see letter 'p' repeats for 3 times. Poor king!

Now , it is war time , because of the spies from enemies , sometimes it is pretty hard for the general to tell which orders come from the king. But fortunately the general know how the king speaks: the king never repeats a letter for more than 3 times continually .And only this kind of order is legal. For example , the order: "Let the group-p-p-p three come to me" can never come from the king. While the order:" Let the group-p three come to me" is a legal statement.

The general wants to know how many legal orders that has the length of n

To make it simple , only lower case English Letters can appear in king's order , and please output the answer modulo $1000000007$

We regard two strings are the same if and only if each charactor is the same place of these two strings are the same.

Input

The first line contains a number $T(T\le 10)$——The number of the testcases.

For each testcase, the first line and the only line contains a positive number $n(n\le 2000)$.

Output

For each testcase, print a single number as the answer.

Sample Input

2
2
4

Sample Output

676
456950

hint:
All the order that  has length 2 are legal. So the answer is 26*26.

For the order that has length 4. The illegal order are : "aaaa" , "bbbb"…….."zzzz" 26 orders in total. So the answer for n == 4 is 26^4-26 = 456950

数位dp，三维数组 $d[i][j][k]$为处理完 $i$ 个字符 , 结尾字符为 ′a′j​′​​a​′​​+j , 结尾部分已重复出现了 $k$ 次的方案数。转移时当k>=2时，时，d[i][j][k]=d[i-1][j][k-1].

k=1时，d[i][j][1]将d[i-1]中各个字母结尾的各种长度加起来即可。

#include <algorithm>
#include <iostream>
#include <sstream>
#include <cstring>
#include <cstdlib>
#include <string>
#include <vector>
#include <cstdio>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
using namespace std;
#define INF 0x3f3f3f3
const int N=30;
const int mod=1e9+7;

int d[2001][27][4],n;

int main(){
    int t;
    cin>>t;
    memset(d, 0, sizeof(d));
    for (int i=1; i<=26; i++) {
        d[1][i][1]=1;
    }
    for (int i=2; i<=2000; i++) {
        for (int j=1; j<=26; j++) {
            for (int k=1; k<=26; k++) {
                if (k==j) continue;
                for (int g=1; g<=3&&g<=i; g++) {
                    d[i][j][1]+=d[i-1][k][g];
                    d[i][j][1]%=mod;
                }
                
            }
            for (int k=2; k<=3&&k<=i; k++) {
                d[i][j][k]=d[i-1][j][k-1];
            }
        }
    }
    while (t--) {
        scanf("%d",&n);
        int sum=0;
        for (int i=1; i<=26; i++) {
            for ( int j=1; j<=3; j++) {
                sum+=d[n][i][j];
                sum%=mod;
            }
        }
        printf("%d\n",sum);
    }
    return 0;
}

King's Game

 

 Accepts: 249

 

 Submissions: 671

 Time Limit: 2000/1000 MS (Java/Others)

 

 Memory Limit: 65536/65536 K (Java/Others)

Problem Description

In order to remember history, King plans to play losephus problem in the parade gap.He calls $n(1\le n\le 5000)$ soldiers, counterclockwise in a circle, in label $1,2,3...n$.

The first round, the first person with label $1$ counts off, and the man who report number $1$ is out.

The second round, the next person of the person who is out in the last round counts off, and the man who report number $2$ is out.

The third round, the next person of the person who is out in the last round counts off, and the person who report number $3$ is out.

The N - 1 round, the next person of the person who is out in the last round counts off, and the person who report number $n-1$ is out.

And the last man is survivor. Do you know the label of the survivor?

Input

The first line contains a number $T(0<T\le 5000)$, the number of the testcases.

For each test case, there are only one line, containing one integer $n$, representing the number of players.

Output

Output exactly $T$ lines. For each test case, print the label of the survivor.

Sample Input

2
2
3

Sample Output

2
2

Hint:
For test case #1：the man who report number $1$ is the man with label $1$, so the man with label $2$ is survivor.

For test case #1：the man who report number $1$ is the man with label $1$, so the man with label 1 is out. Again the the man with label 2 counts $1$,  the man with label $3$ counts $2$, so the man who report number $2$ is the man with label $3$. At last the man with label $2$ is survivor.

题解都说是约瑟夫问题，可是我并不知道什么是约瑟夫问题……借一下官网题解：

裸的约瑟夫是怎么玩的：$n$ 个人，每隔 $k$ 个删除。

由于我们只关心最后一个被删除的人，并不关心最后的过程，所以，我们没有必要也不能够模拟整个过程。我们用递推解决。假设有$n$个人围成环，标号为$[0,n-1]$从$0$开始的好处是取模方便），每数$k$个人杀一个的情况下，最后一个存活的人的编号是$f[n]$。

我们有$f[1]=0$,这不需要解释。

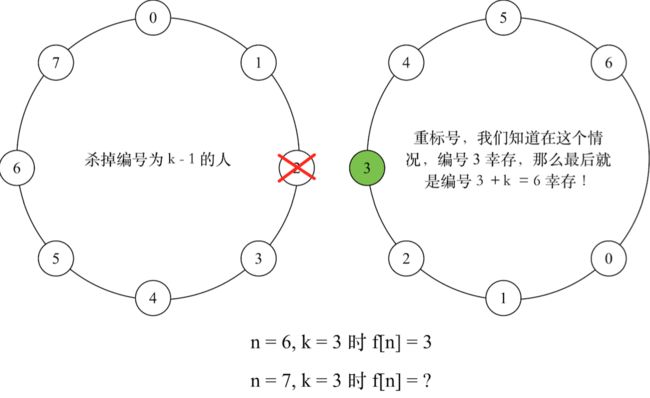
接着考虑一般情况$f[n]$,第一个杀死的人的编号是$k-1$,杀死后只剩下$n-1$个人了，那么我们重新编号！

原来编号为k的现在是$0$号，也就是编号之间相差$3。$我们只要知道现在$n-1$个人的情况最后是谁幸存也就知道$n$个人的情况是谁幸存。幸运的是$f[n-1]$已经算出来了那$f[n]$就是在$f[n-1]$的基础上加上一个$k$即可不要忘记总是要取模。

所以递推式子是： fii1otherf[i]={​​​​​ 0                      i=1​ (f[i - 1] + k) mod i       other​​

此题只用在原版约瑟夫问题上加一维，由于依次隔 $1,2,3...n-1$ 个人删除，所以用 $f[i][j]$ 表示 $i$ 个人，依次隔 $j,j+1...j+i-1$ 个人的幸存者标号。

根据刚才的重标号法，第一次 $j-1$ 号出局，从 $j$ 开始新的一轮，从  $j+1$ 开始清除，剩余 $i-1$ 个人，也有递推式子：

fiji1otherf[i][j]={​​​​​ 0                      i=1​ (f[i - 1][j+1] + j) mod i       other​​

答案就是 $f[n][1]+1$（将标号转移到 $[1,n]$），问题轻松解决。

题意已经说明的很清楚了，解法也很清楚，但题解说的滚动数组就没有悟到，而开5000^2数组爆了内存。后来发现有不用滚动数组的解法，就借来了。具体其实就是一个一个算，并不需要二维数组。学习了一个约瑟夫问题。

#include <algorithm>
#include <iostream>
#include <sstream>
#include <cstring>
#include <cstdlib>
#include <string>
#include <vector>
#include <cstdio>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
using namespace std;
#define INF 0x3f3f3f3
const int N=30;
const int mod=1e9+7;

int f[5005],ans[5005],n;

int solve(int n){
    f[1]=0;
    int k=n-1;
    for (int i=2; i<=n; i++) {
        f[i]=(f[i-1]+(k--))%i;
    }
    return f[n]+1;
}

int main(){
    int t;
    cin>>t;
    memset(f, 0, sizeof(f));
    ans[0]=0;
    ans[1]=1;
    for (int i=2; i<=5000; i++) {
        ans[i]=solve(i);
    }
    while (t--) {
        scanf("%d",&n);
        cout<<ans[n]<<endl;
    }
    return 0;
}