哈弗曼编码及译码

路径长度：从树的一个结点到另一个结点之间边的条数。

树的路径长度：从树根到每个叶子结点之间路径长度之和。

带权树的路径长度：每个叶子结点带有权值，树根到叶子结点的路径长度乘以该叶子结点的权值之和。

哈弗曼树：带权树的路径长度最小的树，又称作最小二叉树和最优二叉树。

哈夫曼树的构造过程：                                                                                                                                                                                 

1.      根据给定的n个带权的结点，构成含有n棵二叉树（每个结点是一棵树）的集合，该树的左右子树均为空。

2.      从含有n棵子树集合中找出两棵权值最小的树最为左右子树构成一个新的二叉树。

3.      从集合中删除这两棵权值最小的二叉树，将新的二叉树插入集合中。

4.      重复2和3步骤，知道最终只剩下一颗树为止，这棵树就是哈弗曼树。

哈弗曼树的应用：最优判定，哈弗曼编码。

前缀编码：字符设计长短不等的编码，且任一字符的编码都不是另一字符编码的前缀（比如0就是00的前缀）。

哈弗曼编码：一种二进制前缀编码。一棵二叉树左分支表示字符“0”，右分支表示字符“1”，从根结点到叶子结点的路径上分支字符组成的字符串作为该叶子结点的编码。求哈弗曼编码就是求一棵哈弗曼树的过程。

由于哈弗曼树中没有度为1的结点二叉树，则一棵有n个叶子的哈弗曼树共有2n-1个结点，可以存储在一个大小为2n-1的一维数组中。构成哈弗曼树后，编码是从叶子结点走出一条叶子结点到根的路径，而译码需从根结点出发走出一条从根到叶子的路径，这两个过程相反，左移编码或者译码时要注意调整二进制存储顺序。

一个字符串得到编码后，以二进制存储时需要额外存储这个字符串的字节数，因为在编码后的编码串转二进制时需要移位，没八个字节转为一个字节，若不满八个字节则需要用0补齐，所以在解码时为了去除掉补齐的0，需要原始字符的字节数，那么假如原始字符串大小为n，字符串编码后的二进制编码大小为m，那么实际二进制编码存储大小为m+1，压缩比就为（m+1）/n。

注意：哈弗曼编码在设计应用的时候需要注意的是编码端和译码端要有相同的字符频率表而且构造哈弗曼树的过程相同，否则没办法译码。

代码实现如下：

// 5.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include <iostream>   
#include <string>      
#include <map> 
using namespace std;
typedef struct
{
	unsigned int weight;
	unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char* *HuffmanCode;

void SelectNode(HuffmanTree &HT,int n,int &Node1,int &Node2)
{
	int i,j;
	for ( i=1;i<=n;i++ )
	{
		if ( !HT[i].parent )
		{
			Node1 = i;
			break;
		}
	}
	for ( j=i+1;j<=n;j++ )
	{
		if ( !HT[j].parent )
		{
			Node2 = j;
			break;
		}
	}
	
	for ( i=1;i<=n;i++ )
		if ( !HT[i].parent && HT[i].weight<HT[Node1].weight && i!=Node2 )
			Node1 = i;
	for ( j=1;j<=n;j++ )
		if ( !HT[j].parent && HT[j].weight<HT[Node2].weight && j!=Node1 )
			Node2 = j;
	if ( HT[Node1].weight > HT[Node2].weight )
	{
		int tmp = Node1;
		Node1 = Node2;
		Node2 = tmp;
	}
		
}
void CreateHFTree(HuffmanTree &HT,int *weight,int n)
{
	if( n<=1 ) return;
	int m = 2*n-1;
	int *w = weight;
	HT = (HuffmanTree)malloc( (m+1)*sizeof(HTNode) );//0号单元未用
	int i = 1;
	for ( ;i<=n;i++ )
	{
		HT[i].weight = weight[i-1];
		HT[i].parent = 0;
		HT[i].lchild = 0;
		HT[i].rchild = 0;
	}
	for ( ;i<=m;i++  )
	{
		HT[i].weight = 0;
		HT[i].parent = 0;
		HT[i].lchild = 0;
		HT[i].rchild = 0;
		
	}
	for ( i=n+1;i<=m;i++ )
	{
		int Node1 = 1;
		int Node2 = 1;
		SelectNode(HT,i-1,Node1,Node2);
		HT[Node1].parent = i;
		HT[Node2].parent = i;
		HT[i].lchild = Node1;
		HT[i].rchild = Node2;
		HT[i].weight = HT[Node1].weight + HT[Node2].weight;
	}
}
void HuffmanEnCode(char ch[],HuffmanTree &HT,map<char,string> &HC,int n)
{
	//+++++++++++++++++++++++从叶子到根逆向求每个字符的哈弗曼编码+++++++++++++++++++++++
	for (int i=1;i<=n;i++ )
	{
		int c = i;
		int f = HT[i].parent;
		for ( ;f!=0;c=f,f=HT[f].parent  )
		{
			if ( HT[f].lchild == c )
				HC[ch[i-1]] = "0" + HC[ch[i-1]];
			else
				HC[ch[i-1]] = "1" + HC[ch[i-1]];
		}
		string s = HC[ch[i-1]];
	}
}
void HuffmanDecode(HuffmanTree &HT,int *w,char *code,int n,char*decode)
{
	int m = 2*n-1;
	int j = 0;
	while( *code )
	{
		int i=m;
		for ( ;HT[i].lchild!=0&&HT[i].rchild!=0; )
		{
			if ( *code=='0' )
				i = HT[i].lchild;
			else
				i = HT[i].rchild;
			++code;
		}
		decode[j++] = HT[i].weight;
	}
}

string B2S( const unsigned char szstr[] ) 
{
	string str;
	for ( int i=0;i<strlen((char*)szstr);i++ )
	{
		int tmp = 128;
		for ( int j=0;j<8;j++ )
		{
			str += (char)(bool)(szstr[i]&tmp) + '0';
			tmp>>=1;
		}
	}
	return str; 
}
unsigned char S2B(char str[])
{
	unsigned char tmp=0;
	for( int i=0;i<8;i++ )
		tmp = (tmp<<1) + (str[i]-'0'); 
	return tmp;
}
int main(int argc, char* argv[])
{
	//++++++++++++字符频率表++++++++++++/
	char chtable[] = {'a','b','c','d'} ;
	int  chfrequency[] ={10,20,30,40};
	int nTableSize = sizeof(chtable);
	//++++++++++++创建Huffman树+++++++++++/
	HuffmanTree HT = NULL;
	map<char,string> HC ;
	CreateHFTree(HT,chfrequency,nTableSize);
	//++++++++++++字符Huffman编码表++++++++++++/
	HuffmanEnCode(chtable,HT,HC,nTableSize);
	//++++++根据字符Huffman编码表对指定字符串进行编码++++++/
	char charSrc[] = "abcdabcdabcd";
	string sencode = "";
	unsigned char encode[255] = {0};
	char buf[9]={0};
	int cnt = 0;
	for ( int i=0;i<strlen(charSrc);i++ )
	{
		sencode += HC[charSrc[i]];
		for ( int j=0;j<HC[charSrc[i]].length();j++ )
		{
			buf[strlen(buf)] = HC[charSrc[i]][j];
			if ( 8 == strlen(buf) )
			{
				encode[cnt] = S2B(buf);
				cnt++;
				memset(buf,0,sizeof(buf));
			}
		}
	}
	if ( strlen(buf)>0 )
	{
		for( i=strlen(buf);i<8;i++ )
			buf[i] = '0';
		int nnnn = strlen(buf);
		encode[cnt] = S2B(buf);
		cnt++;
	}
	encode[cnt] = strlen(charSrc);
	//++++++根据字符Huffman编码表对指定二进制编码字符串进行解码++++++/
	char DecodeArr[255]={0};
	HuffmanDecode(HT,chfrequency,(char*)B2S(encode).c_str(),nTableSize,DecodeArr);
	string sdecode = "";
	int nLen = encode[strlen((char*)encode)-1];
	for ( i=0;i<strlen(DecodeArr);i++ )
	{
		for ( int j=0;j<nTableSize;j++ )
		{
			if ( DecodeArr[i] == chfrequency[j] )
			{
				sdecode += chtable[j];
			}
		}
		if ( sdecode.length() == nLen )
			break;
	}
	//++++++++++++++++++++输出+++++++++++++++++++++++++++++/
	printf("字符及对应的频率为:(a,10),(b,20),(c,30),(d,40)\n");
	printf("----------------------------------------------\n");
	printf("得到的字符Huffman编码表:\n");
	for (int z=0;z<nTableSize;z++)
	{
		printf("%c=%s\n",chtable[z],HC[chtable[z]].c_str());
	}
	printf("----------------------------------------------\n");
	printf("待编码字符串:%s\n",charSrc);
	printf("字符串编码后:%s，长度%d，\n实际存储长度为:%d,因为需要存储原始字符个数.\n",sencode.c_str(),cnt,cnt+1);
	printf("解码后为:%s\n",sdecode.c_str());
	printf("----------------------------------------------\n");
	printf("编码前字符串长度为:%d\n",strlen(charSrc));
	printf("编码后字符串长度为:%d\n",strlen((char*)encode));
	printf("编码后字符串压缩比为:%.2f%%\n",(double)strlen((char*)encode)/(double)strlen(charSrc)*100);
	getchar();
	return 0;
}

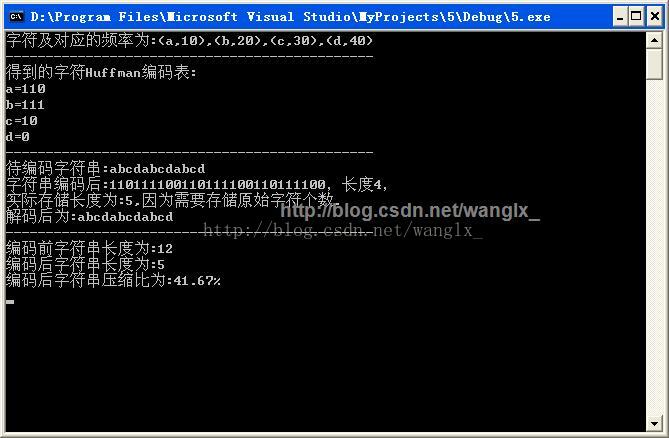
运行结果如下：

拓展及参考：http://blog.csdn.net/xadillax/article/details/6513928

                        数据结构（C语言版） 严蔚敏 吴为民