查找之二分法查找
基本思想:
首先将查找表进行排序
取中间数据元素进行比较
当给定值与中间数据元素的关键字相等时,查找成功
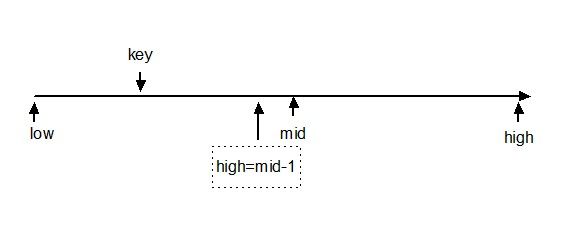
当给定值小于中间元素时, 在中间元素的左区间进行二分查找
当给定值大于中间元素时,在中间元素的右区间进行二分查找
当任意区间均无记录时,查找失败
两种实现方式:递归和非递归
/**
* low:数组的低坐标,high数组的高坐标,key要查找的值
**/
int binary_search( int a[], int low, int high, int key )
{
int ret = -1;
if( a[low] <= key && key <= a[high])
{
if( low <= high )
{
int mid = ( low + high ) / 2;
if( a[mid] == key )
{
ret = mid;
}
else if( key < a[mid] )
{
ret = binary_search( a, low, mid-1, key);
}
else
{
ret = binary_search( a, mid+1, high, key);
}
}
}
return ret;
}
int binary_search2(int a[], int low, int high, int key)
{
int ret = -1;
if( a[low] <= key && key <= a[high] )
{
while( low <= high )
{
int mid = ( low + high ) / 2;
if( a[mid] == key )
{
ret = mid;
break;
}
else if( a[mid] > key )
{
high = mid -1;
}
else if( a[mid] < key )
{
low = mid + 1;
}
}
}
return ret;
}
时间复杂度均是O(logn),但是非递归方式避免了大量的压栈出栈操作,对于数据量比较大时,节省了不少时间
对二分法查找的改进:插值查找
二分法查找时对于中间值mid的求取是:mid = ( low + high ) / 2; 可以变换为 mid = low + 1/2( high - low );对于1/2的选取是默认要查找的值在中间值到左右两个区间的概率各占50%。但是有些特殊情况,要查找的值接近最低端,或者接近最高端时,这样查找的次数就会增多。所以动态的选择这个概率因子可以减少查找的次数。
计算公式:( key - a[low] ) / ( a[high] - a[low] ) ; 即key值的左区间占整个区间的概率, 在概率值附近选取mid更加接近key,所以mid值为:
mid = low + ( high - low ) * ( ( key - a[low] ) / ( a[high] - a[low] ) );
实现代码:
int interpolation_search(int a[], int low, int high, int key)
{
int ret = -1;
if( a[low] <= key && key <= a[high] )
{
while( (low <= high) )
{
float fx = 1.0f * ( key - a[low] ) / ( a[high] - a[low] );
int mid = low + fx*( high - low );
if( a[mid] == key)
{
ret = mid;
break;
}
else if( a[mid] > key )
{
high = mid - 1;
}
else if( a[mid] < key )
{
low = mid + 1;
}
}
}
return ret;
}
时间复杂度还是O(logn),但是该算法用到较多的除法运算和浮点型数值,这样时间上也会耗费不少的时间,所以要考虑设备硬件对浮点型的支持性。