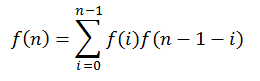2014年第五届蓝桥杯C/C++程序设计本科B组决赛 出栈次序(结果填空)
2014年第五届蓝桥杯C/C++程序设计本科B组决赛题目汇总:
http://blog.csdn.net/u014552756/article/details/51395463
出栈次序
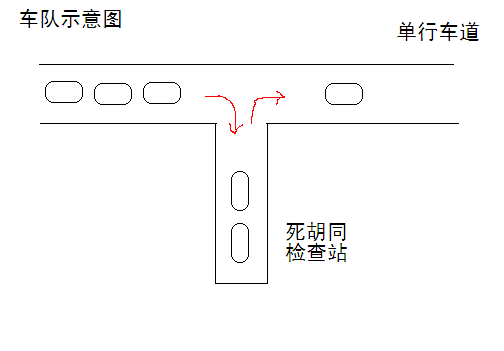
X星球特别讲究秩序,所有道路都是单行线。一个甲壳虫车队,共16辆车,按照编号先后发车,夹在其它车流中,缓缓前行。路边有个死胡同,只能容一辆车通过,是临时的检查站,如图【p1.png】所示。
X星球太死板,要求每辆路过的车必须进入检查站,也可能不检查就放行,也可能仔细检查。
如果车辆进入检查站和离开的次序可以任意交错。那么,该车队再次上路后,可能的次序有多少种?
为了方便起见,假设检查站可容纳任意数量的汽车。
显然,如果车队只有1辆车,可能次序1种;2辆车可能次序2种;3辆车可能次序5种。
现在足足有16辆车啊,亲!需要你计算出可能次序的数目。
题意:求n个元素的出栈情况有多少种。
思路:
方法一:
我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出:
f(1)= 1 //即 1
f(2)= 2 //即 12、21
f(3)= 5 //即 123、132、213、321、231
然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d, 那么考虑:元素a只可能出现在1号位置,2号位置,3号位置和4号位置(很容易理解,一共就4个位置,比如abcd,元素a就在1号位置)。
分析:
1) 如果元素a在1号位置,那么只可能a进栈,马上出栈,此时还剩元素b、c、d等待操作,就是子问题f(3);
2) 如果元素a在2号位置,那么一定有一个元素比a先出栈,即有f(1)种可能顺序(只能是b),还剩c、d,即f(2), 根据乘法原理,一共的顺序个数为f(1)* f(2);
3) 如果元素a在3号位置,那么一定有两个元素比1先出栈,即有f(2)种可能顺序(只能是b、c),还剩d,即f(1),
根据乘法原理,一共的顺序个数为f(2) * f(1);
4) 如果元素a在4号位置,那么一定是a先进栈,最后出栈,那么元素b、c、d的出栈顺序即是此小问题的解,即 f(3);
结合所有情况,即f(4) = f(3) +f(2) * f(1) + f(1) * f(2) + f(3);
为了规整化,我们定义f(0) = 1;于是f(4)可以重新写为:
f(4) = f(0)*f(3) + f(1)*f(2) + f(2) * f(1)+ f(3)*f(0)
然后我们推广到n,推广思路和n=4时完全一样,于是我们可以得到:
f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... +f(n-1)*f(0)
方法二:Catalan数:C(2n,n)/(n+1) (C(2n,n)表示2n里取n)或者C(2n,n)-C(2n,n-1)都可以解决。
参考博客:http://blog.csdn.net/zyearn/article/details/7758716
答案:35357670
#include <iostream>
#include <string.h>
using namespace std;
int main()
{
int f[20];
memset(f,0,sizeof(f));
f[0]=1;
f[1]=1;
f[2]=2;
f[3]=5;
for(int i=4; i<=16; i++)
{
for(int j=0; j<=i-1; j++)
f[i]+=f[j]*f[i-1-j];
}
cout<<f[16]<<endl;
return 0;
}