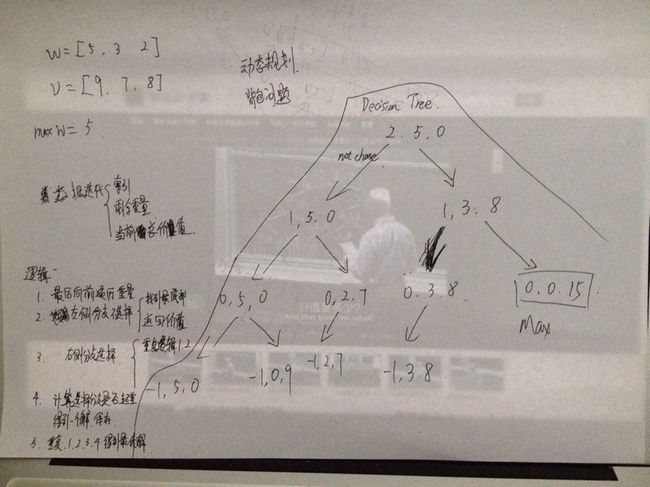
python 版 动态规划 背包问题算法

演示示例

代码

version版本修改增加优化重叠子问题的解决

numCount = 0

#version 1
def MaxVal1(w, v, index, last):
    """
    得到最大价值
    w为widght
    v为value
    index为索引
    last为剩余重量
    """
    global numCount
    numCount = numCount + 1

    #最底部
    if index == 0:
        #是否可以装入
        if w[index] <= last:
            return v[index]
        else:
            return 0

    #寻找可以装入的分支
    without_l = MaxVal1(w, v, index - 1, last)

    #如果当前的分支大于约束
    #返回历史查找的最大值
    if w[index] > last:
        return without_l
    else:
        #当前分支加入背包，剪掉背包剩余重量，继续寻找
        with_l = v[index] + MaxVal1(w, v , index - 1, last - w[index])

    #比较最大值
    return max(with_l , without_l)

#version 2
def MaxVal2(memo , w, v, index, last):
    """
    得到最大价值
    w为widght
    v为value
    index为索引
    last为剩余重量
    """


    global numCount
    numCount = numCount + 1

    try:
        #以往是否计算过分支，如果计算过，直接返回分支的结果
        return memo[(index , last)]
    except:
        #最底部
        if index == 0:
            #是否可以装入
            if w[index] <= last:
                return v[index]
            else:
                return 0

        #寻找可以装入的分支
        without_l = MaxVal2(memo , w, v, index - 1, last)

        #如果当前的分支大于约束
        #返回历史查找的最大值
        if w[index] > last:
            return without_l
        else:
            #当前分支加入背包，剪掉背包剩余重量，继续寻找
            with_l = v[index] + MaxVal2(memo , w, v , index - 1, last - w[index])

        #比较最大值
        maxvalue = max(with_l , without_l)
        #存储
        memo[(index , last)] = maxvalue
        return maxvalue

w = [5, 5, 1, 9 , 10 ,3, 8, 6, 4 , 2, 5, 5, 1, 9 , 10 ,3, 8, 6, 4 , 2]
v = [7, 7, 6, 5, 4, 8, 11, 4, 2, 3,7, 7, 6, 5, 4, 8, 11, 4, 2, 3]

print MaxVal1(w, v, len(w) - 1, 35) , "caculate count : ", numCount

numCount = 0
memo = {}
print MaxVal2(memo , w, v, len(w) - 1, 35) , "caculate count : ", numCount

计算结果

66 caculate count :  188174
66 caculate count :  1134