SVM实现多分类的程序基础工作(三)——基于纠错编码的SVM多类分类算法和基于二叉树的多类SVM算法的基本思想
SVM(支持向量机)最初是针对二分类问题而提出来的,但现在我们要实现多分类,那么可不可以运用SVM呢?根据目前的研究,我们有两种解决途径:
1、 通过构造多个SVM二值分类器并将让它们组合起来实现多类分类,例如one-against-rest, one-against-one和DA GSVM. 虽然这三种方法是当前最常用且性能较优的, 但one-against-rest 和one-against-one方法的泛化误差是无界的. one-against-one所需构造的子分类器的数量关于类别数k 成超线性增长, 共k(k- 1)/2个, 且在测试阶段, 都必须计算所有子分类判据函数. One-against-one方法还有一个最明显的缺点就是, 每个子分类器必须都要非常仔细地调整, 如果某个子分类器不规范化, 则整个分类系统将趋于过学习. DA GSVM方法解决了不可分区域问题, 而且不一定要计算所有的子分类判决函数, 但各个子分类器在有向无环图中的位置也会对分类系统产生较大的影响.
2、 另一种是直接在一个优化公式中同时考虑所有子分类器的参数优化,严格的讲,其思想类似于one-against-rest,只不过是把K个二值SVM优化问题放在一个最优化公式中同时优化,所以它也存在one-against-rest方法相同的缺点,在最优化问题求解过程中的变量远远多于第一种,训练速度不及第一种,在分类精度上也不占优势,特别是在训练样本很大的时候。
基于此基础知识,今天我们来看一下研究人员们在此基础上做了哪些改进工作,下面我将重点介绍一下基于纠错编码的SVM多类分类算法和基于二叉树的多类SVM。
一、 基于纠错编码的SVM多类分类算法
首先我们需了解纠错编码是一种把多类分类问题转化为多个两类分类问题的方法。K类数据分类问题,对每个类进行长度为L 的二进制编码,就把类分类问题转化为L个两类分类问题。由于每个码位上的分类器只需要做两类分类,所以可以采用SVM作为码位分类器。对于一个新样本,L个SVM的分类结果构成一个码字s,K 个编码中与s汉明距离最小的码字所代表的类别就是这个新样本所属类别。把对数据进行ECC编码后,采用SVM作为码位分类器的多类分类方法称为ECC—SVM多类分类算法。有效的ECC编码必须满足两个条件:①编码矩阵的行之间不相关;②编码矩阵的列之间不相关且不互补。因此对于K类分类问题,编码长度L必须满足log2K<K <2 K-1。当然如果你没有任何的基础知识,那么你现在看这段话,你很可能看不懂,那么下面请结合下面的例子再来看上面这段文字吧。
下图是应用纠错编码向量机(Error—Correcting Codes SVM)对5类别进行分类的一个例子。这里取码长L为10bit(3<=L<=15均可)。
首先5类问题,每类问题都用10bit 位进行二进制编码:
1类问题编码后,码字为S1:0111111111
2类问题编码后,码字为S2:1000111111
3类问题编码后,码字为S3:1111000011
4类问题编码后,码字为S4:1011001100
5类问题编码后,码字为S5:0101010101
目前就将5类分类问题转化为10个两类分类问题。由于每个码位上的分类器只需要做两类分类,所以可以采用SVM作为码位分类器,即需10个分类器。
对于一个新样本,10个SVM的分类结果构成一个码字S,5 个编码中与S汉明距离最小的码字所代表的类别就是这个新样本所属类别。ECC—SVM算法中,第i个SVM训练样本的组成是把编码矩阵中第i列取值为0的所有类别的样本归为第1类,把取值为1的所有类别的样本归为第2类。
PS: 汉明距离是什么?
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。 例如:
1011101 与 1001001 之间的汉明距离是 2。
2143896 与 2233796 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
汉明重量是字符串相对于同样长度的零字符串的汉明距离,也就是说,它是字符串中非零的元素个数:对于二进制字符串来说,就是 1 的个数,所以 11101 的汉明重量是 4。
二、基于二叉树的多类SVM
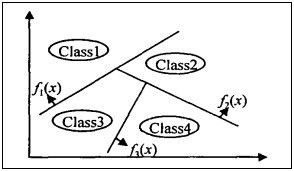
为了更加直观的阐述清楚什么是基于二叉树的多类SVM,下面我们来看下面的一幅图:
从上面我们很容易的看到,是将4类问题(class1,class2,class3,class4)分类,需多少个分隔线(面)把他们分来呢,当然非常直观,4类问题有3个分隔线(面)。并且我们可观察得知:1类和2、3、4类通过f1(x)区别开;剩下没区别开的3类(class2,class3,class4)又通过f2(x)进行区别,即2类和3、4类区别开;剩下的2类通过f3(x)分类。分隔顺序很明显为:1、2、4、3.这种方法实质上就是我们上面提到方法中的one-against-rest。
提到这里有点点认知了吧,那我们作一定的归纳:基于二叉树的多类SVM是先将所有类别分成两个子类, 再将子类进一步划分成两个次级子类, 如此循环下去, 直到所有的节点都只包含一个单独的类别为止, 此节点也是决策树中的叶子. 该方法将原有的多类问题同样分解成了一系列的两类分类问题, 其中两个子类间的分类函数采用SVM. 二叉树方法可以避免传统方法的不可分情况, 并且只需构造k- 1个SVM分类器, 测试时并不一定需要计算所有的分类器判别函数, 从而可节省测试时间.
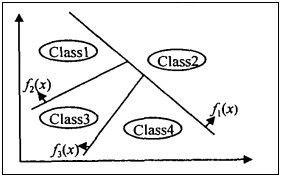
上图中的分隔顺序会不会因为二叉树的结构导致不同呢?
由上图很明显的知道,分隔顺序为2、1、3、4. 上面2个图比较可知,分隔顺序不一样,每个类的分隔区域也不相同,因此,二叉树分类方法的每个类的区域依赖于二叉树的结构,主要是二叉树节点所代表的二值分类器的位置。
二叉树的结构有两种: 一种是在每个内节点处, 由一个类与剩下的类构造分割面; 另一种是在内节点处, 可以是多个类与多个类的分割.
我们一般应用的是one-against-rest方法,即每次分割只分割出一个类. 基于二叉树的多类SVM, 在测试阶段类似DA GSVM, 从根节点开始计算决策函数, 根据值的正负决定下一节点.如此下去, 直到到达某一叶节点为止, 此叶节点所代表的类别就是测试样本的所属类别.
相关文献指出, 越上层节点的分类性能对整个分类模型的推广性影响越大. 因此,在生成二叉树的过程中, 应该让最易分割的类最早分割出来, 即在二叉树的上层节点处分割.