LevenbergMarquardt 算法 eigen实现（c++）

VS2013 PCL1.7.2 使用自带eigen库

#include <iostream>
#include <Eigen/Dense>
#include <unsupported/Eigen/NonLinearOptimization>

struct MyFunctor
{
    int operator()(const Eigen::VectorXf &x, Eigen::VectorXf &fvec) const
    {
        double tmp1, tmp2, tmp3;
        static const double y[15] = { 1.4e-1, 1.8e-1, 2.2e-1, 2.5e-1, 2.9e-1, 3.2e-1, 3.5e-1,
            3.9e-1, 3.7e-1, 5.8e-1, 7.3e-1, 9.6e-1, 1.34, 2.1, 4.39 };

        for (int i = 0; i < values(); i++)
        {
            tmp1 = i + 1;
            tmp2 = 16 - i - 1;
            tmp3 = (i >= 8) ? tmp2 : tmp1;
            fvec[i] = y[i] - (x[0] + tmp1 / (x[1] * tmp2 + x[2] * tmp3));
        }

        return 0;
    }


    int df(const Eigen::VectorXf &x, Eigen::MatrixXf &fjac) const
    {
        double tmp1, tmp2, tmp3, tmp4;
        for (int i = 0; i < values(); i++)
        {
            tmp1 = i + 1;
            tmp2 = 16 - i - 1;
            tmp3 = (i >= 8) ? tmp2 : tmp1;
            tmp4 = (x[1] * tmp2 + x[2] * tmp3); tmp4 = tmp4*tmp4;
            fjac(i, 0) = -1;
            fjac(i, 1) = tmp1*tmp2 / tmp4;
            fjac(i, 2) = tmp1*tmp3 / tmp4;
        }
        return 0;
    }

    int inputs() const { return 3; }
    int values() const { return 3; } // number of constraints
};


int main(int argc, char *argv[])
{
    Eigen::VectorXf x(3);
    x(0) = 10;
    x(1) = -2;
    x(2) = 3;
    //x(2) = 0;

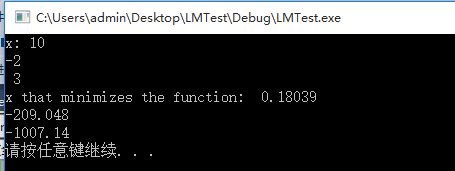
    std::cout << "x: " << x << std::endl;

    MyFunctor functor;
    Eigen::LevenbergMarquardt<MyFunctor, float> lm(functor);

    lm.minimize(x);

    std::cout << "x that minimizes the function: " << x << std::endl;

    system("pause");
    return 0;
}

结果

sample2：(只参考一下啦)

#include <iostream>
#include <Eigen/Dense>
#include <unsupported/Eigen/NonLinearOptimization>
#include "mex.h"
 class pH_Module { // Functor private: double H, H2CO3, HCO3, CO2, CO3, NH3, NH4, HS, H2S, OH; double Fe, Ca, NO3, SO4, PO4; double Kc0, Kc1, Kc2, Knh, Khs, Kw; public: pH_Module(Eigen::VectorXf x0, Eigen::VectorXf other_conc) { H = x0(0)*x0(0); HCO3 = x0(1)*x0(1); CO2 = x0(2)*x0(2); CO3 = x0(3)*x0(3); NH3 = x0(4)*x0(4); NH4 = x0(5)*x0(5); HS = x0(6)*x0(6); H2S = x0(7)*x0(7); OH = x0(8)*x0(8); H2CO3 = x0(9)*x0(9); Fe = other_conc(0)*other_conc(0); Ca = other_conc(1)*other_conc(1); NO3 = other_conc(2)*other_conc(2); SO4 = other_conc(3)*other_conc(3); PO4 = other_conc(4)*other_conc(4); Kc0 = 1.7 *pow(10.0, -3.0); Kc1 = 5.01 *pow(10.0, -7.0) *pow(10.0, 6.0); Kc2 = 4.78 *pow(10.0, -11.0)*pow(10.0, 6.0); Knh = 5.62 *pow(10.0, -10.0)*pow(10.0, 6.0); Khs = 1.3 *pow(10.0, -7.0) *pow(10.0, 6.0); Kw = pow(10, -14)*pow(10, 12); }; int operator()(const Eigen::VectorXf &x, Eigen::VectorXf &fvec) const; int df(const Eigen::VectorXf &x, Eigen::MatrixXf &fjac) const; int inputs() const;// inputs is the dimension of x. int values() const; // "values" is the dimension of F }; int pH_Module::operator()(const Eigen::VectorXf &x, Eigen::VectorXf &fvec) const { // Equations: fvec(0) = x(9)*x(9) - Kc0*x(2)*x(2); fvec(1) = x(0)*x(0)*x(1)*x(1) - Kc1*x(9)*x(9); fvec(2) = x(0)*x(0)*x(3)*x(3) - Kc2*x(1)*x(1); fvec(3) = x(0)*x(0)*x(4)*x(4) - Knh*x(5)*x(5); fvec(4) = x(0)*x(0)*x(6)*x(6) - Khs*x(7)*x(7); fvec(5) = x(0)*x(0)*x(8)*x(8) - Kw; fvec(6) = x(4)*x(4) + x(5)*x(5) - NH4 - NH3; fvec(7) = x(6)*x(6) + x(7)*x(7) - HS - H2S; fvec(8) = x(3)*x(3) + x(1)*x(1) + x(2)*x(2) + x(9)*x(9) - CO3 - HCO3 - CO2 - H2CO3; fvec(9) = x(0)*x(0) + x(5)*x(5) + 2 * Fe + 2 * Ca - (x(1)*x(1) + 2 * x(3)*x(3) + x(6)*x(6) + x(8)*x(8) + NO3 + 2 * SO4 + 3 * PO4); return 0; } int pH_Module::df(const Eigen::VectorXf &x, Eigen::MatrixXf &fjac) const { // Implement Jacobian // row #0 fjac(0, 0) = 0; fjac(0, 1) = 0; fjac(0, 2) = -2 * Kc0*x(2); fjac(0, 3) = 0; fjac(0, 4) = 0; fjac(0, 5) = 0; fjac(0, 6) = 0; fjac(0, 7) = 0; fjac(0, 8) = 0; fjac(0, 9) = 2 * x(9); // row #1 fjac(1, 0) = 2 * x(0)*x(1)*x(1); fjac(1, 1) = 2 * x(0)*x(0)*x(1); fjac(1, 2) = 0; fjac(1, 3) = 0; fjac(1, 4) = 0; fjac(1, 5) = 0; fjac(1, 6) = 0; fjac(1, 7) = 0; fjac(1, 8) = 0; fjac(1, 9) = -2 * Kc1*x(9); // row #2 fjac(2, 0) = 2 * x(0)*x(3)*x(3); fjac(2, 1) = -2 * Kc2*x(1); fjac(2, 2) = 0; fjac(2, 3) = 2 * x(0)*x(0)*x(3); fjac(2, 4) = 0; fjac(2, 5) = 0; fjac(2, 6) = 0; fjac(2, 7) = 0; fjac(2, 8) = 0; fjac(2, 9) = 0; // row #3 fjac(3, 0) = 2 * x(0)*x(4)*x(4); fjac(3, 1) = 0; fjac(3, 2) = 0; fjac(3, 3) = 0; fjac(3, 4) = 2 * x(0)*x(0)*x(4); fjac(3, 5) = -2 * Knh*x(5); fjac(3, 6) = 0; fjac(3, 7) = 0; fjac(3, 8) = 0; fjac(3, 9) = 0; // row #4 fjac(4, 0) = 2 * x(0)*x(6)*x(6); fjac(4, 1) = 0; fjac(4, 2) = 0; fjac(4, 3) = 0; fjac(4, 4) = 0; fjac(4, 5) = 0; fjac(4, 6) = 2 * x(0)*x(0)*x(6); fjac(4, 7) = 2 * Khs*x(7); fjac(4, 8) = 0; fjac(4, 9) = 0; // row #5 fjac(5, 0) = 2 * x(0)*x(8)*x(8); fjac(5, 1) = 0; fjac(5, 2) = 0; fjac(5, 3) = 0; fjac(5, 4) = 0; fjac(5, 5) = 0; fjac(5, 6) = 0; fjac(5, 7) = 0; fjac(5, 8) = 2 * x(0)*x(0)*x(8); fjac(5, 9) = 0; // row #6 fjac(6, 0) = 0; fjac(6, 1) = 0; fjac(6, 2) = 0; fjac(6, 3) = 0; fjac(6, 4) = 2 * x(4); fjac(6, 5) = 2 * x(5); fjac(6, 6) = 0; fjac(6, 7) = 0; fjac(6, 8) = 0; fjac(6, 9) = 0; // row #7 fjac(7, 0) = 0; fjac(7, 1) = 0; fjac(7, 2) = 0; fjac(7, 3) = 0; fjac(7, 4) = 0; fjac(7, 5) = 0; fjac(7, 6) = 2 * x(6); fjac(7, 7) = 2 * x(7); fjac(7, 8) = 0; fjac(7, 9) = 0; // row #8 fjac(8, 0) = 0; fjac(8, 1) = 2 * x(1); fjac(8, 2) = 2 * x(2); fjac(8, 3) = 2 * x(3); fjac(8, 4) = 0; fjac(8, 5) = 0; fjac(8, 6) = 0; fjac(8, 7) = 0; fjac(8, 8) = 0; fjac(8, 9) = 2 * x(9); // row #9 fjac(9, 0) = 2 * x(0); fjac(9, 1) = -2 * x(1); fjac(9, 2) = 0; fjac(9, 3) = -4 * x(3); fjac(9, 4) = 0; fjac(9, 5) = 2 * x(5); fjac(9, 6) = -2 * x(6); fjac(9, 7) = 0; fjac(9, 8) = -2 * x(8); fjac(9, 9) = 0; return 0; } int pH_Module::inputs() const { return 10; } // inputs is the dimension of x. int pH_Module::values() const { return 10; } // "values" is the number of f_i void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[]) { double *data = (double *)mxGetData(prhs[0]); Eigen::VectorXf x0(10); Eigen::VectorXf other_conc(5); // forming vec of unknowns for (int i = 0; i < 10; ++i) { x0(i) = data[i]; } // vec of other ions for (int i = 0; i < 5; ++i) { other_conc(i) = data[i + 10]; } pH_Module functor(x0, other_conc); Eigen::LevenbergMarquardt<pH_Module, float> lm(functor); lm.parameters.xtol = 1e-8; lm.parameters.ftol = 1e-8; int info = lm.minimize(x0); // Assign output plhs[0] = mxCreateDoubleMatrix(1, 10, mxREAL); double * z = mxGetPr(plhs[0]); for (int i = 0; i < 10; ++i) { z[i] = x0(i); } }