背包问题（Knapsack problem）之01

问题描述：

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

转移方程：dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]] + value[i]）

                                          不放                       放入

其中dp[i][j]表示放入i个物品，总价值为j。

代码如下：

// beibaoproblem.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>

using namespace std;


#define max(a, b) ( (a) > (b) ? (a) :(b) )


int _tmain(int argc, _TCHAR* argv[])
{

	const int v = 10;  //最大容量
	const int n = 3;  //物件的个数

	



	int value[] = {4,5,6};
	int weight[] = {3,4,5};
	int temp1, temp2;

	int i,j;

	int dp[n + 1][v + 1];

	//初始化
	for (i = 0; i < n+1; i++)
		for (j = 0; j < v + 1; j++)
		{
			dp[i][j] = 0;
		}
	
	for(i = 1; i <= n; i++)
	{
		for (j = 1; j <= v; j++)
		{
			if (j >= weight[i-1])//表示剩余容量大于第i件的容量，可以放入
			{

				dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i-1]] + value[i-1]);
				
			}
			else              //反之不放入
			{
				dp[i][j] =  dp[i-1][j];
				 
			}
		}

	}


		for (i = 0; i < n+1; i++)
		{
			for (j = 0; j < v + 1; j++)
			{
				cout << dp[i][j]<<" " ;
			}
			cout << endl;
		}

		cout <<  dp[n][v];

	return 0;
}

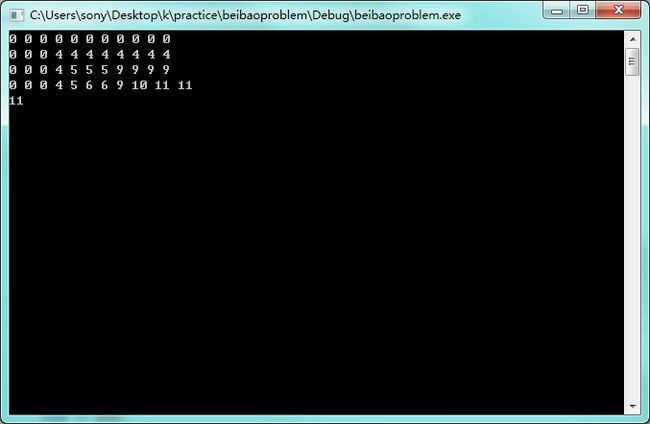
结果：

-----------------------------------------------------------------------------------------------------

以下是从文件读取:

// beibaoproblem.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>

using namespace std;



#define FILENAMELENGTH 1000
#define max(a,b) (a) > (b) ? a : b


class CBeibao
{
public:
	int m_nNumber;     //物品数量
	int m_nMaxWeight;  //最大载重量

	int *m_pWeight;  //每个物品的重量
	int *m_pValue;   //每个物品的价值

	int *m_pCount;   //每个物品被选中的次数
	int m_nMaxValue; //最大价值

public:
	CBeibao(const char* filename);
	~CBeibao();


	int GetMaxValue();
	//n表示物品个数，m背包载重量，w数组重量，v价值数组，c是否被选中数组
	int GetMaxValue(int n, int m, int *w, int *v, int *c); 
	void Display(int nmaxValue);
	void Display(int nMaxValue, const char* filename);

};


//读入数据
CBeibao::CBeibao(const char* filename)
{
	FILE *fp;
	fopen_s(&fp, filename, "r");
	if (fp == NULL)
	{
		printf_s("can not open file");
		return;
	}

	fscanf_s(fp, "%d%d", &m_nNumber, &m_nMaxWeight);

	m_pWeight = new int[m_nNumber+1];
	m_pValue = new int[m_nNumber+1];

	

	//读入每个物品的重量
	m_pWeight[0] = 0;
	for(int i = 1; i <= m_nNumber; i++)
		fscanf_s(fp, "%d", m_pWeight+i);

	//读入每个物品的价值
	m_pValue[0] = 0;
	for(int i = 1; i <=m_nNumber;i++)
		fscanf_s(fp, "%d", m_pValue+i);

	//初始化每个物品被选中次数为0
	m_pCount = new int[m_nNumber+1];
	for(int i = 0; i <=m_nNumber;i++)
		m_pCount[i] = 0;

	fclose(fp);

}

CBeibao::~CBeibao()
{
	delete[] m_pWeight;
	m_pWeight = NULL;

	delete[] m_pValue;
	m_pValue = NULL;

	delete[] m_pCount;
	m_pCount = NULL;

}

int CBeibao::GetMaxValue(int n, int m, int *w, int *v, int *c)//n表示物品个数，m背包载重量，w数组重量，v价值数组，c是否被选中数组
{
	int row = n+1;
	int col = m+1;

	int i,j;

	//value[i][j]表示前i个物品能装入载重量为j的背包中物品的最大价值
	int **value = new int *[row];
	for(i = 0; i < row; i++)
		value[i] = new int[col];
	
	//初始化为0
	for(i = 0; i < row; i++)
		for(j = 0; j < col; j++)
		 value[i][j] = 0;

	//计算
	for(i = 1; i < row; i++)
		for (j = 1; j < col; j++)
		{
			if (j >= w[i])
			{
				value[i][j] = max(value[i-1][j], value[i-1][j - w[i]] + v[i]);
			}
			else
			{
				value[i][j] = value[i-1][j];
			}
		}

	//逆推求装入的物品
		j = m;
		for (i = row - 1; i > 0; i--)
		{
			if (value[i][j] > value[i-1][j])  //表示第i个物品装入
			{
				c[i] = 1;
				j -= w[i];
			}
		}

		//记录最大价值
		int nMaxValue = value[row-1][col-1];

		//释放该二维数组
		for (i = 0; i < row; i++)
		{
			delete[col] value[i];
			value[i] = NULL;
		}

		delete[] value;
		value = NULL;

		return nMaxValue;

}


int CBeibao::GetMaxValue()
{
	int nValue = GetMaxValue(m_nNumber, m_nMaxWeight, m_pWeight, m_pValue, m_pCount);
	m_nMaxValue = nValue;
	return nValue;
}


//显示结果
void CBeibao::Display(int nMaxValue)
{
	_tprintf(_T(" %d"), nMaxValue);
	for(int i = 1; i <= m_nNumber; i++)
	{
		if (m_pCount[i])
		  _tprintf(_T(" %d %d"), i, m_pCount[i]);
	}
	_tprintf(_T(""));
}


void CBeibao::Display(int nMaxValue, const char* filename)
{
	FILE *fp;
	fopen_s(&fp, filename, "w");
	if (fp == NULL)
	{
		_tprintf(_T("can not write file!"));
		return;
	}

	fprintf(fp, "%d", nMaxValue);
	for (int i = 1; i <= m_nNumber; i++)
	{
		if (m_pCount[i])
		{
			fprintf(fp, "%d %d", i, m_pCount[i]);
		}
	}

	fclose(fp);
}

int _tmain(int argc, _TCHAR* argv[])
{
	char sinput[10];
	char sfilename[FILENAMELENGTH] = "C:\\Users\\sony\\Desktop\\k\\practice\\beibaoproblem\\beibaoproblem\\input.txt";

	scanf_s("%s", sinput, _countof(sinput));

	while (_stricmp(sinput, "q") != 0)
	{
		if (_stricmp(sinput, "i") == 0)
		{
			_tprintf(_T(" please input a filename:"));
			/*scanf_s("%s", sfilename);*/

			//获取满足最大载重量的最大价值
			CBeibao beibao(sfilename);

			int nMaxValue = beibao.GetMaxValue();
			if (nMaxValue)
			{
				beibao.Display(nMaxValue);
				int nlen = strlen(sfilename);
				//这里sfilename表示头指针，sttrcpy表示复制到sfilename + nlen - 4
				strcpy_s(sfilename + nlen - 4, FILENAMELENGTH , "_result.txt");
				beibao.Display(nMaxValue, sfilename);

			}
			else
			{
				_tprintf(_T("error!"));
			}
		}

		_tprintf(_T("input command: "));
		scanf_s("%s", sinput);

	}
	

	return 0;
}

参考链接：http://blog.csdn.net/livelylittlefish/article/details/2186206

                    http://www.cnblogs.com/usa007lhy/archive/2013/05/19/3087195.html