A summary of dropout technique

1/ Motivation:

Typically, for overcoming overfitting, we introduce methods like stopping training as soon as performance on a validation set starts to get worse; soft weight sharing[2] and regularizations[1]. 

Conventionally, regularization techniques include L0/L1 and L2 regularizations and average all the possible settings of the parameters[3]. The main idea of average mean is to give each setting of parameters with the a weight which equals to posterior possibility(comes from training data) of it(the particular setting). The weighted means of each parameter will be the result of regularization. However, when the model becomes complex and big, the computation of this mean will be too large; therefore, Hinton proposed a new mean to simulate the average effect by dropout some units in the neural network. He wrote and I quoted that what he did is to 'approximating an equally weighted geometric mean of the predictions of an exponential number(2^n) of learned models that share parameters'. 

2/ How to perform dropout:

In a particular fore-propagation and back-propagation(a training case), we let some units of the network 'disappear' with their incoming nets and outgoing nets. The back-propagation here is mini-batch back-propagation. What is mini-batch propagation? You can watch my another blog: http://blog.csdn.net/firehotest/article/details/50541136

In each training case, we perform once stochastic gradient calculation for each θ. Then in a mini-batch, we calculate the average gradient of each θ. 

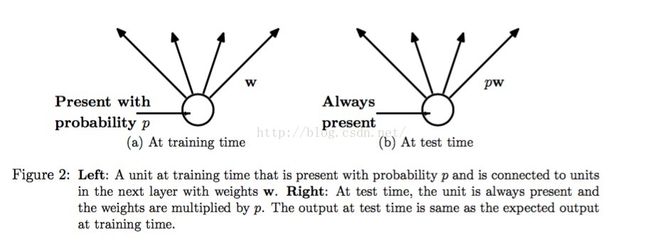
During the testing time, every incoming and outgoing weight net from a node is cross with the p(possibility) the node. 

Here is the proposed way of the paper of pre-training, training and testing the network:

1)  Using unsupervised pre-train to pre-train the network instead of random initialization.

2)  Use a labeled training set to perform supervised training. Set a mini-batch number to perform a mini-batch gradient descent. Notice here that each back-propagation of a training case uses different network, because there are nodes which have possibility of p to disappear. 

3) In the testing time, we used the whole network with the trained parameters get from 2 to perform test. However, the parameters are multiple with p. 

There is a good figure in [1] well illustrates this step 2 and 3:

 

3/ The principle of dropout and the result analysis from the paper: 

The main principle of dropout is to avoid co-adaption of units by making some units disappear during each training case. If all the units exists within each training case, it will be easy to let the units be in complex co-adaptions. 

###

About the principle of co-adaption, hinton said and I quoted: 

In a standard neural network, the derivative received by each parameter tells it how it should change so the final loss function is reduced, given what all other units are doing. Therefore, units may change in a way that they fix up the mistakes of the other units. This may lead to complex co-adaptations.

###

Here is a comparation of first hidden layer's output with and without dropout [1]: 

We can see that the units in left images have more 'details' than the units of right images. And this 'details' are the things that we do not need they learn. 

The article also presents a comparation of sparsity between network trained with or without dropout[1]. 

As we known,  a sparse network will have the better ability of anti-disturb and less opportunity of overfitting. Since the decision boundary will be more smooth than the not-sparse one. In a good sparse model, there are a few high activations for any testing data. And the average activation of units should be low.[1] 

4/ Dropout tuning

(1) The article performs two kinds of test. The first one is to keep the number of hidden units constant. The other is to keep p*n constant. 

Here is the result: 

Combine the result of two, hinton drew a conclusion that p = 0.5 will be the optimal point. 

(2) Change the activation function of units

There are three kinds of activation function could be used in dropout. 

Sigmoid(Logistic)

ReLu(Rectified Linear Units)

Maxout

As the sequence I listed above, the optimization direction is Logistic -> ReLu -> Maxout. 

Something beside the main part: 

'argmin' means that calculate the variable's value that makes the function's value minimum. 

 Reference:

[1] N.Srivastava G.Hinton  'Dropout: A Simple Way to Prevent Neural Networks from Overfitting' 2013

[2] S. J. Nowlan and G. E. Hinton. Simplifying neural networks by soft weight-sharing. NeuralComputation, 4(4), 1992. 

[3] http://blog.csdn.net/zouxy09/article/details/24971995