2015-2016 下半学期 第二周 训练
1、hdu4081
题意:有n个城市,秦始皇要修用n-1条路把它们连起来,要求从任一点出发,都可以到达其它的任意点。秦始皇希望这所有n-1条路长度之和最短。然后徐福突然有冒出来,说是他有魔法,可以不用人力、财力就变出其中任意一条路出来。秦始皇希望徐福能把要修的n-1条路中最长的那条变出来,但是徐福希望能把要求的人力数量最多的那条变出来。对于每条路所需要的人力,是指这条路连接的两个城市的人数之和。最终,秦始皇给出了一个公式,A/B,A是指要徐福用魔法变出的那条路所需人力, B是指除了徐福变出来的那条之外的所有n-2条路径长度之和,选使得A/B值最大的那条。
题解:首先看到A/B这个式子,发现是没法贪心的,因为A和B是有联系的,那么让A/B尽可能大就只能让B尽可能小。所以我们做一颗最小生成树,然后枚举树上的边,答案即为MAX(cost[i]+cost[j]/MST-path[i][j])。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<map>
#include<ctime>
#include<bitset>
#define LL long long
#define db double
#define EPS 1e-15
#define inf 1e8
using namespace std;
double g[1010][1010],dis[1010],maxw[1010][1010];
bool vis[1010],used[1010][1010];
int pre[1010];
struct City{
int x,y,w;
}city[1010];
db dist(City a,City b){
return sqrt(abs((a.x-b.x)*(a.x-b.x))+abs((a.y-b.y)*(a.y-b.y)));
}
int main(){
int T;
scanf("%d",&T);
while (T--){
int n;
scanf("%d",&n);
for (int i=0;i<n;i++){
scanf("%d%d%d",&city[i].x,&city[i].y,&city[i].w);
for (int j=0;j<i;j++)
g[i][j]=g[j][i]=dist(city[i],city[j]);
}
for (int i=0;i<n;i++){
dis[i]=g[pre[i]=0][i];
maxw[0][i]=0;
}
memset(vis,0,sizeof(vis));
memset(used,0,sizeof(used));
memset(maxw,0,sizeof(maxw));
vis[0]=1;
dis[n]=inf;
db mst=0.0;
for(int k=1;k<n;k++){
int x=n;
for (int i=0;i<n;i++)
if (!vis[i] && dis[i]<dis[x]) x=i;
for (int i=0;i<n;i++)
if (vis[i]) maxw[i][x]=maxw[x][i]=max(dis[x],maxw[i][pre[x]]);
mst+=dis[x];
vis[x]=true;
used[x][pre[x]]=used[pre[x]][x]=true;
for (int i=0;i<n;i++)
if (!vis[i] && g[x][i]<dis[i]) dis[i]=g[pre[i]=x][i];
}
db ans=0;
for (int i=0;i<n;i++)
for (int j=0;j<i;j++)
ans=max(ans,(city[i].w+city[j].w)/(mst-maxw[i][j]));
printf("%.2f\n",ans);
}
return 0;
}
2、poj1062
题意:中文题。
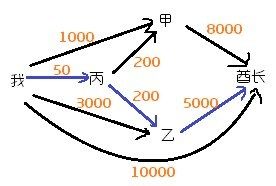
题解:这个题非常容易看成一张有向图,人是图中的节点,边权为需要附加的金钱,比如样例,我们可以把它画成下面的图。
那么剩下的等级问题,我们可以通过枚举等级区间[l-m,m]~[m,l+m]中的点来解决,不在这个区间内的点在最短路的状态被标记为已访问,这样就不会出现错误。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<map>
#include<ctime>
#include<bitset>
#define LL long long
#define db double
#define EPS 1e-15
#define inf 1e8
using namespace std;
int dijkstra(int n, int mp[][101], int vis[]){
int dis[101]={0},minn,t;
for(int i=1;i<=n;i++) dis[i]=mp[0][i];
while(1){
minn=inf;
for(int i=1;i<=n;i++)
if ((vis[i]==0)&&(dis[i]<minn)){
minn=dis[i];
t=i;
}
if (minn==inf) break;
vis[t]=1;
for(int i=1;i<=n;i++)
if((!vis[i])&&(mp[t][i]!=inf)&&(dis[i]>dis[t]+mp[t][i]))
dis[i]=dis[t]+mp[t][i];
}
return dis[1];
}
int main(){
int m,n,l[101],x,t,v,mp[101][101],vis[101],ans=inf;
scanf("%d%d",&m,&n);
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++) mp[i][j]=inf;
for(int i=1;i<=n;i++){
scanf("%d%d%d",&mp[0][i],&l[i],&x);
for(int j=0;j<x;j++){
scanf("%d%d",&t,&v);
mp[t][i]=v;
}
}
l[0]=l[1];
for (int i=l[1]-m;i<=l[1];i++){
vis[0]=1;
for(int j=1;j<=n;j++)
if ((l[j]>=i)&&(l[j]<=(i+m))) vis[j]=0;
else vis[j]=1;
ans=min(ans,dijkstra(n,mp,vis));
}
printf("%d\n",ans);
return 0;
}
3、hdu5137
题意:从2~n-1这几个点中任意去掉一个点,使得从1到n的最短路径最大,如果任意去掉一个点1~n无通路输出Inf。
题解:枚举删除哪个点,每次在floyd数组中记录一下最短路径就好了。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<map>
#include<ctime>
#include<bitset>
#define LL long long
#define db double
#define EPS 1e-15
#define inf 1e8
using namespace std;
int n,m;
int d[40][40],g[40][40];
int solve(int x){
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
if (i==x || j==x) g[i][j]=inf;
else g[i][j]=d[i][j];
for (int k=1;k<=n;k++)
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
return g[1][n];
}
int main(){
while (scanf("%d%d",&n,&m) && (n!=0)){
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
d[i][j]=(i==j)?0:inf;
for (int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
d[u][v]=min(d[u][v],w);
d[v][u]=d[u][v];
}
int ans=0;
for (int i=2;i<n;i++)
ans=max(ans,solve(i));
if (ans==inf) puts("Inf");
else printf("%d\n",ans);
}
return 0;
}
4、hdu5025
题意:反正就一个要你满足各种条件然后到达终点的搜索题。
题解:感觉和上周那个搜索题差不多的思路,但是这次要用四维数组f[i][j][k][state]表示状态 ,f[i][j][k][state]为坐标位置走到坐标i,j时已经取得了k种钥匙,当前蛇的状态为state,然后用个优先队列维护个到达每个点用的步数。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<map>
#include<ctime>
#include<bitset>
#define LL long long
#define db double
#define EPS 1e-15
#define inf 1e8
using namespace std;
const int maxn=105;
const int dir[4][2]={{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
char mp[maxn][maxn];
int N, M;
int ok[maxn][maxn];
bool vis[maxn][maxn][10][1<<5];
struct Node{
int x,y,d,key,kill;
Node(int x, int y, int d, int key, int kill):x(x), y(y), d(d), key(key), kill(kill) {}
bool operator < (const Node & rhs) const {
return d > rhs.d;
}
};
inline bool judge(int x, int y) {
return x>=0 && x<N && y>=0 && y<N && mp[x][y]!='#';
}
int bfs(int x,int y){
memset(vis,0,sizeof(vis));
vis[x][y][0][0]=1;
priority_queue<Node> q;
q.push(Node(x,y,0,0,0));
while (!q.empty()){
Node tmp=q.top();
q.pop();
for (int i=0;i<4;i++){
Node v(tmp.x+dir[i][0],tmp.y+dir[i][1],tmp.d+1,tmp.key,tmp.kill);
if (!judge(v.x,v.y) || vis[v.x][v.y][v.key][v.kill])
continue;
vis[v.x][v.y][v.key][v.kill]=1;
if (mp[v.x][v.y]=='S'){
if(!(v.kill & (1<<ok[v.x][v.y]))){
v.d+=1;
v.kill|=(1<<ok[v.x][v.y]);
}
q.push(v);
}
else if (v.key+1==mp[v.x][v.y]-'0'){
v.key+=1;
q.push(v);
}
else if (mp[v.x][v.y]=='T' && v.key==M)
return v.d;
else q.push(v);
}
}
return -1;
}
int main(){
while (~scanf("%d%d",&N,&M),N!=0){
int cnt=0,x,y;
memset(ok,0,sizeof(ok));
for (int i=0;i<N;i++){
scanf("%s",mp[i]);
for (int j=0;j<N;j++){
if (mp[i][j]=='S') ok[i][j]=cnt++;
if (mp[i][j]=='K') x=i,y=j;
}
}
int b=bfs(x,y);
if (b==-1) puts("impossible");
else printf("%d\n",b);
}
return 0;
}