带权并查集 POJ1988 POJ2492
单纯的并查集很简单,带权并查集还能解决更多的问题,才更好玩,来个题热身。对于下面的知识,现在就当你已经熟练掌握了递归和并查集的路径压缩。
POJ1988:题目链接 http://poj.org/problem?id=1988
题目大意:有N(N<=30,000)堆方块,开始每堆都是一个方块。方块编号1 – N. 有两种操作:
M x y : 表示把方块x所在的堆,拿起来叠放到y所在的堆上。
C x : 问方块x下面有多少个方块。
操作最多有 P (P<=100,000)次。对每次C操作,输出结果。
并查集里par数组是必不可少的,然后再通过维护一些别的信息即为路径加上权值来解决更复杂的问题。
对于此题,除了par数组,还要开设
sum数组:记录每堆一共有多少方块。 若parent[a] = a, 则sum[a]表示a所在的堆的方块数目。
under数组, under[i]表示第i个方块下面有多少个方块。 under数组在 堆合并和 路径压缩的时候都要更新。
先看初始化:
void Init(){
for(int i=0;i<maxn;i++){
par[i]=i;
under[i]=0;
sum[i]=1;
}
}
重点就在under数组的更新,在路径压缩时更新应弄明白下面这点:
当前木块x下面应该有多少?应该是under[x](这是目前x所在堆中,x下面的木块个数),再加上x当前所在堆的根节点(即par[x])的under值,当然我们都知道根节点下面是没有木块的,under=0,但是在我们把x所在堆放到另一堆上之后,那么x所在堆的根节点(即par[x])的下面不就有木块了吗,那under值就不是0了。 因此,只要路径压缩时,对于当前木块x,其所在堆根节点的under值under[par[x]]是正确的,那么更新出的under[x]就是正确的。
在合并时更新: 这时更新很简单明显,把u所在堆全部放在v所在堆上,那么u下面的增加的木块个数就是v所在堆里木块的总数sum
再看路径压缩的查找:
/*注意这里,under[x]本来是从x往下到par[x]一共有多少个,那如果再加上
par[x]下面的个数,under[x]就更新正确了。我不管par[x]下面有多少,反正
路径压缩会使在执行这句话的时候让under[par[x]]保证是正确值。。
至于上面的y,它是层层递归得到的,很明显是路径压缩之后最终的根,所以
y只是用来par[x]=y,即把沿路遇到的点全部压缩到最终根(即真正的路径压缩)
这和更新under值没有半毛钱关系*/
int Find(int x){
if(x==par[x]) return x;
int y=Find(par[x]);
under[x]+=under[par[x]];
return par[x]=y;
}
可以看出under的更新是: 先一直递归到该堆的最终根,然后从最终根向x的方向一步一步更新的,"由最终根能把under[par[x]]更新正确",那么under[x]自然就正确,那么x的子孙(即par[a]=x的a)也就能更新正确。
合并:
//在路径压缩完成后,就可以把u和v分别看出一个整体,
//如果把u放在v上面,自然v里的全部砖块都要算到under[x]里
void Union(int u,int v){
if((u=Find(u))==(v=Find(v)))
return ;
under[u]+=sum[v];
par[u]=v;sum[v]+=sum[u];
}AC代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int maxn=30000+10;
int sum[maxn],par[maxn],under[maxn];
void Init(){
for(int i=0;i<maxn;i++){
par[i]=i;
under[i]=0;
sum[i]=1;
}
}
//注意这里,under[x]本来是从x往下到par[x]一共有多少个,那如果再加上
//par[x]下面的个数,under[x]就更新正确了。我不管par[x]下面有多少,
//反正路径压缩会使在执行这句话的时候让under[par[x]]保证是正确值。。
//至于上面的y,它是层层递归得到的,很明显是路径压缩之后最终的根,所以
//y只是用来par[x]=y,即把沿路遇到的点全部压缩到最终根(即真正的路径压缩)
//这和更新under没有半毛钱关系
int Find(int x){
if(x==par[x]) return x;
int y=Find(par[x]);
under[x]+=under[par[x]];
return par[x]=y;
}
//在路径压缩完成后,就可以把u和v分别看出一个整体,
//如果把u放在v上面,自然v里的全部砖块都要算到under[x]里
void Union(int u,int v){
if((u=Find(u))==(v=Find(v)))
return ;
under[u]+=sum[v];
par[u]=v;sum[v]+=sum[u];
}
int main()
{
int i,j,p;
char s[5];
Init();
scanf("%d",&p);
while(p--){
scanf("%s",s);
if(s[0]=='M'){
int a,b;
scanf("%d%d",&a,&b);
Union(a,b);
}else {
int x;
scanf("%d",&x);
Find(x); //要先压缩一下,然后再查询
printf("%d\n",under[x]);
}
}
return 0;
}
Find函数完成路径压缩和信息更新的"四步曲":
①par[x]==x递归出口 ②一直递归找最终根并记录到y ③更新当前节点和父亲节点信息 ④返回par[x]=y,完成路径压缩。
在带权并查集中我们维护的信息一般都是当前节点x和其直接父亲par[x]的关系,所以在第三步时用par[x]的信息来更新x的信息。
下面再来看一个更直观的例子。
POJ2492 题目链接:http://poj.org/problem?id=2492
题目大意:共n个虫子,编号1-n,给出m个关系,用x,y描述,含义是:x和y有好感。问这m个关系给出后,是否能判断出有某一对虫子是同性恋,yes or no。
上面说过,在带权并查集里我们一般是维护当前节点x与其父亲的关系,在这看本题,应该会想到我们要维护什么样的信息,那就是: 用一个rel[]数组,来维护x和par[x]的性别关系,rel[x]=0表示x和par[x]是同性,rex[x]=1表示是异性,所以我们在维护并查集时还要维护这个rel信息。
先看初始化:
void Init(int n){
for(int i=0;i<=n;i++){
par[i]=i,rel[i]=0;
}
}一开始每个虫子都和自己是同性,能理解。
在Find函数路径压缩时,rel[]又该怎么更新呢?
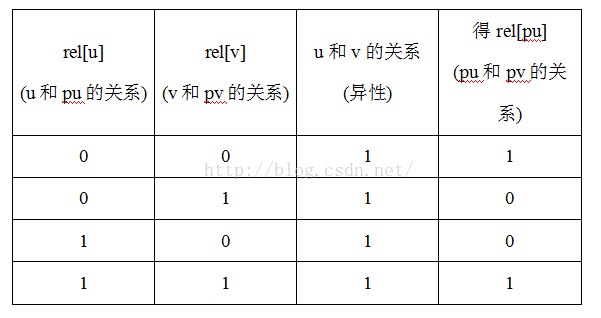
我们先看我们的目的:因为我们这是路劲压缩,即把所有经过的节点的par都指向最终根(设为y),所以在Find(x)时,最终rel[x]表示的是x和y的性别关系(当然最终par[x]会等于y,符合rel[]的定义)。由上面蓝色的话,我们可以知道,Find函数中,par[x]的rel[]是确定的(不要问为什么,上面已经说的很清楚了,看蓝色字的""号部分),因此,我们现在我们就是已知x和par[x]的关系,par[x]和y的关系,求x和y的关系,很简单吧。列个表给看一下。
这个表自己好好体会,然后一想一划就能明白。
我们可以看出新的rel[x]可以由之前的rel[x]和rel[par[x]],且等于rel[x]^rel[par[x]]。 我们的目的就达到了。
再看代码:
int Find(int x){
if(x==par[x]) return x;
int y=Find(par[x]);
rel[x]=rel[x]^rel[par[x]];
return par[x]=y;
}四步曲还是一样。这样就维护了rel[x]。
对于给出的一对虫子,怎么判断他们是不是同性的呢?
这就看Union合并函数了,先帖代码,接着分析。
bool Union(int u,int v){ //返回true:同性;否则异性
int pu=Find(u),pv=Find(v);
if(pu==pv) return rel[u]==rel[v]; //如果在同一个集合里,那么两者与祖先的性别关系一样的话说明两者同性
rel[pv]=!(rel[u]^rel[v]);
par[pv]=pu;
return false;
}注意Union函数的返回值含义。
设pu=Find(u),pv=Find(v),对于给定的一对虫子u和v,有两种情况:
1.两者在同一集合里,pu==pv:那就好办了,也不能合并,而且能一下就能判断出两者的性别关系,他们的rel[]都是相对于同一根节点的,如果你和你爸是同性,我和你爸是同性,那么咱俩的性别关系不就是同性吗。
2.两者不在同一集合里,pu!=pv: 那么u,v的关系我们就认为是异性,并以此为据来合并两个集合,合并两个集合就是其实就是合并pu和pv啊,我们就把以pu为根的集合合并到以pv为根的集合,即par[pu]=pv,但是我们还要更新rel[pu],即pu和pv的关系,他们的关系怎么确定呢? 首先我们知道u和pu的关系为rel[u],v和pv的关系为rel[v],且我们还要保证u和v异性,由这三个关系就能确定pu和pv的关系!!列个表看一下:
那第一个简单说明一个,u和pu是同性,v和pv也是同性,u和v是异性,则pu和pv自然是异性。
因此rel[pu]=!(rel[u]^rel[v])。
大概就是这么多。
AC代码:
/*
带权并查集
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int maxn=2000+10;
typedef struct WUFSet{
int par[maxn],rel[maxn]; //0同性,1异性
void init(int n){
for(int i=0;i<=n;i++){
par[i]=i;rel[i]=0;
}
}
int Find(int x){
if(x==par[x]) return x;
int y=Find(par[x]);
rel[x]=rel[x]^rel[par[x]];
return par[x]=y;
}
bool Union(int u,int v){ //返回true:同性;否则异性
int pu=Find(u),pv=Find(v);
if(pu==pv) return rel[u]==rel[v]; //如果在同一个集合里,那么两者与祖先的性别关系一样的话说明两者同性
rel[pv]=!(rel[u]^rel[v]);
par[pv]=pu;
return false;
}
}WUFSet;
int main()
{
int i,T,n,m,kcase=1;
WUFSet s;
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
s.init(n);
bool yes=true;
while(m--){
int a,b;
scanf("%d%d",&a,&b);
if(s.Union(a,b))
yes=false;
}
printf("Scenario #%d:\n",kcase++);
if(yes)
printf("No suspicious bugs found!\n\n");
else
printf("Suspicious bugs found!\n\n");
}
return 0;
}