单链表应用--一元多项式求和
用带头结点的单链表 设两个工作指针p和q,分别指向两个单链表的开始节点,两个多项式求和的实质上是对结点p的指数域和结点q的指数域进行比较。分三种情况
(1)若p->exp<q->exp,则结点p应为结果中的一个结点,将指针p后移。
(2)若p->exp>q->exp,则结点q应为结果中的一个结点,将q插入到第一个单链表结点p之前,再将指针q后移。
(3)若p->exp=q->exp,则p与q所指的为同类项,将q的系数加到p的系数上,若相加结果不为0,则将指针p后移,删除结点q,若相加结果为0,则标明结果中无此项,删除结点p和结点q,并将指针p和指针q分别后移。
template<typename T>
void add(linklist<T> &A,linklist<T> B){
node<T>*pre=A.first;
node<T>*p=pre->next;
node<T>*qre=B.first;
node<T>*q=qre->next;
//qre,pre始终是q,p的前驱节点
while(q&&p){
if(p->exp<q->exp){pre=p;p=p->next;}//第一种情况
else if(p->exp>q->exp){
node<T>*t=q->next;
pre->next=q;
q->next=p;
qre->next=t;
q=t;}//第二情况,q插入p之前
else {
p->data=p->data+q->data;
if(p->data==0){
pre->next=p->next;
delete p;
p=pre->next;}
else {pre=p;
p=p->next;}
qre->next=q->next;//删除节点q
delete q;
q=qre->next;}//第三种
}
if(q)pre->next=q;
}例如:x+5x^3+x^4
x^2+6x^3-x^4
其和为x+x^2+11x^3
调用:
#include<iostream>
#include<cstdlib>
#include<string>
using namespace std;
//link list
struct ele{
int data;
int exp;};
template<typename T>
struct node{
T data;
T exp;
node<T>*next;};
template<typename T>
class linklist{
private:node<T>*first;//单链表的头指针
int linksize;
public:
linklist(){fisrt=new node<T>;
first->next=NULL;//无参构造构造空线性表
linksize=0;}
linklist(ele A[],int m){
first=new node<T>;
linksize=m;
node<T>*p=first;
for(int i=0;i<m;i++){
node<T>*s=new node<T>;
s->data=A[i].data;
s->exp=A[i].exp;
p->next=s;
p=s;}
p->next=NULL;}
~linklist(){
node<T>*p=first;
while(p){
node<T>*q=p;
p=p->next;
delete q;}}
int size();
T get(int i);
int loc(T x);
void insert(int i,T x);
T del(int i);
void prt();
template<typename T>
friend void add(linklist<T> &A,linklist<T> B);};//友元函数,可以直接使用类私有数据first
template<typename T>
int linklist<T>::size(){
return linksize;}
template<typename T>
T linklist<T>::get(int i){
node<T>*p=first;
int j=0;
while(p&&j<i){
p=p->next;
j++;}
if(!p) throw"i error";
else return p->data;}
template<typename T>
int linklist<T>::loc(T x){
node<T>*p=first;
int j=0;
while(p&&x!=p->data){
p=p->next;
j++;}
if(!p)throw"x no";
else return j;}
template<typename T>
void linklist<T>::insert(int i,T x){
node<T>*p=first;
int j=0;
while(p&&j<i-1){
p=p->next;
j++;}//找到i-1
if(!p)throw"insert error";
else{
node<T>*s=new node<T>;
s->data=x;
s->next=p->next;
p->next=s;}
linksize++;}
template<typename T>
T linklist<T>::del(int i){
node<T>*p=first;
int j=0;
while(p&&j<i-1){
p=p->next;
j++;}
if(!p||!p->next)throw"del error";
else{
T t=p->next->data;
p->next=p->next->next;
return t;}
linksize--;}
template<typename T>
void linklist<T>::prt(){
node<T>*p=first;
if(!p)cout<<"empty"<<endl;
p=p->next;
while(p){
cout<<p->data<<" and "<<p->exp<<" ";
p=p->next;}
cout<<endl;}
template<typename T>
void add(linklist<T> &A,linklist<T> B){
node<T>*pre=A.first;
node<T>*p=pre->next;
node<T>*qre=B.first;
node<T>*q=qre->next;
//qre,pre始终是q,p的前驱节点
while(q&&p){
if(p->exp<q->exp){pre=p;p=p->next;}
else if(p->exp>q->exp){
node<T>*t=q->next;
pre->next=q;
q->next=p;
qre->next=t;
q=t;}
else {
p->data=p->data+q->data;
if(p->data==0){
pre->next=p->next;
delete p;
p=pre->next;}
else {pre=p;
p=p->next;}
qre->next=q->next;
delete q;
q=qre->next;}
}
if(q)pre->next=q;
}
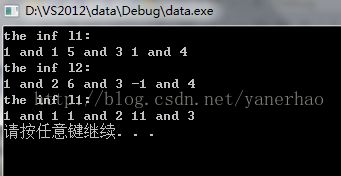
int main(){
ele A[]={{1,1},{5,3},{1,4}};
ele B[]={{1,2},{6,3},{-1,4}};
linklist<int>l1(A,3);
linklist<int>l2(B,3);
cout<<"the inf l1:"<<endl;
l1.prt();
cout<<"the inf l2:"<<endl;
l2.prt();
add(l1,l2);
cout<<"the inf l1:"<<endl;
l1.prt();
system("pause");
return 0;
}