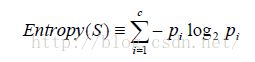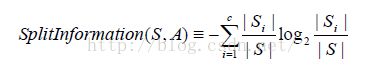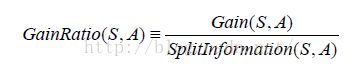机器学习：决策树ID3\C4.5\CART\随机森林总结及python上的实现 (2)

本文主要根据Mitchell的机器学习总结归纳，图片大多来源于此，同时结合网上搜索到的资料和几篇较新的文献，自己写的决策树总结，当中的python算法摘自《集体智慧编程》，算法可在python2.7环境下运行。（本来想自己写的。。可是不懂数据结构的树，写的太不像样了，所以就看完智慧编程自己盲打了一遍，顺便了解了下树这种数据结构）

首先：

# define 结点 节点  //咳咳，本文中的所有'结点'的正确写法都是'节点'，懒得改了 =_= 大家应该懂的。。。

决策树是目前应用最广的归纳推理算法之一，属于归纳学习的一种。主要用于分类离散值，不过改进后的算法也能对连续型数值进行分类。决策树对噪声具有很好的鲁棒性，常见的决策树算法形式主要有ID3，C4.5，CART等。

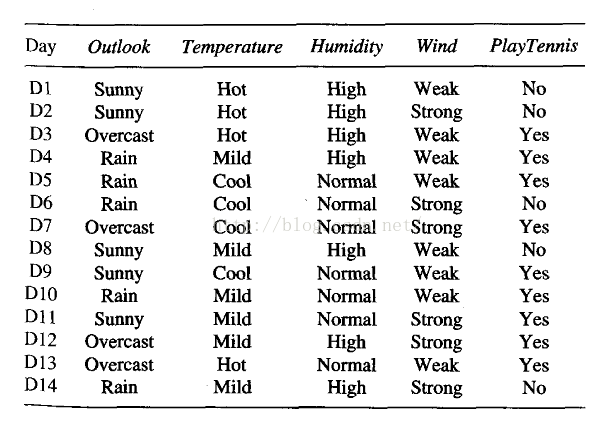
考虑训练数据如下：

其决策树形式如下：

如图：从上到下，把样本从最上的根节点排列到最后的叶子节点，叶子节点的值即代表了样本所属的分类。每个方框节点代表了样本的属性，其下的各个分叉线上的字母即为该属性的各个可能值，不断向下分叉直到分完所有训练数据。

接下里说下决策树用的算法。

一、决策树常见算法

ID3

ID3是最简单的决策树形式。回顾上面的决策树形式，你应该会发现一个疑点，那就是为什么我们选取了outlook作为根节点，而不选用其他的，或者说其实选哪个根节点都没事呢？

这就涉及到一个概念，那就是最优分类属性。算法判断outlook是最优分类属性，他能使得这个决策树长的最简单。

最优分类属性是通过信息增益比率来判断的。介绍前先引入一个概念，叫信息熵。如下：

如公式，S表示训练数据集合，i=1→c是目标概念可能的取值，如上面就是两个no和yes，Pi表示属于目标概念i的训练数据个数占S的比率。

信息熵是从热力学的熵中引申来的，我们知道在热力学中，熵表示的是一种无序状态，即越无序熵越大，有序结构的熵为0。而信息熵表示，一个东西他的不确定性越高，他的熵就越大，当他完全确定时，他的信息熵为0。

举个例子：

(前提：我们假设天气预报给出的预测概率是绝对正确的。)

天气预报说明天100%会下雨，好的那这句话所对应的信息熵就是 -1*log1=0，

天气预报说明天50%的可能会下雨，50%的可能会是晴天，那他的信息熵就是-0.5*log0.5-0.5*log0.5=1，

天气预报说明天25%可能下雨，25%可能晴天，50%可能阴天，那么可以计算其信息熵为1.5

从这个例子可以看出，当事物的不确定性上升的时候，他的信息熵会变大。

然后给出信息增益的定义：

公式中的第二项是S按照属性A进行分类后，整体所具有的信息熵。value(A)表示A中具有的所有属性的值，计算各个属性值下的信息熵Sv在乘上Sv所含的样本数比例，相加得到按A分类后的信息熵。两者相减即为信息增益Gain(S,A)。

在这里还是举个例子：

计算最上面的表格Enjoysport按属性wind划分后的信息增益如下：

然后说下我们为什么要引入信息增益的概念。从信息增益的公式就可以看出，当第二项的值很小的时候，即按照A属性划分后，整体的熵很小时，信息增益就会很大，这个时候我们说，按照A属性来进行划分，使得整体熵显著变小了！信息增益就表示了按照属性A划分后整体熵的降低值。最开始的最优分类属性便是采取信息增益来度量，将最大的选为最优的分类属性，之后每层都是如此，每次都选取最优的属性，但是这种方法存在一个很严重的问题，即当一个属性的值过多且没有实际分类价值时，他的信息增益会特别大，使得决策树成为一个深度为1，但是宽度很大的决策树，如日期属性年月日，如果将其划入分类的话，最后会生成根节点为日期，深度为一的决策树，但是这个决策树的分类效果极其之差，当在验证数据上进行验证时，他几乎无法进行分类。

所以我们定义信息增益比率来避免这种情况，如下：

公式中Si跟信息增益中的Si意思一样，仍是属于i的样例个数。当属性的分类过多时，他的splitInformation会变大，以此来平衡。但是他也存在一个问题：即，当S中某个分类Si的样例过多，其他属性值下分类过少时，即Si→S时，会使得Split→0，所以最后大家想了一个折中的办法：先依次计算所有属性的Gain，然后仅对那些Gain值超过平均值的计算GainRatio。

好了，总算扯完信息增益比率了。。所以最后的结论就是ID3运用Gain自上而下选取每个最优属性作为节点进行分类。而后面说到的Gainratio其实是C4.5所使用的了。

C4.5

C4.5其实就是ID3的扩展，最简单的决策树形式用来处理离散值输入和输出，于是人们扩展了决策树的功能，并加入了其他的扩展，衍生出了C4,5。C 4.5比ID3多了一些特性：

1、可用于对连续型输入或输出进行拟合。虽说如此，其实也只是把连续的值划分为几个区间来输入而已。

2、可处理缺少某些属性的数据。收集的数据常常会有某些属性值是缺失的，就像医院里统计的病人的各种检测数据，总会有A做了抽血化验没有尿检，B做了尿检却没有抽血化验。这个时候信息增益就很难计算，所以我们会主动给这些数据“补上”缺失的属性。一般有三种方法：①赋给他结点n下的训练样例中该属性的最常见值②赋给他结点n下被分类为他所属的类里该属性的最常见值。③按照概率划分。按照结点n下该属性在已知数据中出现的概率划分给其他未知的实例。

3、增加了对过度拟合的处理：错误率后修剪法和规则后修剪法。矫正过度拟合最常采用验证集合来调整。①错误率后修剪法：对生成的决策树自下而上，每次删除一个节点，然后在验证集合上进行验证，如果修剪后的决策树在验证集合上得到了更小的错误率，那就说明这次修剪是有效的，剔除那个节点，否则决策树不变，知道判断完所有节点。②规则后修剪：将各个节点表示成if-then的规则化表示再进行修剪。如上面提到的那棵决策树，最左一条支路用规则来表示可以写成：iIF (Outlook=sunny) and (Humidity=high) ,THEN PlayTennis=No，像这样将所有的支路表示成规则后，每次剔除一个规则就统计在验证集合上的错误率情况，直到得到最优的决策树。

一般来说第二种方法较常采用，因为规则化后的形式比较有利于人的理解，而且每次剔除的规则只是某个属性的一个值，但是第一种方法却剔除了一个属性下的所有属性值，这是不太好的。

4、处理代价不同的属性：某些属性不好采集，或者属性的采集需要付出很高的成本代价(人力或者金钱)时，我们通常只在需要可靠分类时才统计他们，当不需要时会尽量选用代价低的属性来进行决策树的生成。如下：

会使低代价的属性被优先选取。

CART(classification and regression tree)

cart是一种二分递归分割树。他每个结点下只有两个属性值(当一个属性含有三个以上属性值时，我们人为的把他分为两类如：A和非A)，

所以最后他会生成一个很规则的二叉树。

ID3和C4.5的分类基础都是采用的信息熵衍生而来的信息增益，而cart使用的是基尼不纯度(Gini impurity)

Gini在分类类别越杂乱的时候越大，类似于信息熵。其定义如下：

当采用Gini来选取最优分类属性时，我们按照下面的计算公式来：

公式里，value(A)代表A属性里所有可能的取值，pi表示value(A)里各个分类的比率，分别计算他的Gini指数，Sa代表属性A取a值时的实例个数，SA为A属性里的总实例个数，其实就是整个训练数据个数。

同样举个例子如下：计算上表中按照Wind分类的Gini_gain

其中

Wind=strong有6个实例，其中3个No，3个Yes，wind=weak有8个实例，其中2个No，6个Yes。

	Strong	Weak
No	3	2
Yes	3	6

Gini(Strong)=1-(3/6)^2-(3/6)^2=0.5

Gini(Weak)=1-(2/8)^2-(6/8)^2=0.375

Gini_gain(Wind)=(6/14)*0.5+(8/14)*0.375

以上，最后也是选取Gini_gain最大的为根节点，跟信息增益其实是类似的。

PS：注意这里是CART二分递归，所以如果计算Outlook时，前期已经将数据划分为overcast和非overcast了。

随机森林

随机森林（RandomForest）并不是独立于ID3，C4.5，cart之外的算法，他结合了数学上的随机抽样，运用自助法(boot-strap)重采样，来达到一种更好的拟合。下面介绍自助法中的bagging模式，步骤如下：

①假设目前训练数据D有N个实例，M个特征，我们采用放回抽样抽出n个数据，m个特征组成一个训练数据D1，再用同样的方法抽出n、m组成D2，然后D3......Dn

②分别用这n组训练数据，如采用C4.5分别生成一个决策树。

③将每个决策树的决策汇总，选择当中占比最高的决策作为整个森林的决策结果。（这种方法使用最多）

或

③用验证集合对n个决策树进行投票，选中表现最好的决策树。(投票的意思应该是看谁在验证集合上分类出错率最小)

另一种自助法采用模式是Adaboosting，有兴趣可以百度下，他主要对每个实例分配一个概率来抽取。

由整个森林的投票来决定结果可以避免单棵树过拟合的情况，使得决策更加合理，随机森林近年来在各种数据挖掘大赛前几名中出现的频率极高，是一个很有潜力的算法。

对于第二个③，因为采用了随机抽样来生成训练数据，所以n个数据集里有很大可能出现一个不包含噪声或噪声很少的数据集Di，由他生成的决策树将在后来的投票中具有很高的票数。因此随机森林的方法对噪声有很好的鲁棒性，而且能够很大程度上避免过度拟合，因为我们总是选取在验证集合上表现最好的一棵决策树。

python的scikit-learn包里封装了随机森林，感兴趣的同学可以了解下。scikit-learn里封装了很多分类器，帮使用者节省了很多时间，scikit-learn简单到了甚至被称作了toy play工具包了。

二、目前决策树的研究进展

目前的决策树研究方向主要有两：①将决策树与其他算法相融合②寻找新的构建决策树的方法。

关于①融合，目前有决策树跟ANN(神经网络)、GA(遗传算法)等，结合了不同算法的优点，如将决策树转化成神经网络的结构，加速神经网络的运算。关于②寻找新方法，前几年提出了个CHAIN算法，不知道现在怎么样了

大家感兴趣想深入了解的话可以去看看最新的文献，哈哈

对了，关于算法的融合，不知道这个算不算，不过我再看到的时候着实惊艳了一把，当然这也是因为我现在还比较小白的原因，=_=，早几天前看了coursera上的机器学习基石，里面在提到感知器时介绍了对于分类错误之后的惩罚，如某些错误是我们无论如何都想避免的，那我们就会在这个错误出现时赋予他较高的犯错代价，以修改感知器的假设函数拟合。如：国家安全局进入需要指纹验证，用感知器来进行分类即：验证指纹合格或不合格。可能分类错误的情况有：指纹匹配但是机器提示不合格、指纹不匹配但是机器提示合格。大家一看就知道第二个错误是不能允许的，毕竟对于安全局这种地方，出现一次这样的错误成本太高了，而出现第一个错误的管理者还可以骂娘一下再验证一次。所以这里我们就会赋予第二个错误以较高的权重代价，来引导感知器。

然后这几天查文献，发现决策树里面有的也用到这个概念了！他将某些决策犯错的分类赋予了较高的代价，使得他在验证数据集上会尽量选取犯这种错误较少的决策树！当时对我的震惊是极大的，毕竟我才刚看完各种算法的介绍，谈互相之间的融合还太早，脑子转不过来，这个时候看到这个，对我的触动是极大的。算法真是博大精深啊

相信在实际的应用当中，算法之间的融合只会更多。

三、决策树的python代码实现

暂无

#!usr/bin/env python2
#-*- coding:utf-8 -*-


from math import log
from PIL import Image,ImageDraw
import zlib

my_data=[['slashdot','USA','yes',18,'None'],
['google','France','yes',23,'Premium'],
['digg','USA','yes',24,'Basic'],
['kiwitobes','France','yes',23,'Basic'],
['google','UK','no',21,'Premium'],
['(direct)','New Zealand','no',12,'None'],
['(direct)','UK','no',21,'Basic'],
['google','USA','no',24,'Premium'],
['slashdot','France','yes',19,'None'],
['digg','USA','no',18,'None'],
['google','UK','no',18,'None'],
['kiwitobes','UK','no',19,'None'],
['digg','New Zealand','yes',12,'Basic'],
['slashdot','UK','no',21,'None'],
['google','UK','yes',18,'Basic'],
['kiwitobes','France','yes',19,'Basic']]


#创建决策节点
class decidenode():
    def __init__(self,col=-1,value=None,result=None,tb=None,fb=None):
        self.col=col         #待检验的判断条件所对应的列索引值
        self.value=value     #为了使结果为true，当前列要匹配的值
        self.result=result   #叶子节点的值
        self.tb=tb           #true下的节点
        self.fb=fb           #false下的节点


#对数值型和离散型数据进行分类
def DivideSet(rows,column,value):
    splitfunction=None
    if isinstance(value,int) or isinstance(value,float):
        splitfunction=lambda x :x>=value
    else:
        splitfunction=lambda x :x==value

    set1=[row for row in rows if splitfunction(row[column])]
    set2=[row for row in rows if not splitfunction(row[column])]
    return (set1,set2)


#计算数据所包含的实例个数
def UniqueCount(rows):
    result={}
    for row in rows:
        r=row[len(row)-1]
        result.setdefault(r,0)
        result[r]+=1
    return result

#计算Gini impurity
def GiniImpurity(rows):
    total=len(rows)
    counts=uniquecounts(rows)
    imp=0
    for k1 in counts:
        p1=float(counts[k1])/total
        for k2 in counts:
            if k1==k2: continue
            p2=float(counts[k2])/total
            imp+=p1*p2
    return imp

#计算信息熵Entropy
def entropy(rows):
    log2=lambda x:log(x)/log(2)
    results=UniqueCount(rows)
    # Now calculate the entropy
    ent=0.0
    for r in results.keys( ):
        p=float(results[r])/len(rows)
        ent=ent-p*log2(p)
    return ent

#计算方差(当输出为连续型的时候，用方差来判断分类的好或坏，决策树两边分别是比较大的数和比较小的数)
#可以通过后修剪来合并叶子节点
def variance(rows):
    if len(rows)==0:return 0
    data=[row[len(rows)-1] for row in rows]
    mean=sum(data)/len(data)
    variance=sum([(d-mean)**2 for d in data])/len(data)
    return variance


###############################################################33
#创建决策树递归
def BuildTree(rows,judge=entropy):
    if len(rows)==0:return decidenode()   

    #初始化值
    best_gain=0
    best_value=None
    best_sets=None
    best_col=None   
    S=judge(rows)
    

    #获得最好的gain
    for col in range(len(rows[0])-1):
        total_value={}    
        for row in rows:
            total_value[row[col]]=1
        for value in total_value.keys():
            (set1,set2)=DivideSet(rows,col,value)

            #计算信息增益，将最好的保存下来
            s1=float(len(set1))/len(rows)   
            s2=float(len(set2))/len(rows)          
            gain=S-s1*judge(set1)-s2*judge(set2)
            if gain > best_gain:
                best_gain=gain
                best_value=value
                best_col=col
                best_sets=(set1,set2)
    #创建节点
    if best_gain>0:
        truebranch=BuildTree(best_sets[0])
        falsebranch=BuildTree(best_sets[1])
        return decidenode(col=best_col,value=best_value,tb=truebranch,fb=falsebranch)
    else:
        return decidenode(result=UniqueCount(rows))


#打印文本形式的tree
def PrintTree(tree,indent=''):
    if tree.result!=None:
        print str(tree.result)
    else:
        print '%s:%s?' % (tree.col,tree.value)
        print indent,'T->',
        PrintTree(tree.tb,indent+'  ')
        print indent,'F->',
        PrintTree(tree.fb,indent+'  ')

def getwidth(tree):
    if tree.tb==None and tree.fb==None: return 1
    return getwidth(tree.tb)+getwidth(tree.fb)


def getdepth(tree):
    if tree.tb==None and tree.fb==None: return 0
    return max(getdepth(tree.tb),getdepth(tree.fb))+1


#打印图表形式的tree
def drawtree(tree,jpeg='tree.jpg'):
    w=getwidth(tree)*100
    h=getdepth(tree)*100+120
    img=Image.new('RGB',(w,h),(255,255,255))
    draw=ImageDraw.Draw(img)
    drawnode(draw,tree,w/2,20)
    img.save(jpeg,'JPEG')


def drawnode(draw,tree,x,y):
    if tree.result==None:
    # Get the width of each branch
        w1=getwidth(tree.fb)*100
        w2=getwidth(tree.tb)*100
        # Determine the total space required by this node
        left=x-(w1+w2)/2
        right=x+(w1+w2)/2
        # Draw the condition string
        draw.text((x-20,y-10),str(tree.col)+':'+str(tree.value),(0,0,0))
        # Draw links to the branches
        draw.line((x,y,left+w1/2,y+100),fill=(255,0,0))
        draw.line((x,y,right-w2/2,y+100),fill=(255,0,0))
        # Draw the branch nodes
        drawnode(draw,tree.fb,left+w1/2,y+100)
        drawnode(draw,tree.tb,right-w2/2,y+100)
    else:
        txt=' \n'.join(['%s:%d'%v for v in tree.result.items( )])
        draw.text((x-20,y),txt,(0,0,0))



#对新实例进行查询
def classify(observation,tree):
    if tree.result!=None: return tree.result
    else:
        v=observation[tree.col]
        branch=None
        if isinstance(v,int) or isinstance(v,float):
            if v>=tree.value:
                branch=tree.tb
            else:
                branch=tree.fb
        else:
            if v==value:
                branch=tree.tb
            else:
                branch=tree.fb
        return classify(observation,branch)


#后剪枝,设定一个阈值mingain来后剪枝，当合并后熵增加的值小于原来的值，就合并
def prune(tree,mingain):
    if tree.tb.result==None:
        prune(tree.tb,mingain)
    if tree.fb.result==None:
        prune(tree.fb,mingain)

    
    if tree.tb.result!=None and tree.fb.result!=None:
        tb1,fb1=[],[]
        for v,c in tree.tb.result.items():
            tb1+=[[v]]*c    #这里是为了跟row保持一样的格式，因为UniqueCount就是对这种进行的计算

        for v,c in tree.fb.result.items():
            fb1+=[[v]]*c

        delta=entropy(tb1+fb1)-(entropy(tb1)+entropy(fb1)/2)
        if delta<mingain:
            tree.tb,tree.fb=None,None
            tree.result=UniqueCount(tb1+fb1)

#对缺失属性的数据进行查询
def mdclassify(observation,tree):
    if tree.result!=None:
        return tree.result

    if observation[tree.col]==None:
        tb,fb=mdclassify(observation,tree.tb),mdclassify(observation,tree.fb)        #这里的tr跟fr实际是这个函数返回的字典
        tbcount=sum(tb.values())
        fbcount=sum(fb.values())
        tw=float(tbcount)/(tbcount+fbcount)
        fw=float(fbcount)/(tbcount+fbcount)

        result={}
        for k,v in tb.items():
            result.setdefault(k,0)
            result[k]=v*tw
        for k,v in fb.items():
            result.setdefault(k,0)
            result[k]=v*fw
        return result

    else:
        v=observation[tree.col]
        branch=None
        if isinstance(v,int) or isinstance(v,float):
            if v>=tree.value:
                branch=tree.tb
            else:
                branch=tree.fb
        else:
            if v==tree.value:
                branch=tree.tb
            else:
                branch=tree.fb
        return mdclassify(observation,branch)



def main():                  #以下内容为我测试决策树的代码
    a=BuildTree(my_data,0.01)
    print a

    PrintTree(a)
 #   drawtree(a,jpeg='treeview.jpg')
    prune(a,0.1)
    PrintTree(a)
    prune(a,1)
    PrintTree(a)
    
    mdclassify(['google','France',None,None],a)
    print mdclassify(['google','France',None,None],a)

    mdclassify(['google',None,'yes',None],a)
    print mdclassify(['google',None,'yes',None],a)


if __name__=='__main__':
    main()

小结：

介绍了决策树的三种常见算法：基于信息熵的ID3、C4.5，基于Gini的CART，还有运用自助法的随机森林。

讲述了决策树最近的研究进展，其实这也是其他算法的前进方向，即不同算法之间的互相融合。

给出了关于某个形式的决策树实现代码，在编写代码的过程中，体会到其实最重要的环节往往在数据预处理上，如何鉴别某些变量是无关变量，对缺失属性的数据的处理，代价高昂的属性是否要收集，这些实际的问题，才是阻碍数据分析与挖掘的要点之一。