Study Note: Instruction Optimisation of CUDA programming

Consideration 1: Branch Divergence 

Before we talk about this, let us go through what is going on in GPU actually.

Here is the abstract model of SM like[1]:

Every SM has one control unit to get the instructions and interpret the instructions. Then this control unit outputs the control signal to all the SP belong to it. Every SP executes one thread in a particular warp and what they are doing are the same since the control signals are the same. Therefore, it is called a vectorised computation. Also called a SIMD pattern. 

However, if our kernel code includes data depend branch divergence (different kind of data execute different instruction), then how should the SM handle this?

For example, if we have a code of this [1]:

It turns out it does it in a stupid way: 

For all the data of array a and b, GPU will calculate all the three possible result of the given data. And construct a make based on the data condition, to mask out the results that are redundant. However, as we can image, it will waste our computation resources and 3x slower than code without branch divergent. 

Just remember that when we are talking about branch divergent, we are actually talking about branch divergent in a warp. 

Therefore, here is some way you can alleviate the side effect of branch divergent when you cannot avoid generating divergent: 

1) Decrease the computation within each branch (利用运算的结合律，把主要的运算集中在主干道，让支干负责简单的运算如赋值运算)[1]

2) Remember we only need to decrease the branch divergent in one warp. So when the if statement can distribute the branch into two warp, it will be fine. (让if语句把分支分到两个不同的warp，那个一个warp内看上去只有一个分支)

I would like to use reduction problem (归约问题) as an example.  A reduction algorithm extracts a single value from an array of values.The single value could be the sum, the maximal value, the minimal value,etc., among all elements. All of these types of reductions share the same computation structure.

For reduction problem, there are three ways to do in CUDA: 

1) The stupid way: 

A reduction can be easily achieved by sequentially going through every element of the array. When an element is visited, the action to take depends on the type of reduction being performed.For a sum reduction, the value of the element being visited at the current step, or the current value, is added to a running sum. The sequential algorithm ends when all of the elements are visited[2].

2) More advance way:

Since reduction problem are doing the same computation to each element, therefore; it can be accumulated when you can get the reduction results of different subsets and then performing reduction on these results. 

A parallel reduction algorithm typically resembles that of a soccer tournament. In fact, the elimination process of the World Cup is a reduction of “maximal,” where the maximal is defined as the team that beats all of the other teams[2]. 

So we can do the sum reduction in this way[2]: 

And here is the code to achieve this[2]:

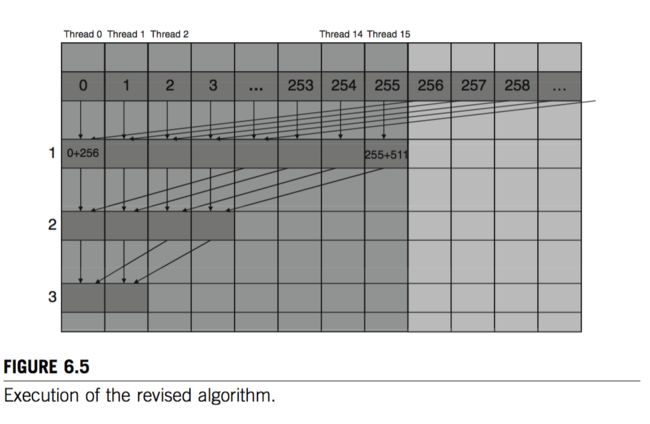
We can see that there is a if statement which will generate branch divergent. During the first iteration of the loop, only those threads whose threadIdx.x values are even will execute the add statement. One pass will be needed to execute these threads, and one additional pass will be needed to execute those that do not execute Line 8 [2]. In a warp, we have 32 threads. If we modify the code into this, we can get a better result[2]. 

Why?

For a section of 512 elements, threads 0 through 255 execute the add statement during the first iteration, while threads 256 through 511 do not. The pair-wise sums are stored in elements 0 through 255 after the first iteration. Because a warp consists of 32 threads with consecutive threadIdx.x values, all threads in warps 0 through 7 execute the add statement, whereas warps 8 through 15 all skip the add statement. Because all of the threads in each warp take the same path, there is no thread divergence![2]

The pattern is like this: 

Here is a ppt that worthwhile to have a look about branch divergent[1]. 

Except for the benefits of eliminating branch divergence, this version of code also make full use of the vector (the warp). Every thread in this warp is doing this calculation.

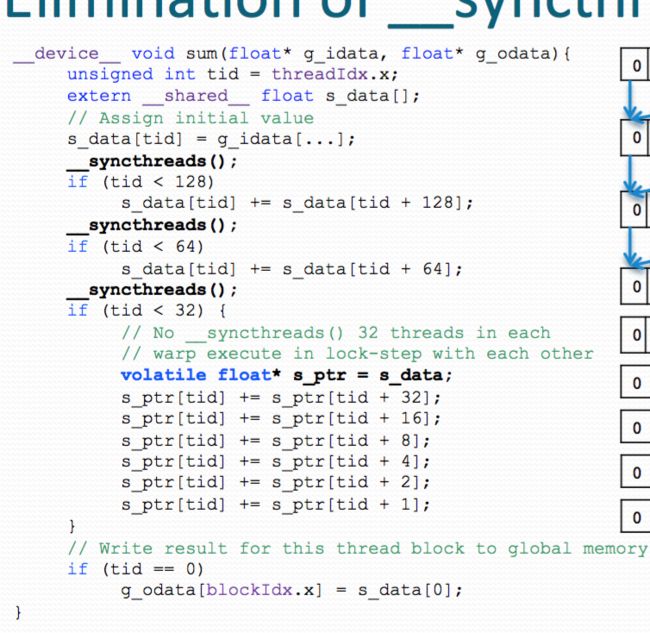
Additional Consideration: Eliminate the __syncthreads() [1]:

When there are less than 32 threads, we can sure they will in a warp. Then we can manually synchronise the threads. By resolve the code into several sentences like above. 

Consideration 2: Instruction Mix

Movtivation: In current-generation CUDA graphics processing units (GPUs), each processor core has limited instruction processing bandwidth. Every instruction consumes instruction processing bandwidth, whether it is a floating- point calculation instruction, a load instruction, or a branch instruction.[2]

We must try to let the floating- point calculation instruction occupy more portion of instruction processing bandwidth. 

The most common place to optimise is the for loop. 

For example[2]:

The loop incurs extra instructions to update loop counter k and performs conditional branch at the end of each iteration. Furthermore, the use of loop counter k to index the Ms and Ns matrices incurs address arithmetic instructions. These instructions compete against floating-point calculation instructions for the limited instruction processing bandwidth.[2]

With loop unrolling, given a tile size, one can simply unroll all the iterations and express the dot-product computation as one long multiply–add expression. This eliminates the branch instruction and the loop counter update. Furthermore, because the indices are constants rather than k, the compiler can use the addressing mode offsets of the load instructions to eliminate address arithmetic instructions.[2]

Those above are talking about loop unrolling manually. We can also do it automatically by using #pragma. 

Here is the rule[1]: 

How many times == tile size. 

Reference: 

1) CMU How to write fast code Jike Chong and Ian Lane

2) Programming.Massively.Parallel.Processors.A.Hands-on.Approach Kirk, Hwu