置换群幂运算
1.置换群中有一个定理:设T为一置换,e为单位置换,T^k=e,那么k的最小正整数解是T的拆分的所有循环长度的最小公倍数。
此定理用来解决Poj 2369Permutation
2.T^k将长度为L的置换T分裂成gcd(L,K)份,每个循环分别是循环T中下标i mod gcd(l,k)=0,1,2…的元素的连接。
单个循环置换幂运算:
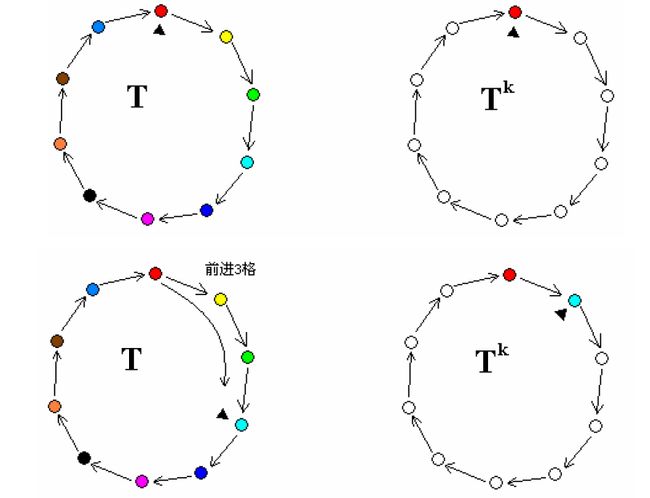
1、循环长度与指数互质时的整幂运算
设T=a,T^k=b,且gcd(L,k)=1,则b[i]=a[(k+1)*i%L]。由此可以构造出T^k(如L=10,k=3)
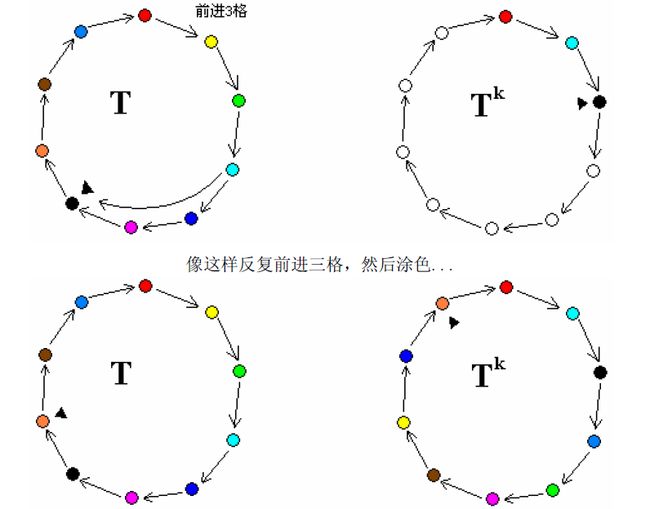
2、循环长度与指数互质的分数幂运算(开方)
构造方法与上述过程类似但互逆,不过就是目标循环每次指针向后移k位,源循环每次向后移1位罢了。
此算法可用于解决poj1721
3、循环长度与指数不互质时,单个循环是不能开方的。
多个循环的幂运算
1.整数幂运算:(p1 p2 p3...pn)^k=(p1)^k (p2)^k...(pn)^k不同循环节独立运算,整数次幂运算一定产生分裂效果。
例:poj3281 Leonardo's Notebook判断一个置换是否是一个置换平方后的结果,对于给出的置换,长度为偶数的循环节一定是由分裂产生的,因此必须成对出现,对于长度为奇数的循环节可能由于分裂产生也可能在原置换中独立存在,因此只要考虑偶置换是否成对。
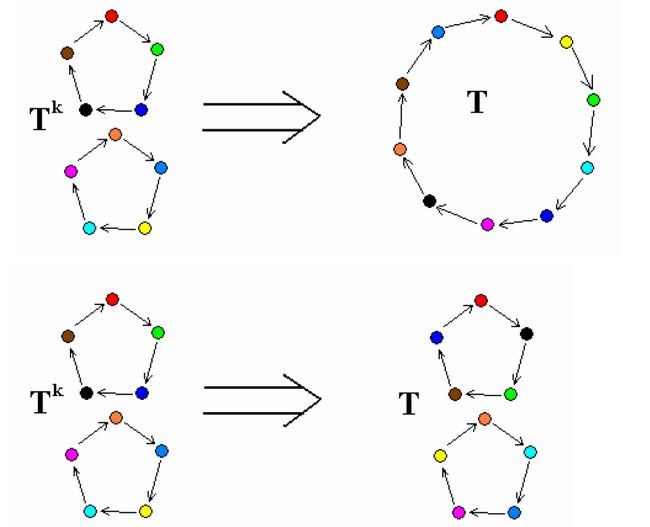
2、分数幂运算:在开方运算中,我们可以将k份相同长度l的循环依次交错地合并,作为一次开方的过程。因为这样一个长度k*L的循环,作k次幂运算,势必会分裂成这样的k份每份长度L的循环,所以这个做法是正确的。
将k个循环分别进行开方,得到的仍然是k个小循环,结果也是正确的。
定理:如果我们选择m个相同长度L的循环合并而作为一次运算过程的话,只要保证长度m*L的循环的k次方会把自己分裂为m份,就可以保证这个做法是正确的了。即:gcd(m*L,k)=m。
m是k的因数,并且gcd(L,k/m)=1。显然,这个式子的充分条件是m是gcd(L,k)的倍数
算法:较整幂运算来说,分数幂运算(开方)就比较复杂了,需要分好几种情况,解也不是唯一的。整理提供一个能求出一个正确解的O(n)算法
1. m=gcd(L,k)
2. 选择n*m份长度为L的循环交错合并,n为正整数,且gcd(n*m,k/m)=1(保证第三步可行)
3. 将大循环开k/m次方
置换连乘:
题目链接:VOJ1049
题目大意:顺次给出m个置换,反复使用这m个置换对初始序列进行操作,问k次置换后的序列。m<=10, k<2^31。
首先将这m个置换“合并”起来(算出这m个置换的乘积),然后接下来我们需要执行这个置换k/m次(取整,若有余数则剩下几步模拟即可)。注意任意一个置换都可以表示成矩阵的形式。例如,将1 2 3 4置换为3 1 2 4,相当于下面的矩阵乘法:
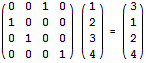
置换k/m次就相当于在前面乘以k/m个这样的矩阵。我们可以二分计算出该矩阵的k/m次方,再乘以初始序列即可。做出来了别忙着高兴,得意之时就是你灭亡之日,别忘了最后可能还有几个置换需要模拟。
ps:大量参考和引用 潘震皓《置换群快速幂运算 研究与探讨》,具体实例及证明请参考原文。