LCA（最近公共祖先）问题 （一）

最近共祖先

对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。
另一种理解方式是把T理解为一个无向无环图，而LCA(T,u,v)即u到v的最短路上深度最小的点。

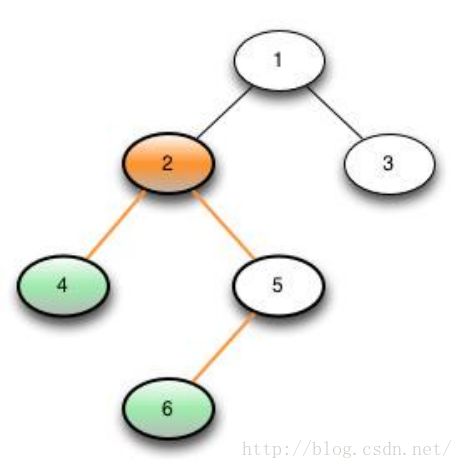
例如，对于下面的树，结点4和结点6的最近公共祖先LCA(T,4,6)为结点2。

方法（一）逐个向上找

直接暴力， 求A、B的LCA，可以以先以A为起点向上搜索，标记路过的点。然后从B再次搜索，当遇到第一个标记的点即为所求。不过复杂度。。呵呵。。

稍微好一点的优化是

首先计算出结点u和v的深度d1和d2。如果d1>d2，将u结点向上移动d1-d2步，如果d1<d2，将v结点向上移动d2-d1步，现在u结点和v结点在同一个深度了。下面只需要同时将u，v结点向上移动，直到它们相遇（到达同一个结点）为止，相遇的结点即为u，v结点的最小公共祖先。 
该算法时间复杂度为O(h)，对于多次询问的题目不能解决。

方法（二）倍增法

倍增法其实是在上一种方法的基础上进行了优化，我们希望向上查找更快，可以事先预处理出p[i,j]，表示i往上移动2^j步到达的结点，这样在查找时将大大节约时间。
由定义有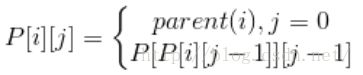
利用P数组可以快速的将结点i向上移动n步，方法是将n表示为2进制数。比如n=6，二进制为110，那么利用P数组先向上移动4步(2^2)，然后再继续移动2步(2^1)，即P[ P[i][2] ][1]。 

首先预处理出所有的p[i][j],并计算每个点的深度d[i]:

void dfs(int u,int fa)//从根结点u开始dfs，u的父亲是fa{ 
	d[u]=d[fa]+1; //u的深度为它父亲的深度+1
	p[u][0]=fa; //u向上走2^0步到达的结点是其父亲
	for(int i=1;i<=20;i++) p[u][i]=p[p[u][i-1]][i-1];//预处理p时，保证能从u走到p[u][i]
	for(int i=head[u];i!=-1;i=e[i].next)//对于u的每个儿子{ 
int v=e[i].v; 
		if(v!=fa)dfs(v,u); //递归处理以v为根结点的子树} 
} 

在主函数中调用dfs(1,0)即可

（下面的f就是上面的p数组=。=）

接下来是查询结点a,b的LCA
int lca(int a,int b)
{
	if(d[a] > d[b]) swap(a , b) ; //保证a点在b点上面
	for(int j = 20 ; j >= 0 ; j--) //将b点向上移动到和a的同				       一深度
		   if(d[a] <= d[b] - (1<<j)) b = f[b][j] ;
	if(a == b) return a ;//如果a和b相遇
	for(int j = 20 ; j >= 0 ; j--)//a,b同时向上移动
	 {
		   if(f[a][j] == f[b][j]) continue ;//如果a,b的2^j祖先相					    同，则不移动
		   a = f[a][j] , b = f[b][j] ;//否则同时移动到2^j处
	 }
	 return f[a][0] ;//返回最后a的父亲结点
}

时间复杂度分析
预处理：对每一个结点找到它向上走2^logN步到达的点，所以时间是NlogN
询问：logN
所以总复杂度为NlogN+QlogN

待续。。

ps：在下一节中将讲如何把LCA问题转化为RMQ问题并且会有一种更优的做法。