单源最短路径整理

Dijkstra算法

详解（http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html）

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

 

2.算法描述

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

 

执行动画过程如下图

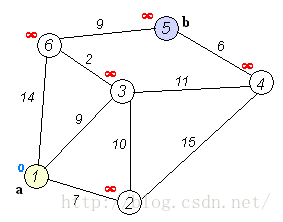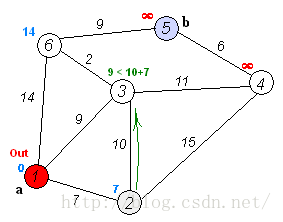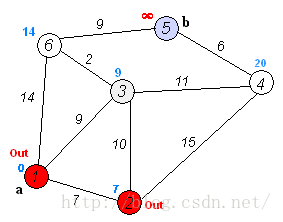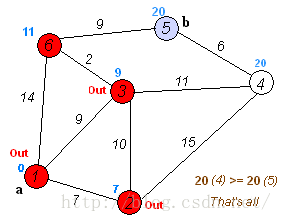
1、单源Dijkstra 

#define MAX 1010
#define INF 0x3f3f3f3f
bool vis[MAX];
int pre[MAX] ;  ///记录到当前点的父节点，用来还原路径

///注意开始输入的时候如果不能到达的应该初始化为INF

void Dijkstra (int cost[][MAX] , int lowcost[],int n,int beg)
{
    for(int i = 0 ; i<n ; i++)
        lowcost[i]=INF,vis[i]=false,pre[i]=-1;

    lowcost[beg] = 0;  ///设置起始 地点
    for(int j=0; j<n; j++)
    {
        int k=-1,Min = INF;
        for( int i=0 ; i<n ; i++ )  ///找出最小的lowcost
            if( !vis[i] && lowcost[i]<Min )
                Min=lowcost[i],k=i;
        if(k==-1) break;  ///如果在这里满足了，说明图不连通，还有一部分点未能到达
        vis[k] = true;
        for(int i = 0 ; i < n ; i++)
            if( !vis[i] && lowcost[k]+cost[k][i]<lowcost[i] )
              lowcost[i]=lowcost[k]+cost[k][i],pre[i]=k;
    }
}

2、Dijkstra算法+堆优化

运用优先队列，原理和最基本的Dijkstra相同

#define MAX 1000010
#define INF 0x3f3f3f3f
struct qnode
{
    int v,c;  ///分别记录当前节点下标和到当前点的最小花费
    qnode(int _v=0,int _c=0):v(_v),c(_c) {}  ///构造函数？？？
    bool operator < (const qnode &r) const
    {
        return c>r.c;
    }
};

struct Edge
{
    int v,cost;
    Edge(int _v=0,int _cost=0) : v(_v),cost(_cost) {}
};

vector <Edge> E[MAX];
bool vis[MAX];
int lowcost[MAX];

///点编号从1开始
void Dijkstra(int n,int start)
{
    memset(vis,false,sizeof(vis));
    for(int i = 1 ; i<=n ; i++)  lowcost[i] = INF;
    priority_queue <qnode> que;  ///优先队列存储已经能够到达的点
    while(!que.empty()) que.pop();
    ///que.clear();
    lowcost[start] = 0;
    que.push( qnode(start,0) );
    qnode temp;
    while(!que.empty()){
        temp = que.top();
        que.pop();
        int u=temp.v;
        if(vis[u]) continue;  ///由于不断更新，一个点可能多次压到队列中
        vis[u] = true;
        for(int i=0 ; i<E[u].size();i++){
            int v=E[u][i].v , cost = E[u][i].cost;
            if( !vis[v] && lowcost[v]>lowcost[u]+cost ){
                lowcost[v] = lowcost[u]+cost;
                que.push(qnode(v,lowcost[v]));
            }
        }
    }
}

3、SPFA算法

SPFA算法。（我不打算提Bellman-Ford算法，因为完全可以把SPFA当作Bellman-Ford的一种优化、变形以及竞赛中的替代品。）同样是用来解决单源最短路，图中可以有负权的边。使用一个队列，首先使源点入队，然后每次出队一个顶点，用这个顶点的当前距离更新它的所有邻接点的距离，所有距离实际上被更新且未在队列中的点入队。重复以上过程直至队列空。另外，当一个点入队次数超过图的顶点数时，表明图中存在负权环。SPFA的最坏情况，也就是图中有负权环时的时间复杂度是Θ(n*E)，但在实际应用中若没有负权环时会非常快，甚至可以认为大约与O(E)同阶。我在用到SPFA时一般都采用边表来来存边，这样可以最大限度发挥SPFA的优越性。点数较多而且边数较少时使用。竞赛中使用最频繁，往往考察对spfa算法的改造。或者多约束条件的spfa算法。

#include <iostream>
#include <stdio.h>
#include <queue>
#include <algorithm>
#include <string>
#include <string.h>
using namespace std;
#define MAX 1010
#define INF 0x3f3f3f3f

struct Edge
{
    int v,cost;
    Edge(int _v=0,int _cost=0) : v(_v),cost(_cost) {}
};

vector <Edge> E[MAX];   ///多组输入数据时注意清空
bool vis[MAX];  ///是否在队列中标志
int cnt [MAX];  ///如队列次序
int lowcost[MAX];
queue <int>que;


void addedge(int u,int v,int w){
  E[u].push_back(Edge(v,w));
}
void ini(int n){
    memset(vis,false,sizeof(vis));
    memset(cnt,0,sizeof(cnt));
    while(!que.empty()) que.pop();
    for(int i = 1 ; i<=n ; i++)
        lowcost[i] = INF;
}
///点编号从1开始
bool SPFA(int n,int start)
{
    ini(n);
    vis[start] = true;
    lowcost[start] = 0;
    cnt[start] = 1;

    que.push(start);

    while(!que.empty()){
        int u = que.front();  ///
        que.pop();

        vis[u] = false;

        for(int i=0 ; i<E[u].size() ; i++){
            int v=E[u][i].v ;
            if( lowcost[v] > lowcost[u] + E[u][i].cost ){
                lowcost[v] = lowcost[u] + E[u][i].cost;
                if(!vis[v]){     ///未出现在队列中
                    vis[v] = true;
                    que.push(v); ///只有到当前点出现更短的路径，并且当前点没有添加到队列中的时候才会添加到队列中再次遍历其孩子
                    if( ++cnt[v] > n ) return false; ///cnt[i] 为入队列次数 ，用来判断是否存在负环回路（原理？？？）
                }
            }
        }
    }
    return true;
}
int main (){
int T,n;
int u,v,w,tmp;
int start[MAX];
bool mark = 0;
while(~scanf("%d",&T)){
    n=-1;
    for(int i=1;i<MAX;i++) E[i].clear();

    for(int i=0;i<T;i++){
       mark = 0;
       scanf("%d%d%d",&u,&v,&w);
       for(int j=0;j<E[u].size();j++){    ///注意去除重边！！！！
          if(E[u][j].v == v){
            if(E[u][j].cost > w){
                E[u][j].cost = w , j=E[u].size();
             for(int k = 0 ; k <E[v].size() ; k++)
                if(E[v][j].v == u)
                    E[v][j].cost = w , k = E[v].size();
            }
            mark = 1;
          }
       }
      if(mark == 0){
         addedge(u,v,w);
         addedge(v,u,w);
         if(n<u) n=u;
         if(n<v) n=v;
      }
    }
    SPFA(n,1);
}
return 0;
}