hdu 2155（dp）

小黑的镇魂曲

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Problem Description

这个事情发生在某一天，当小黑和SSJ正在约会的时候，邪恶的Guner抓走了SSJ，小黑伤心万分，怒不可遏啊！但是他显然也是没有办法的，谁叫Guner比小黑邪恶，小黑打不过Guner呢！
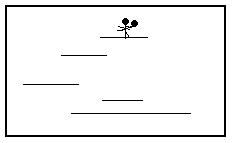
于是，小黑利用皮肤保护色，趁夜摸黑前往Guner的城堡，准备偷偷摸摸的把SSJ拯救出来，但是只要小黑一打开SSJ身上的锁链，看门的葱头就会在M秒以内通知Guner，Guner马上超时空转移，闪到小黑身边抓住他们，于是小黑虽然跑得不快，但是他也不得不跑啊。
由于Guner的城堡构造特殊，它是由一个一个的平台搭建成的，所以小黑的逃跑路线是这样的，在时刻0的时候，他位于最高点，也就是高于所有的平台，然后他开始垂直下落，他的下落速度是1米/秒。当小黑下落到某个平台上时，他可以向左跑也可以向右跑，他的跑动速度还是1米/秒。当小黑又处于平台边缘的时候，他开始继续下落。但是小黑是个怜香惜玉的人，为了顾及怀中的SSJ，于是他每次下落的最大高度不会超过MAX米，不然SSJ摔坏了，Guner也懒得追了，小黑也会伤心致死的。但是只要小黑抱着SSJ一落到地面，Guner就再也抓不住他们了。

 

Input

第一行输入一个数T(0 < T <= 10)，表示测试数据的组数。每组测试数据的第一行是5个整数，N,X,Y,MAX,M,用空格分开。N(0 < N <= 1000)是台阶的数目，X,Y分别是小黑0时刻所在位置的横、纵坐标，MAX表示小黑最多能下落的高度，M表示从小黑一打开锁链葱头发觉后报告给Guner的时间，接下来有N行数据，每行数据描述一个台阶，包括3个数据，Xl[i],Xr[i],H[i],其中Xl[i](0 < Xl[i] <= 1000)表示当前台阶最左边的边的X坐标，Xr[i](0 < Xr[i] <= 1000)表示当前台阶最右边的边的X坐标，H[i](0 < H[i] < 1000)表示当前台阶离地面的高度。数据确保小黑和SSJ是能到达地面的。

 

Output

每组测试数据当Guner能抓住小黑和SSJ时，输出YES，否则输出NO.

 

Sample Input

   
   
   
   

    
    
    
    1
1 10 17 20 20
1 8 7
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    NO
   
   
   
   
   
   
   
   


   
   
   
   
   
   
   
   

    
    
    
    解题思路：这道题目是一个比较明显的DP，这里把整个平面看成一个二维坐标系，那么就很好列出状态方程，设dp[i][j]为到坐标为（i，j）的点时，所需要最短的时间（其实就是走的距离）。那么状态方程就是：dp[xr][j-k] = min{dp[i][j]+k+xr-i},dp[xl][j-k] = min{dp[i][j]+k+i-xl} (表示从(i,j)处落下，到台阶两侧的距离)。k是从1-MAX枚举的，表示落下的高度是k。那么这个算法就需要三层循环，最外面两层枚举坐标点，最里面一层从1-MAX枚举下落的高度。。此外，这里在判断某一个高度时是否有台阶可以降落，可以用hash来记录。。。
   
   
   
   
   
   
   
   

    
    
    
     
   
   
   
   
   
   
   
   

    
    
    
    AC:
   
   
   
   
   
   
   
   

    
    
    
    
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

const int maxn = 1005;
const int inf = 0x3f3f3f3f;
int n,m,x,y,MAX,cnt,minx,maxx;
int dp[maxn][maxn],h[maxn];
struct Node
{
	int xl,xr,h;
	int next;
}node[maxn];

void init()
{
	memset(dp,-1,sizeof(dp));
	memset(h,-1,sizeof(h));
	cnt = 0;
	minx = inf;
	maxx = 0;
}

void add(int XL,int XR,int H)
{
	int t = h[H];
	node[cnt].xl = XL;
	node[cnt].xr = XR;
	node[cnt].h = H;
	node[cnt].next = -1;
	if(t == -1)
		h[H] = cnt++;
	else
	{
		node[cnt].next = t;
		h[H] = cnt++;
	}
}

int search(int H,int X) //返回节点编号
{
	int t = h[H];
	while(t != -1)
	{
		if(node[t].xl <= X && node[t].xr >= X)
			return t;
		t = node[t].next;
	}
	return -1;
}

void solve()
{
	//先找到落在的第一块板上
	int hei;
	for(hei = 0; hei <= MAX; hei++)
	{
		int t = search(y-hei,x);
		if(t != -1)
		{
			dp[node[t].xl][y-hei] = hei + x-node[t].xl;
			dp[node[t].xr][y-hei] = hei + node[t].xr - x;
			break;
		}
	}
	for(int j = y-hei; j >= 0; j--)
		for(int i = maxx; i >= minx; i--)
			for(int k = 1; k <= MAX; k++)
			{
				if(dp[i][j] == -1) break;
				if(j - k == 0)
				{
					dp[i][0] = dp[i][j] + k;
					break;
				}
				int t = search(j-k,i);
				if(t == -1) continue;
				if(dp[node[t].xl][j-k] == -1)
					dp[node[t].xl][j-k] = dp[i][j] + k + i - node[t].xl;
				else dp[node[t].xl][j-k] = min(dp[node[t].xl][j-k],dp[i][j] + k + i - node[t].xl);
				if(dp[node[t].xr][j-k] == -1)
					dp[node[t].xr][j-k] = dp[i][j] + k + node[t].xr - i;
				else dp[node[t].xr][j-k] = min(dp[node[t].xr][j-k],dp[i][j] + k + node[t].xr - i);
				break;
			}
	int ans = inf;
	for(int i = 0; i <= 1000; i++)
		if(dp[i][0] != -1)
			ans = min(ans,dp[i][0]);
	if(ans > m) cout<<"YES"<<endl;
	else cout<<"NO"<<endl;
}

int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		init();
		cin>>n>>x>>y>>MAX>>m;
		for(int i = 1; i <= n; i++)
		{
			int XL,XR,H;
			cin>>XL>>XR>>H;
			minx = min(minx,XL);
			maxx = max(maxx,XR);
			add(XL,XR,H);
		}
		solve();
	}
	return 0;
}