树的直径、树的重心与树的点分治

树的直径

树的直径(Diameter)是指树上的最长简单路。

直径的求法：两遍搜索 (BFS or DFS)

任选一点w为起点，对树进行搜索，找出离w最远的点u。

以u为起点，再进行搜索，找出离u最远的点v。则u到v的路径长度即为树的直径。

简单证明：

如果w在直径上，那么u一定是直径的一个端点。反证：若u不是端点，则从直径另一端点到w再到u的距离比直径更长，与假设矛盾。

如果w不在直径上，且w到其距最远点u的路径与直径一定有一交点c，那么由上一个证明可知，u是直径的一个端点。

如果w到最远点u的路径与直径没有交点，设直径的两端为S与T，那么(w->u)>(w->c)+(c->T)，推出(w->u)+(S->c)+(w->c)>(S->c)+(c->T)=(S->T)与假设矛盾。

因此w到最远点u的路径与直径必有交点。

S-----------c-----------T

                 |

                w------u

 

树的重心

何谓重心

树的重心：找到一个点，其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡。

树的重心可以通过简单的两次搜索求出，第一遍搜索求出每个结点的子结点数量son[u]，第二遍搜索找出使max{son[u],n-son[u]-1}最小的结点。

实际上这两步操作可以在一次遍历中解决。对结点u的每一个儿子v，递归的处理v，求出son[v]，然后判断是否是结点数最多的子树，处理完所有子结点后，判断u是否为重心。

struct CenterTree{
    int n;
    int ans;
    int siz;
    int son[maxn];
    void dfs(int u,int pa){
        son[u]=1;
        int res=0;
        for (int i=head[u];i!=-1;i=edges[i].next){
            int v=edges[i].to;
            if (v==pa) continue;
            if (vis[v]) continue;
            dfs(v,u);
            son[u]+=son[v];
            res=max(res,son[v]-1);
        }
        res=max(res,n-son[u]);
        if (res<siz){
            ans=u;
            siz=res;
        }
    }
    int getCenter(int x){
        ans=0;
        siz=INF;
        dfs(x,-1);
        return ans;
    }
}Cent;

还有一种方法，虽然不能保证求出来的一定是重心，但是能找到一个结点，而这个以这个结点为根的话，所有的子树的结点数量都不会超过总结点数的一半。

同样是先搜索出son[u]，从某个假设的根开始向下找，如果有子结点v，使son[v]>son[u]/2，就以v作为新的根，重复执行，直到没有满足条件的子结点。

 

【POJ 1655 Balancing Act】

给定一棵树，求树的重心的编号以及重心删除后得到的最大子树的节点个数，如果个数相同就选取编号最小的。

直接套模板可解，注意要取编号最小的根。

 

树的点分治

何谓分治

分治，指的是分而治之，即将一个问题分割成一些规模较小的相互独立的子问题，以便各个击破。

我们常见的是在一个线性结构上进行分治，而分治算法在树结构上的运用，称之为树的分治算法。

分治往往与高效联系在一起，而树的分治正是一种用来解决树的路径问题的高效算法。

树的点的分治：首先选取一个点将无根树转为有根树，再递归处理每一颗以根结点的儿子为根的子树。

首先我们考虑如何选取点。对于基于点的分治，我们选取一个点，要求将其删去后，结点最多的树的结点个数最小，这个点就是树的重心。

在基于点的分治中每次我们都会将树的结点个数减少一半，因此递归深度最坏是 O(NlogN) 的，在树是一条链的时候达到上界。

 

【例 POJ 1741 Tree】

给你一棵TREE,以及这棵树上边的距离。问有多少对点它们两者间的距离小于等于K。

我们知道一条路径要么过根结点，要么在一棵子树中，这启发了我们可以使用分治算法。

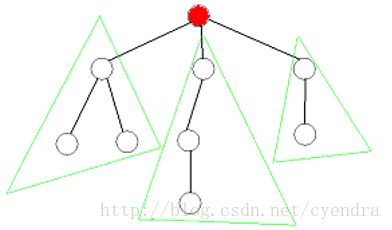
只要先求出经过根结点的路径数，再递归的求经过所有子结点的路径数即可。

下面来分析如何处理路径过根结点的情况。 

我们先用一次搜索求出根的所有子结点到根的距离并将其放入一个数组中，复杂度O(n)。

将这个距离数组排序，复杂度O(nlogn)。

这样就将问题转化为了，求一个数组A中，和小于等于K的元素对个数有多少。

由于数组有序，对于区间[L,R]，易知若A[L]+A[R]>K，那么区间内没有满足条件的元素对。若A[L]+A[R]<=K，则以L为左端点的点对数有R-L个。

我们从1开始枚举L，当前R不满足条件，就令R-1，否则统计以L为左端点的点对数，令L-1。

用一个线性扫描的扫描可以解决，复杂度O(n)。

最终我们得到了所有子结点到根的距离和小于等于K的点对数。

然而这个并不是最终解，因为我们要求的是经过根的路径，而从一个子树到达根结点又回到同一个子树的路径是不能被计入统计的，所以我们要把多余的点对从结果中减去。

我们只要对每一个子树，求出同一个子树中的结点到根结点又回到子树的路径和小于等于K的点对数，然后从答案中减去即可。 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=11000;
const int maxm=21111;
struct EdgeNode{
    int to;
    int w;
    int next;
}edges[maxm];
int head[maxn],edge;
bool vis[maxn];

void init(){
    edge=0;
    memset(head,-1,sizeof(head));
    memset(vis,0,sizeof(vis));
}
void addedge(int u,int v,int w){
    edges[edge].w=w,edges[edge].to=v,edges[edge].next=head[u],head[u]=edge++;
}
int n,K;
struct CenterTree{
    int n;
    int ans;
    int siz;
    int son[maxn];
    void dfs(int u,int pa){
        son[u]=1;
        int res=0;
        for (int i=head[u];i!=-1;i=edges[i].next){
            int v=edges[i].to;
            if (v==pa) continue;
            if (vis[v]) continue;
            dfs(v,u);
            son[u]+=son[v];
            res=max(res,son[v]-1);
        }
        res=max(res,n-son[u]);
        if (res<siz){
            ans=u;
            siz=res;
        }
    }
    int getCenter(int x){
        ans=0;
        siz=INF;
        dfs(x,-1);
        return ans;
    }
}Cent;
int data[maxn];
int dis[maxn];
int Len;
int ans;
void getArray(int u,int pa){
    data[++Len]=dis[u];
    for (int i=head[u];i!=-1;i=edges[i].next){
        int v=edges[i].to;
        int w=edges[i].w;
        if (v==pa) continue;
        if (vis[v]) continue;
        dis[v]=dis[u]+w;
        getArray(v,u);
    }
}
int calc(int u,int now){
    dis[u]=now;
    Len=0;
    getArray(u,-1);
    sort(data+1,data+Len+1);
    int res=0;
    int l=1,r=Len;
    while (l<r){
        if (data[r]+data[l]<=K){
            res+=(r-l);
            l++;
        }
        else r--;
    }
    return res;
}
void solve(int u){
    ans+=calc(u,0);
    vis[u]=true;
    for (int i=head[u];i!=-1;i=edges[i].next){
        int v=edges[i].to;
        int w=edges[i].w;
        if (vis[v]) continue;
        ans-=calc(v,w);
        Cent.n=Cent.son[v];
        int rt=Cent.getCenter(v);
        solve(rt);
    }
}
int main()
{
    while (~scanf("%d%d",&n,&K)){
        if (n==0&&K==0) break;
        init();
        for (int i=1;i<n;i++){
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            addedge(x,y,z);
            addedge(y,x,z);
        }
        ans=0;
        Cent.n=n;
        int root=Cent.getCenter(1);
        solve(root);
        printf("%d\n",ans);
    }
    return 0;
}
/**
20 10
1 2 3
2 3 4
3 4 5
4 5 6
5 6 7
6 7 8
7 8 9
8 9 10
9 10 11
10 11 12
11 12 13
12 13 14
13 14 15
14 15 16
15 16 17
16 17 18
17 18 19
18 19 20
19 20 21
**/