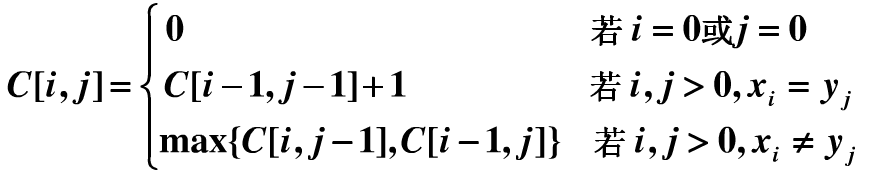最长公共子序列LCS和字符串编辑距离
最长公共子序列问题是求两个字符串中出现的相同的有先后次序的字符集合(可以不连续),连续的公共子序列是公共子串问题。
参考 http://www.cnblogs.com/huangxincheng/archive/2012/11/11/2764625.html
解决方案是动态规划算法,明白递推公式即可快速写出代码,动态规划算法就是解决子问题重叠的场景,不断利用子问题的最优解,所以一般会用到辅助矩阵来存储子问题最优解(空间复杂度O(M*N),可以优化到O(N))。本问题中,用矩阵C[m][n]存储,C[i][j]表示子串Xi和子串Yj的最长公共子序列长度。
Java实现的代码如下:
/**
* 使用动态规划法求解两个字符串str1和str2的最长公共子序列
* 搜索的时间复杂度O(M*N),辅助矩阵O(M*N),回溯输出的时间复杂度为O(M+N)
* 公共子序列可以不是连续的串
* @author pixel
*
*/
public class LCS {
private static byte LEFT = 1;
private static byte UP = 2;
private static byte LU = 3;
private String str1;
private String str2;
private int matrix[][];
private byte direction[][];
private int longest = 0;
private String sequence = "";
/**
* 构造函数,必须传入两个字符串
* @param str1 字符串1
* @param str2 字符串2
*/
public LCS(String str1, String str2)
{
this.str1 = str1;
this.str2 = str2;
}
public void lcs()
{
if(str1 == null || str2 == null || str1.length() == 0 || str2.length() == 0)
return;
dp();
System.out.print("最长公共子序列为:");
sub(str1.length(), str2.length());
}
/**
* 返回最长公共子序列的长度
* @return longest 在此之前必须先调用lcs()计算,否则返回0
*/
public int getLongest()
{
return longest;
}
/**
* 返回最长公共子序列
* @return sequence 在此之前必须先调用lcs()计算,否则返回""
*/
public String getSequence()
{
return sequence;
}
private void dp()
{
matrix = new int[str1.length()+1][str2.length()+1];
direction = new byte[str1.length()+1][str2.length()+1];
//初始化,i=0 j=0时,最长公共子序列为0
for (int i = 0; i <= str1.length(); i ++)
matrix[i][0] = 0;
for (int i = 0; i <= str2.length(); i ++)
matrix[0][i] = 0;
//动态规划,不断利用子问题的最优结果
for (int i = 1; i <= str1.length(); i ++)
{
for (int j = 1; j <= str2.length(); j ++)
{
if (str1.charAt(i-1) == str2.charAt(j-1))
{
matrix[i][j] = matrix[i-1][j-1] + 1;
direction[i][j] = LU;
System.out.println("str1["+i+"]=str2["+j+"], direction=LU");
}
else
{
if (matrix[i][j-1] > matrix[i-1][j])
{
matrix[i][j] = matrix[i][j-1];
direction[i][j] = LEFT;
}
else
{
matrix[i][j] = matrix[i-1][j];
direction[i][j] = UP;
}
}
}
}
longest = matrix[str1.length()][str2.length()];
System.out.println("最长公共子序列长度为:" + longest);
}
/**
* 回溯输出公共子序列中的字符
* 时间复杂度为O(M+N)
* @param i 辅助矩阵中的行坐标
* @param j 辅助矩阵中的列坐标
*/
private void sub(int i, int j)
{
if (i == 0 || j == 0)
return;
if (direction[i][j] == LU)
{
sub(i - 1, j - 1);
System.out.print(str1.charAt(i-1));
sequence += str1.charAt(i-1);
}
else
{
if (direction[i][j] == UP)
{
sub(i - 1, j);
}
else
{
sub(i, j - 1);
}
}
}
public static void main(String[] args)
{
String str1 = "cnblog";
String str2 = "belong";
LCS lcs = new LCS(str1, str2);
lcs.lcs();
System.out.println();
System.out.println(lcs.getLongest());
System.out.println(lcs.getSequence());
}
}
字符串编辑距离,或者说是字符串的相似度,和最长公共子序列问题类似。目的是通过增、删、改一个字符串,变成另一个字符串,要求所用的操作最少,这个操作次数就是这个字符串和另一个字符串的编辑距离。
解决方案还是用一个矩阵C[m][n]保存子问题的最优解,C[i][j]保存子串Xi与Yj的编辑距离,递推公式如下:
①:当 Xi = Yi 时,则C[i, j]=C[i-1, j-1];
②:当 Xi != Yi 时, 则C[i, j]=Min{C[i-1, j-1], C[i-1, j], C[i, j-1]};