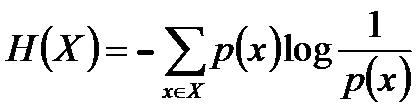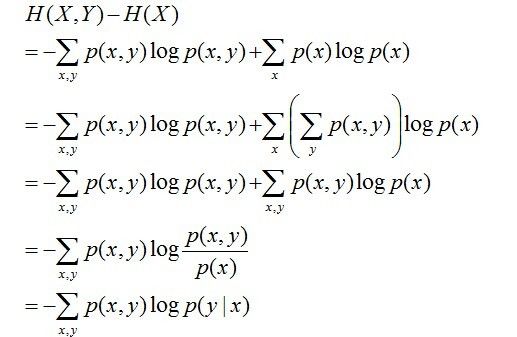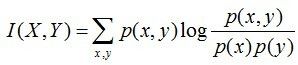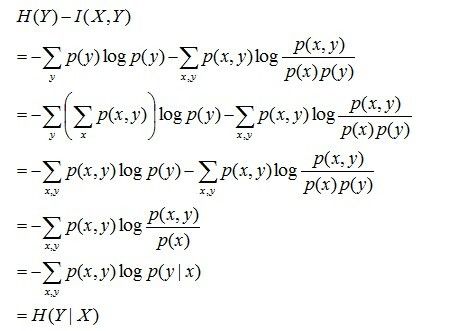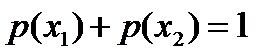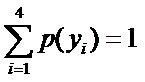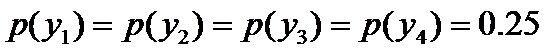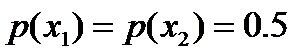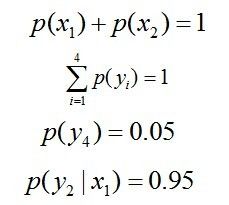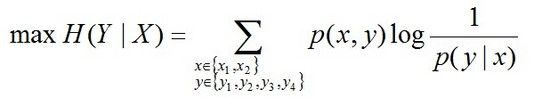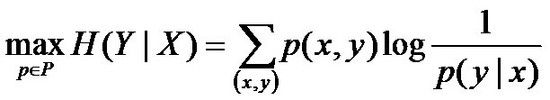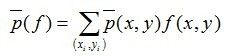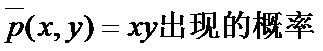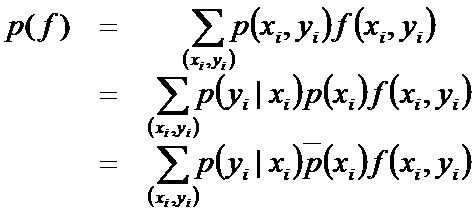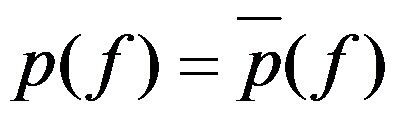最大熵模型中的数学推导

最大熵模型中的数学推导

引言

写完SVM之后，早就想继续写机器学习的系列，无奈一直时间不稳定且对各个模型算法的理解尚不够，所以一直迟迟未动笔。无独有偶，重写KMP得益于今年4月个人组织的算法班，而动笔继续写这个机器学习系列，正得益于今年10月组织的机器学习班。

10月26日机器学习班第6次课，身为讲师之一的邹博讲最大熵模型，从熵的概念，讲到为何要最大熵、最大熵的推导，以及求解参数的IIS方法，整个过程讲得非常流畅，特别是其中的数学推导。晚上我把他的PPT 在微博上公开分享了出来。但对于没有上过课的朋友直接看PPT 会感到非常跳跃，因此我打算针对机器学习班的某些次课写一系列博客，刚好也算继续博客中未完的机器学习系列，何乐而不为呢？

综上，本文结合我的搭档邹博最大熵模型的PPT和其它相关资料写就，可以看成是课程笔记或学习心得，希望可以写成之前那篇SVM一样，虽尚不完美但足够通俗易懂。有何建议或意见，欢迎随时于本文评论下指出，thanks。

1 何谓熵？

从名字上来看，熵给人一种很玄乎，不知道是啥的感觉。其实，熵的定义很简单，即用来表示随机变量的不确定性。之所以给人玄乎的感觉，大概是因为为何要取这样的名字，以及怎么用。

熵的概念最早起源于物理学，用于度量一个热力学系统的无序程度。在信息论里面，熵是对不确定性的测量。但是在信息世界，熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。

1.1 熵的引入

事实上，熵的英文原文为entropy，最初由德国物理学家鲁道夫·克劳修斯提出，

表示一個系統在不受外部干扰时，其内部最稳定的状态。后来一中国学者翻译entropy时，考虑到entropy是能量Q跟温度T的商，且跟火有关，便把entropy形象的翻译成熵。

我们知道，任何粒子的常态都是随机运动，也就是"无序运动"，如果让粒子呈现"有序化"，必须耗费能量。所以，能量可以被看作"有序化"的一种度量，而"熵"可以看作是"无序化"的度量。

如果没有外部能量输入，封闭系统趋向越来越混乱（熵越来越大）。比如，如果房间无人打扫，不可能越来越干净（有序化），只可能越来越乱（无序化）。而要让一个系统变得更有序，必须有外部能量的输入。

1948年，香农Claude E. Shannon把信息（熵）定义为离散随机事件的出现概率。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。所以，信息熵也可以说是系统有序化程度的一个度量。 若无特别指出，下文中所有提到的熵均为信息熵。

1.2 熵的定义

下面分别给出熵、联合熵、条件熵、相对熵、互信息的定义。

熵 ：如果一个随机变量X的可能取值为X={x1, x2,…, xk}，其概率分布为P(X = xi) = pi（i = 1,2, ..., n），则随机变量X的熵定义为：

联合熵 ：两个随机变量X，Y的联合分布，可以形成联合熵Joint Entropy，用H(X,Y)表示。

条件熵 ：在X发生的前提下，Y发生所“新”带来的熵定义为Y的条件熵，用H(Y|X)表示。且有此式子成立：H(Y|X) = H(X,Y) – H(X)，整个式子表示(X,Y)发生所包含的熵，减去X单独发生包含的熵。至于怎么来的请看推导：

相对熵： 又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布，则p对q的相对熵是

在一定程度上，相对熵可以度量两个随机变量的“距离”，且有D(p||q) ≠D(q||p)。

互信息 ：两个随机变量X，Y的互信息，定义为X，Y的联合分布和独立分布乘积的相对熵，用表示I(X,Y)

且有I(X,Y)=D(P(X,Y) || P(X)P(Y))。下面，咱们来计算下H(Y)-I(X,Y)的结果，如下：

通过上面的计算过程，我们发现竟然有H(Y)-I(X,Y) = H(Y|X)。故通过条件熵的定义，有：H(Y|X) = H(X,Y) - H(X)，而根据互信息定义展开得到H(Y|X) = H(Y) - I(X,Y)，把前者跟后者结合起来，便有I(X,Y)= H(X) + H(Y) - H(X,Y)，此结论被多数文献作为互信息的定义。

2 最大熵

熵是随机变量不确定性的度量，不确定性越大，熵值越大；若随机变量退化成定值，熵为0。如果没有外界干扰，随机变量总是最大程度的趋向于无序，所以它的熵总是比较大的。

为了准确的估计随机变量的状态，我们一般习惯性最大化熵，其原则是承认已知事物（知识），且对未知事物不做任何假设，没有任何偏见。

2.1 无偏原则

下面举个大多数有关最大熵模型的文章中都喜欢举的一个例子。

一篇文章中出现了“学习”这个词，那这个词是主语、谓语、还是宾语呢？换言之，已知“学习”可能是动词，也可能是名词，故“学习”可以被标为主语、谓语、宾语、定语等等。

• 令x1表示“学习”被标为名词， x2表示“学习”被标为动词。
• 令y1表示“学习”被标为主语， y2表示被标为谓语， y3表示宾语， y4表示定语。

且假设已有：   ， ， 则根据无偏原则，可得到：

进一步，若已知：“学习”被标为定语的可能性很小，只有0.05，即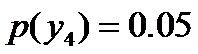，此时依然根据无偏原则，可得：

当“学习”被标作动词的时候，它被标作谓语的概率为0.95，即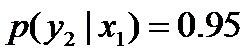，此时仍然需要坚持无偏见原则，使得概率分布尽量平均。但怎么样才能得到尽量无偏见的分布？

事实上，概率平均分布  等价于  熵最大。于是，问题便转化为了：计算X和Y的分布，使得H(Y|X)达到最大值，并且满足下述条件：

故要最大化下述式子：

且满足以下4个约束条件：

2.2 最大熵模型

至此，我们可以写出最大熵模型的一般表达式了，如下：

其中，P={p | p是X上满足条件的概率分布}

继续阐述之前，先定义下特征、样本和特征函数。

特征：(x,y)

• y：这个特征中需要确定的信息
• x：这个特征中的上下文信息

样本：关于某个特征(x,y)的样本，特征所描述的语法现象在标准集合里的分布：(xi,yi)对，其中，yi是y的一个实例，xi是yi的上下文。

对于一个特征(x0,y0)，定义特征函数：

特征函数关于经验分布  在样本中的期望值是：

表示的是(x,y)在样本中出现的概率。其中，。

假设样本的分布已知，则对每一个特征(x,y)，模型所建立的条件概率分布要与训练样本表现出来的分布相同。

如果能够获取训练数据中的信息，那么上述这两个期望值相等，即：

参考文献

1. 热力学熵http://zh.wikipedia.org/zh-mo/%E7%86%B5，信息熵：http://zh.wikipedia.org/zh-mo/%E7%86%B5，百度百科：http://baike.baidu.com/view/401605.htm；
2. 熵的社会学意义：http://www.ruanyifeng.com/blog/2013/04/entropy.html；
3. 北京10月机器学习班邹博的最大熵模型PPT： http://pan.baidu.com/s/1qWLSehI；