二叉树的深度优先搜索和广度优先搜索

深度优先搜索算法（Depth First Search），是搜索算法的一种。是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。

当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。

如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

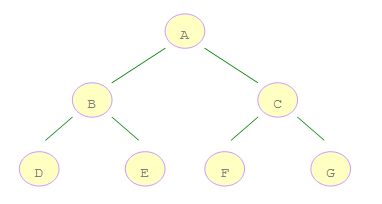
如右图所示的二叉树：

A 是第一个访问的，然后顺序是 B、D，然后是 E。接着再是 C、F、G。

那么，怎么样才能来保证这个访问的顺序呢？

分析一下，在遍历了根结点后，就开始遍历左子树，最后才是右子树。

因此可以借助堆栈的数据结构，由于堆栈是后进先出的顺序，由此可以先将右子树压栈，然后再对左子树压栈，

这样一来，左子树结点就存在了栈顶上，因此某结点的左子树能在它的右子树遍历之前被遍历。

深度优先遍历代码片段

  
// 深度优先遍历
void  depthFirstSearch(Tree root){
    stack < Node  *>  nodeStack;   // 使用C++的STL标准模板库
    nodeStack.push(root);
    Node  * node;
     while ( ! nodeStack.empty()){
        node  =  nodeStack.top();
        printf(format, node -> data);   // 遍历根结点
        nodeStack.pop();
         if (node -> rchild){
            nodeStack.push(node -> rchild);   // 先将右子树压栈
        }
         if (node -> lchild){
            nodeStack.push(node -> lchild);   // 再将左子树压栈
        }
    }
}
  

广度优先搜索算法（Breadth First Search），又叫宽度优先搜索，或横向优先搜索。

是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

如右图所示的二叉树，A 是第一个访问的，然后顺序是 B、C，然后再是 D、E、F、G。

那么，怎样才能来保证这个访问的顺序呢？

借助队列数据结构，由于队列是先进先出的顺序，因此可以先将左子树入队，然后再将右子树入队。

这样一来，左子树结点就存在队头，可以先被访问到。

广度优先遍历代码片段

  

//广度优先遍历
void breadthFirstSearch(Tree root){
    queue<Node *> nodeQueue;  //使用C++的STL标准模板库
    nodeQueue.push(root);
    Node *node;
    while(!nodeQueue.empty()){
        node = nodeQueue.front();
        nodeQueue.pop();
        printf(format, node->data);
        if(node->lchild){
            nodeQueue.push(node->lchild);  //先将左子树入队
        }
        if(node->rchild){
            nodeQueue.push(node->rchild);  //再将右子树入队
        }
    }
}
  

完整代码:

  

/**
 * <!--
 * File   : binarytree.h
 * Author : fancy
 * Email  : [email protected]
 * Date   : 2013-02-03
 * --!>
 */
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <Stack>
#include <Queue>
using namespace std;
#define Element char
#define format "%c"

typedef struct Node {
    Element data;
    struct Node *lchild;
    struct Node *rchild;
} *Tree;

int index = 0;  //全局索引变量

//二叉树构造器,按先序遍历顺序构造二叉树
//无左子树或右子树用'#'表示
void treeNodeConstructor(Tree &root, Element data[]){
    Element e = data[index++];
    if(e == '#'){
        root = NULL;
    }else{
        root = (Node *)malloc(sizeof(Node));
        root->data = e;
        treeNodeConstructor(root->lchild, data);  //递归构建左子树
        treeNodeConstructor(root->rchild, data);  //递归构建右子树
    }
}

//深度优先遍历
void depthFirstSearch(Tree root){
    stack<Node *> nodeStack;  //使用C++的STL标准模板库
    nodeStack.push(root);
    Node *node;
    while(!nodeStack.empty()){
        node = nodeStack.top();
        printf(format, node->data);  //遍历根结点
        nodeStack.pop();
        if(node->rchild){
            nodeStack.push(node->rchild);  //先将右子树压栈
        }
        if(node->lchild){
            nodeStack.push(node->lchild);  //再将左子树压栈
        }
    }
}

//广度优先遍历
void breadthFirstSearch(Tree root){
    queue<Node *> nodeQueue;  //使用C++的STL标准模板库
    nodeQueue.push(root);
    Node *node;
    while(!nodeQueue.empty()){
        node = nodeQueue.front();
        nodeQueue.pop();
        printf(format, node->data);
        if(node->lchild){
            nodeQueue.push(node->lchild);  //先将左子树入队
        }
        if(node->rchild){
            nodeQueue.push(node->rchild);  //再将右子树入队
        }
    }
}
  

 

二叉树的深度优先遍历（中序遍历）：

当我们利用树的深度优先遍历找到满足条件的一条路径时，需要设置一个bool类型标志，如果在左子树中已经找到，则不需递归右子树，一般采用以下步骤：

Bool findPath(pCur,pNode)
If(满足条件)
Return true;
s.push(pcur);
Bool found=false;//设置一个标志，来判断是否已经找到了一条路径
If(pCur->left)
   found=findPath(pCur->left,pNode);
If(pCur->right && !found) //找到了就不用递归
   found=findPath(pCur->right,pNode);
If(!found)
     s.pop();
Return found;
当我们需要找到所有满足条件的路径时，一般采用如下步骤：
Void findPath(pcur,pnode)
If(满足条件)
Print;
更新状态;
s.push(pcur);
If(pcur->left)
Findpath(pcur->left,pnode);
If(pcur->right)
Findpath(pcur->right,pnode);
还原添加此节点时的状态;
s.pop();